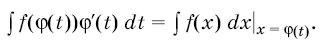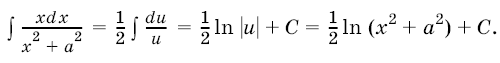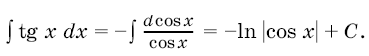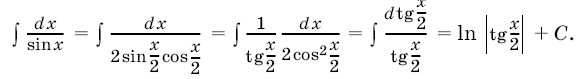Участник:Пасконова Ольга/Песочница
Материал из MachineLearning.
(→Формула замены переменных в неопределенном интеграле) |
(→Формула замены переменных в неопределенном интеграле) |
||
| Строка 19: | Строка 19: | ||
::[[Изображение:Q3.png]] | ::[[Изображение:Q3.png]] | ||
| - | то будет видно, что, для того чтобы вычислить интеграл [[Изображение:Q4.png]]), можно сделать подстановку <tex> х = \phi( | + | то будет видно, что, для того чтобы вычислить интеграл [[Изображение:Q4.png]]), можно сделать подстановку <tex> х = \phi(t) <tex>, вычислить интеграл <tex> \int f(x) dx </tex> и затем вернуться к переменной <tex> t <tex>, положив <tex> х = \phi(t) <tex>. |
'''Примеры.''' | '''Примеры.''' | ||
| - | 1 | + | '''1.''' Для вычисления интеграла <tex> \int cos ax dx </tex> естественно сделать подстановку <tex> u = ах </tex>, тогда |
| - | + | ||
| - | + | ::[[Изображение:Q5.png]] | |
| - | 2. Для вычисления интеграла | + | |
| - | + | '''2.''' Для вычисления интеграла [[Изображение:Q6.png]] удобно применить подстановку | |
| - | 3 | + | <tex> u = x^3 + a^3 </tex>: |
| - | + | ||
| + | ::[[Изображение:Q7.png]] | ||
| - | 3. При вычислении интегралов вида | + | '''3.''' При вычислении интегралов вида [[Изображение:Q8.png]] полезна подстановка |
| - | + | <tex> u = \phi(х) </tex>: | |
| + | ::[[Изображение:Q9.png]] | ||
| + | Например, | ||
| + | ::[[Изображение:Q10.png]] | ||
| - | Иногда, прежде чем применить метод интегрирования подстановкой, приходится проделать более сложные | + | Иногда, прежде чем применить метод интегрирования подстановкой, приходится проделать более сложные преобразования подынтегральной функции: |
| + | |||
| + | ::[[Изображение:Q11.png]] | ||
| - | + | Отмtтим, что формулу {{eqref|2}} бывает целесообразно использовать и в обратном порядке, т.е. справа палево. Именно, иногда удобно вычисление интеграла <tex> \int f(x) dx </tex> с помощью | |
Версия 16:33, 16 ноября 2008
Формула замены переменных в неопределенном интеграле
Рассмотрим свойство неопределенного интеграла, часто оказывающееся полезным при вычислении первообразных элементарных функций.
Теорема.
Пусть функции и
определены соответственно на промежутках
и
, причем
. Если функция
имеет на
первообразную
и, следовательно,
(1)
а функция дифференцируема на
, то функция
имеет на
, первообразную
и
(2)
Формула (1) называется формулой интегрирования подстановкой, а именно подстановкой . Это название объясняется тем, что если формулу (2) записать в виде
то будет видно, что, для того чтобы вычислить интеграл 
), можно сделать подстановку и затем вернуться к переменной
естественно сделать подстановку
, тогда
2. Для вычисления интеграла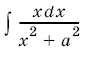 
удобно применить подстановку
:
3. При вычислении интегралов вида 
полезна подстановка
:
Например,
Иногда, прежде чем применить метод интегрирования подстановкой, приходится проделать более сложные преобразования подынтегральной функции:
Отмtтим, что формулу (2) бывает целесообразно использовать и в обратном порядке, т.е. справа палево. Именно, иногда удобно вычисление интеграла с помощью
