Критерий Вальда-Вольфовица

Материал из MachineLearning.

(Различия между версиями)
Перейти к: навигация, поиск
(→Литература)
Строка 17: Строка 17:
# [[Статистический анализ данных (курс лекций, К.В.Воронцов)/2008]]
# [[Статистический анализ данных (курс лекций, К.В.Воронцов)/2008]]
==Литература==
==Литература==
-
* Дерфелль К. Статистика в аналитической химии. — М.: Мир,1994. - 170 с.
+
# Дерфелль К. Статистика в аналитической химии. — М.: Мир,1994. - 170 с.
[[Категория:Энциклопедия анализа данных]]
[[Категория:Энциклопедия анализа данных]]
[[Категория:Регрессионный анализ]]
[[Категория:Регрессионный анализ]]

Версия 11:18, 10 января 2009

Описание критерия

Критерий серий Вальда-Вольфовица может быть использован как тест для анализа регресионных остатков наряду с критерием Уилкоксона-Манна-Уитни, критерием Зигеля-Тьюки, критерием знаков, критерием экстремумов.
В этом случае критерий серий Вальда-Вольфовица испаользуется для проверки гипотезы H0: \varepsilon_{i} - независимая, одинаково распределенная сл. величина, где \varepsilon_{i}=y_{i}-\hat{y_{i}}
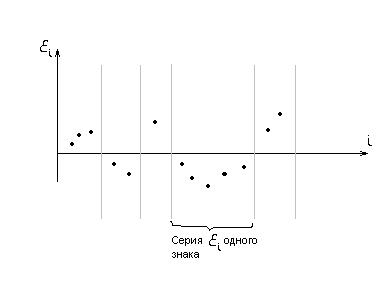
При анализе регресионных остатков будем выделять их в серии одного знака
Изображение:Vald-volf.JPG
Ns - число серий \sim N(ENs,DNs)
E\varepsilon_{i}=0
EN_{s}=\frac{2n_{1}n_{2}}{n_{1}n_{2}}+1, где
n1 - число \varepsilon_{i}\geq0
n2 - число \varepsilon_{i}<0
DN_{s}=\frac{2n_{1}n_{2}}{(n_{1}+n_{2})^{2}}\frac{2n_{1}n_{2}-(n_{1}+n_{2})}{n_{1}+n_{2}-1}
Тогда по критерию серий Вальда-Вольфовица:
\frac{N_{s}-EN_{s}}{\sqrt{DN_{s}}}\sim N(0,1)
Исходя из полученного значения H0 применяется при неком уровне значимости или овтергается.

Смотри также

  1. Статистический анализ данных (курс лекций, К.В.Воронцов)/2008

Литература

  1. Дерфелль К. Статистика в аналитической химии. — М.: Мир,1994. - 170 с.
Источник — «http://machinelearning.ru/wiki/index.php?title=%D0%9A%D1%80%D0%B8%D1%82%D0%B5%D1%80%D0%B8%D0%B9_%D0%92%D0%B0%D0%BB%D1%8C%D0%B4%D0%B0-%D0%92%D0%BE%D0%BB%D1%8C%D1%84%D0%BE%D0%B2%D0%B8%D1%86%D0%B0»
Личные инструменты