Модель Хольта-Уинтерса
Материал из MachineLearning.
(→Определение) |
|||
| Строка 1: | Строка 1: | ||
{{TOCright}} | {{TOCright}} | ||
| - | Многие продукты имеют тенденцию роста или падения продаж, особенно когда они производятся впервые или когда появляются конкурирующие товары. Для некоторых продуктов существенны сезонные изменения уровня продаж | + | Многие продукты имеют тенденцию роста или падения продаж, особенно когда они производятся впервые или когда появляются конкурирующие товары. Для некоторых продуктов существенны сезонные изменения уровня продаж, поэтому для прогноза продаж товара целесообразно учитывать конкретный характер тенденции и сезонных колебаний. На основе [[Модель Хольта|модели Хольта]] Уинтерс (Винтерс, Winters) создал свою прогностическую модель, которая учитывает экспоненциальный [[Тренд|тренда]] и аддитивную [[Сезонность|сезонность]]. |
== Определение == | == Определение == | ||
| Строка 17: | Строка 17: | ||
где s - период [[Сезонность|сезонности]],<tex>\Theta_i, \; i \in 0 \dots s-1</tex> - сезонный профиль, <tex>r_t</tex> - параметр тренда, <tex>а_t</tex> - параметр прогноза, очищенный от влияния тренда и сезонности. | где s - период [[Сезонность|сезонности]],<tex>\Theta_i, \; i \in 0 \dots s-1</tex> - сезонный профиль, <tex>r_t</tex> - параметр тренда, <tex>а_t</tex> - параметр прогноза, очищенный от влияния тренда и сезонности. | ||
| - | Оптимальные параметры <tex>\alpha_1,\; \alpha_2, \; \alpha_3 \in \left( 0,1 \right) </tex> | + | Оптимальные параметры <tex>\alpha_1,\; \alpha_2, \; \alpha_3 \in \left( 0,1 \right) </tex> |
| - | + | предлагается находить экспериментальным путем. Один набор весов можно использовать для широкого класса продуктов, например, Уинтерс использовал данные (за 5—7 лет): о продажах кухонной утвари, о продажах краски, о котлованах для изготовленных заводским способом сооружений и т.п. Первая часть данных (2—3 года) использовалась для построения модели, а на основе остальных данных проверялась точность прогнозирования. | |
| + | |||
| + | == Пример == | ||
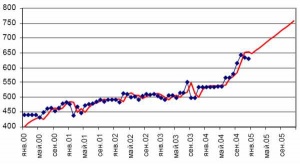
| + | [[Изображение:HoltWintersSample.jpg|300px|thumb|Красным отмечен прогноз, синим - исходные данные.]] | ||
| + | |||
| + | Прогноз арендной ставки на 1 год. Оптимальные параметры <tex>\alpha_1,\; \alpha_2, \; \alpha_3</tex> подбирались путем минимизации среднеквадратичной ошибки прогноза <tex>\eps_t^2=(y_t-\hat{y}_t)^2</tex>. | ||
== Литература== | == Литература== | ||
''Лукашин Ю. П.'' Адаптивные методы краткосрочного прогнозирования временных рядов. — М.: Финансы и статистика, 2003. | ''Лукашин Ю. П.'' Адаптивные методы краткосрочного прогнозирования временных рядов. — М.: Финансы и статистика, 2003. | ||
| + | |||
| + | ''Winters P.R.'' Forecasting sales by exponentially weighted | ||
| + | moving averages //Management Science. - 1960. - Vol. 6. - | ||
| + | №3. | ||
| + | |||
== Ссылки == | == Ссылки == | ||
| Строка 29: | Строка 39: | ||
[[Модель Тейла-Вейджа]] — учитываются аддитивный тренд и сезонность. | [[Модель Тейла-Вейджа]] — учитываются аддитивный тренд и сезонность. | ||
| - | + | ||
| + | [[Скользящий контрольный сигнал| Анализ адекватности адаптивных моделей]] | ||
[[Категория:Прикладная статистика]] | [[Категория:Прикладная статистика]] | ||
[[Категория:Энциклопедия анализа данных]] | [[Категория:Энциклопедия анализа данных]] | ||
Версия 17:33, 11 января 2009
|
Многие продукты имеют тенденцию роста или падения продаж, особенно когда они производятся впервые или когда появляются конкурирующие товары. Для некоторых продуктов существенны сезонные изменения уровня продаж, поэтому для прогноза продаж товара целесообразно учитывать конкретный характер тенденции и сезонных колебаний. На основе модели Хольта Уинтерс (Винтерс, Winters) создал свою прогностическую модель, которая учитывает экспоненциальный тренда и аддитивную сезонность.
Определение
Пусть задан временной ряд: .
Необходимо решить задачу прогнозирования временного ряда.
;
;
;
где s - период сезонности, - сезонный профиль,
- параметр тренда,
- параметр прогноза, очищенный от влияния тренда и сезонности.
Оптимальные параметры
предлагается находить экспериментальным путем. Один набор весов можно использовать для широкого класса продуктов, например, Уинтерс использовал данные (за 5—7 лет): о продажах кухонной утвари, о продажах краски, о котлованах для изготовленных заводским способом сооружений и т.п. Первая часть данных (2—3 года) использовалась для построения модели, а на основе остальных данных проверялась точность прогнозирования.
Пример
Прогноз арендной ставки на 1 год. Оптимальные параметры подбирались путем минимизации среднеквадратичной ошибки прогноза
.
Литература
Лукашин Ю. П. Адаптивные методы краткосрочного прогнозирования временных рядов. — М.: Финансы и статистика, 2003.
Winters P.R. Forecasting sales by exponentially weighted moving averages //Management Science. - 1960. - Vol. 6. - №3.
Ссылки
Модель Брауна — экспоненциальное сглаживание.
Модель Хольта — учитываются линейный тренд без сезонности.
Модель Тейла-Вейджа — учитываются аддитивный тренд и сезонность.