Марковский алгоритм кластеризации
Материал из MachineLearning.
(→Марковский алгоритм кластеризации) |
(→Марковский алгоритм кластеризации) |
||
| Строка 27: | Строка 27: | ||
Моделирование потока в графе осуществляется путем преобразования его в марковский граф (стохастическую матрицу). Рисуйнок 1 | Моделирование потока в графе осуществляется путем преобразования его в марковский граф (стохастическую матрицу). Рисуйнок 1 | ||
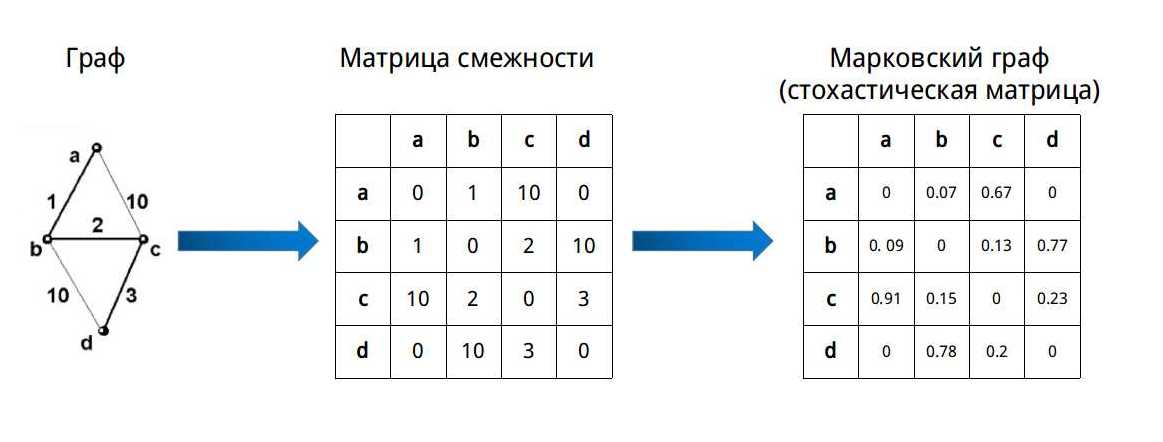
| - | [[Изображение:Graph_to_Markov_Graph.jpg| | + | [[Изображение:Graph_to_Markov_Graph.jpg|50px|frame|Рисуйнок 1. Преобразование графа в марковский граф]] |
На первом шаге граф преобразуется в матрицу растояний между узлами (иное представления графа). На втором шаге происходит преобразование матрицы растояний в матрицу стохастических переходов между узлами. В примере используется нормирование значений в столбце однако может быть применен любой другой алгоритм. | На первом шаге граф преобразуется в матрицу растояний между узлами (иное представления графа). На втором шаге происходит преобразование матрицы растояний в матрицу стохастических переходов между узлами. В примере используется нормирование значений в столбце однако может быть применен любой другой алгоритм. | ||
| Строка 33: | Строка 33: | ||
После того как стохастическая матрица (марковский граф) получена, к ней последовательно применяются применяются две функции (Expansion, распространение) и (Inflation, накачивание) до тех пор пока матррица не перестанет менятся. Рисуйнок 2 | После того как стохастическая матрица (марковский граф) получена, к ней последовательно применяются применяются две функции (Expansion, распространение) и (Inflation, накачивание) до тех пор пока матррица не перестанет менятся. Рисуйнок 2 | ||
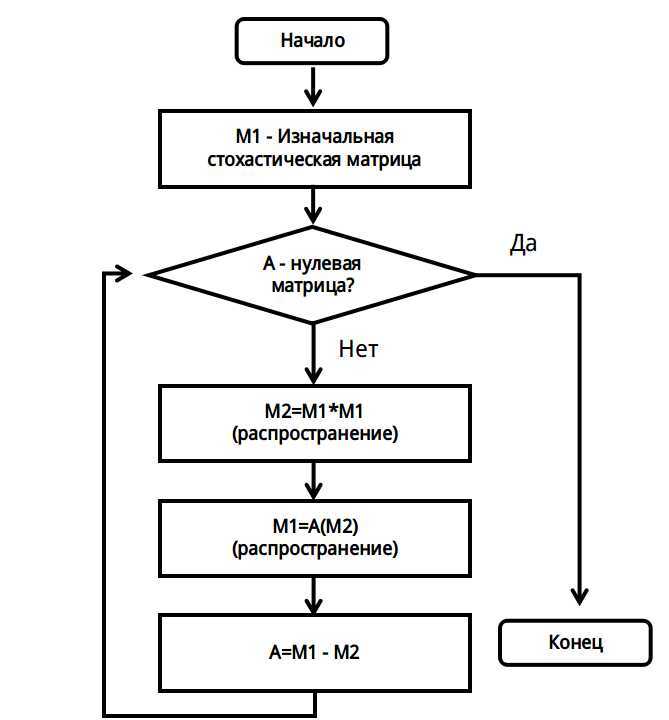
| - | [[Изображение:MCL_algor.jpg| | + | [[Изображение:MCL_algor.jpg|50px|frame|Рисуйнок 2. Блок-схема алгоритма MCL]] |
| Строка 48: | Строка 48: | ||
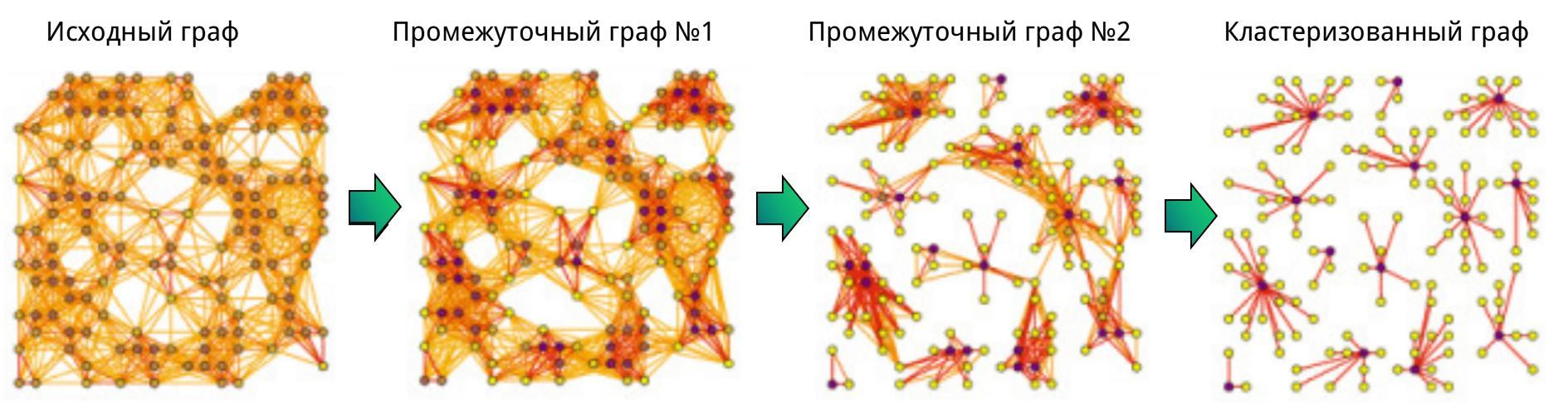
| - | [[Изображение:Markov_Clustering_Algorithm.jpeg| | + | [[Изображение:Markov_Clustering_Algorithm.jpeg|50px|frame| Визуализация метода]] |
Версия 10:19, 2 декабря 2018
| | Данная статья является непроверенным учебным заданием.
До указанного срока статья не должна редактироваться другими участниками проекта MachineLearning.ru. По его окончании любой участник вправе исправить данную статью по своему усмотрению и удалить данное предупреждение, выводимое с помощью шаблона {{Задание}}. См. также методические указания по использованию Ресурса MachineLearning.ru в учебном процессе. |
Марковский алгоритм кластеризации
Марковский алгоритм кластеризации (MCL, Markov Clustering Algorithm) — алкоритм кластерного анализа (таксономия, без учителя), основанный на идеи потока (случайного блуждания) в графе. Изначально разработан для выделения кластеров в графе, однако может быть применен к любым объектам для которых задана матрица сходства/различия.
Данный алгоритм был разработан в рамках PhD работы Van Dongen в 2000 году в центре математических и компьютерных наук в Нидерландах. На сегодняшний день данный алгоритм применяется для данных в молекулярной биологии (выделение групп генов) и анилизе изображений.
В основе алгоритма MCL лежит идея моделирования потока (случайного блуждания) внутри графа.
т.е. если усиливать поток там где он силен и ослаблять его там где он слаб то согласно парадигме кластеризации графа границы между различными кластерами будут исчезать. Таким образом будет выявлена кластерная структура в графе.
общее описание метода
Метод опирается на следующе допущение -
расстояния между узлами графа относящихся к одному кластеру, меншье чем растояние между узлами относящимся к различным кластерам. т.е. поток внутри одного кластера много больше чем между кластерами.
Моделирование потока в графе осуществляется путем преобразования его в марковский граф (стохастическую матрицу). Рисуйнок 1
На первом шаге граф преобразуется в матрицу растояний между узлами (иное представления графа). На втором шаге происходит преобразование матрицы растояний в матрицу стохастических переходов между узлами. В примере используется нормирование значений в столбце однако может быть применен любой другой алгоритм.
После того как стохастическая матрица (марковский граф) получена, к ней последовательно применяются применяются две функции (Expansion, распространение) и (Inflation, накачивание) до тех пор пока матррица не перестанет менятся. Рисуйнок 2
1) expansion - разширяем поток из вершины на потенциальных участников кластера.
2) inflation - уменьшаем переходы между кластерами и увеличиваем внутри кластера.
расширение (expansion) - объединяет кластера, остабляет сильный ток и усиливает слабый.
инфляция (inflation) - сжимает кластера, усиливает сильный поток и ослабляет слабый.
Марковский алгоритм кластеризации — быстрый и масштабируемый алгоритм кластеризации, основанный на моделировании потока в графе.
итог по алгоритму
- Плюсы алгоритма
- Работает как с взвешенными, так и с невзвешенными графами
- Устойчив к шуму в данных
- Количество кластеров не указано заранее, но можно настроить степень детализации кластера с параметрами
- Минусы алгоритма
- Не удается найти перекрывающиеся кластеры (*)
- Не подходит для кластеров большого размера
- Часто кластеры получаются разного размера
В этих двух статьях двугой подход к кластеризации на графе:
L. Hagen and A. B. Kahng, A new approach to effective circuit clustering, in IEEE [91],
pp. 422–427.
C.-W. Yeh, C.-K. Cheng, and T.-T. Y. Lin, Circuit clustering using a stochastic flow injection
method, IEEE Transactions on Computer–Aided Design of Integrated Circuits and Systems,
14 (1995), pp. 154–162.
Список используемой литературы
1) Van Dongen, S. 2000. “Graph clustering by flow simulation.” Ph.D. thesis, University of Utrecht, The Netherlands
2) https://www.micans.org/mcl/index.html
3) Li, Li, Christian J. Stoeckert, and David S. Roos. "OrthoMCL: identification of ortholog groups for eukaryotic genomes." Genome research 13.9 (2003): 2178-2189.
4)Satuluri, Venu, Srinivasan Parthasarathy, and Duygu Ucar. "Markov clustering of protein interaction networks with improved balance and scalability." Proceedings of the first ACM international conference on bioinformatics and computational biology. ACM, 2010.