|
|
| Строка 12: |
Строка 12: |
| | где <tex>K_t</tex> - [[скользящий контрольный сигнал]]. | | где <tex>K_t</tex> - [[скользящий контрольный сигнал]]. |
| | | | |
| - | == Метод половинного деления==
| |
| | | | |
| - | '''Метод половинного деления''' известен также как '''метод бисекции'''. В данном методе интервал делится ровно пополам.
| |
| - |
| |
| - | Такой подход обеспечивает гарантированную сходимость метода независимо от сложности функции - и это весьма важное свойство. Недостатком метода является то же самое - метод никогда не сойдется быстрее, т.е. сходимость метода всегда равна сходимости в наихудшем случае.
| |
| - |
| |
| - | Метод половинного деления:
| |
| - | #Один из простых способов поиска ''корней функции одного аргумента''.
| |
| - | #Применяется для нахождения ''значений действительно-значной функции'', определяемому по какому-либо критерию (это может быть сравнение на ''минимум'', ''максимум'' или конкретное число).
| |
| - |
| |
| - | === Метод половинного деления как метод поиска корней функции ===
| |
| - | ==== Изложение метода ====
| |
| - | Перед применением метода для поиска корней функции необходимо отделить корни одним из известных способов, например, графическим методом. Отделение корней необходимо в случае, если неизвестно на каком отрезке нужно искать корень.
| |
| - |
| |
| - | Будем считать, что корень <tex>t</tex> функции <tex>f(x)=0</tex> отделён на отрезке <tex>[a,b]</tex>. Задача заключается в том, чтобы найти и уточнить этот корень методом половинного деления. Другими словами, требуется найти приближённое значение корня с заданной точностью <tex>\eps</tex>.
| |
| - |
| |
| - | Пусть функция <tex>f</tex> непрерывна на отрезке <tex>[a,b]</tex>,
| |
| - | ::<tex>f(a)\cdot f(b)<0, \; \eps=0,01</tex> и <tex>t\in[a,b]</tex> - единственный корень уравнения <tex>f(x)=0, \; a\le t\le b</tex>.
| |
| - |
| |
| - | (Мы не рассматриваем случай, когда корней на отрезке <tex>[a,b]</tex> несколько, то есть более одного. В качестве <tex>\eps</tex> можно взять и другое достаточно малое положительное число, например, <tex>0,001</tex>.)
| |
| - |
| |
| - | Поделим отрезок <tex>[a,b]</tex> пополам. Получим точку <tex>c= \frac {a+b}{2}, \; a<c<b</tex> и два отрезка <tex>[a,c], \; [c,b]</tex>.
| |
| - | *Если <tex>f(c)=0</tex>, то корень <tex>t</tex> найден (<tex>t=c</tex>).
| |
| - | *Если нет, то из двух полученных отрезков <tex>[a,c]</tex> и <tex>[c,b]</tex> надо выбрать один <tex>[a_1;b_1]</tex> такой, что <tex>f(a_1)\cdot f(b_1)<0</tex>, то есть
| |
| - | **<tex>[a_1;b_1] = [a,c]</tex>, если <tex>f(a)\cdot f(c)<0</tex> или
| |
| - | **<tex>[a_1;b_1] = [c,b]</tex>, если <tex>f(c)\cdot f(b)<0</tex>.
| |
| - | :Новый отрезок <tex>[a_1;b_1]</tex> делим пополам. Получаем середину этого отрезка <tex>c_1=\frac {a_1+b_1}{2}</tex> и так далее.
| |
| - |
| |
| - | Для того, чтобы найти приближённое значение корня с точностью до <tex> \eps >0</tex>, необходимо остановить процесс половинного деления на таком шаге <tex>n</tex>, на котором <tex>|b_n-c_n|<\eps</tex> и вычислить <tex>x=\frac {a_n+b_n}{2}</tex>. Тогда можно взять <tex>t\approx x</tex>.
| |
| - |
| |
| - | ==== Реализация метода на С++ и числовой пример ====
| |
| | | | |
| | | | |
| | | | |
| | {{Задание|Коликова Катя|Vokov|31 декабря 2009}} | | {{Задание|Коликова Катя|Vokov|31 декабря 2009}} |
Модель Тригга-Лича относится к моделям с адаптивными параметрами адаптациями, то есть, является моделью с повышенной способностью к самообучению.
А. Триггом и А. Личем было предложено модифицировать предсказывающие системы, использующие экспоненциальное сглаживание, посредствои изменения скорости реакции в зависимости от величины контнольного сигнала. В простейшей модели это эквивалентно регулированию параметра сглаживания 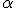 . Наиболее очевидный способ заставить систему автоматически реагировать на расхождение прогнозов и фактических данных - это увеличение
. Наиболее очевидный способ заставить систему автоматически реагировать на расхождение прогнозов и фактических данных - это увеличение 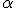 с тем, чтобы придать больший вес свежим данным и, таким образом, обеспечить более быстрое приспособление модели к новой ситуации. Как только система приспособилась, необходимо опять уменьшить величину
с тем, чтобы придать больший вес свежим данным и, таким образом, обеспечить более быстрое приспособление модели к новой ситуации. Как только система приспособилась, необходимо опять уменьшить величину 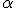 для фильтрации шума.
для фильтрации шума.
. Наиболее очевидный способ заставить систему автоматически реагировать на расхождение прогнозов и фактических данных - это увеличение
с тем, чтобы придать больший вес свежим данным и, таким образом, обеспечить более быстрое приспособление модели к новой ситуации. Как только система приспособилась, необходимо опять уменьшить величину
для фильтрации шума.
,
- скользящий контрольный сигнал.

