Участник:Anton/Песочница

Материал из MachineLearning.

Перейти к: навигация, поиск

Содержание

Основная статья: Графические модели (курс лекций)

Начало выполнения задания: 28 марта 2012

Срок сдачи: 11 апреля 2012, 23:59

Задание состоит из двух вариантов. Распределение вариантов задания по студентам:

Вариант 1 Вариант 2
Ромов Петр, 202 Лямаев Сергей, 202
Иванов Петър, 202 Елшин Денис, 317
Некрасов Константин, 317 Новиков Павел, 317
Меркулова Татьяна, 317 Лобачева Екатерина, 209
Батанов Павел, 321 Птенцов Сергей, 321
Сапатов Александр, 321 Новикова Татьяна, 321
Шальнов Евгений, 321 Конев Артем, 321
Костин Григорий, 320 Икрам Магжан, 325
Переходько Евгения, 325 Парамонов Сергей, 324
Русланова Анна, 421 Ермишин Федор, 321
Исламгулов Ильдар, 420 Грядицкая Юлия, 411
Касперский Иван, 417 Тихонов Андрей, 417
Колев Денис, 417 Вартанов Сергей, 427
Ермаков Михаил, 427 Баранов Леонид, 428
Пироженко Александр, 428 Рябов Сергей, 428
Кузин Сергей, 528 Светличный Дмитрий, ВВО
Заякина Ольга, ВВО Беликов Владимир
Гребенкина Мария Субботин Никита

Среда реализации для всех вариантов — MATLAB. Неэффективная реализация кода может негативно отразиться на оценке.

Марковское случайное поле

Система соседства — прямоугольная решетка
Система соседства — прямоугольная решетка

Марковское случайное поле (MRF) — графическая модель, энергия которой записывается в виде:
E(X) = \sum_{p \in P)} D_p(x_p) + \sum_{(p, q) \in E} V_{pq}(x_p, x_q),
где P — множество индексов переменных, E — система соседства, D — унарные потенциалы, V — бинарные потенциалы.

Рассмотрим модель со следующими ограничениями:

  • переменные x_p дискретны и принимают значения из множества {1,…,K}, K ≥ 2,
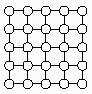
  • система соседства E — прямоугольная решетка,
  • бинарные потенциалы V представимы в виде произведения множителя, не зависящего от значений соседних переменных, и множителя, зависящего только от них:: V_{pq} = c_{pq} d(x_p, x_q) .

В рамках этого задания требуется:

  1. реализовать алгоритм поиска конфигурации X, обладающей минимальной энергией (TRW или α-расширение),
  2. протестировать реализованный алгоритм на модельных задачах,
  3. применить реализованный алгоритм для задачи стерео,
  4. сравнить алгоритмы TRW и α-расширение на задаче стерео.

MRF для стерео

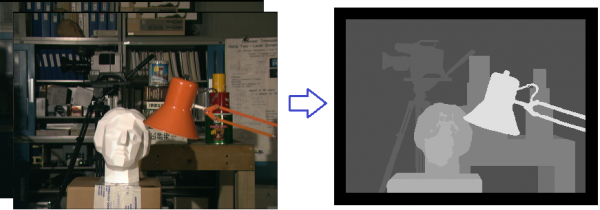
Задача стерео состоит в отнесении каждого пикселя изображения к одному из K классов. В интерактивном варианте пользователь отмечает часть пикселей, принадлежащих каждому классу. После этого требуется автоматически разметить оставшуюся часть изображения.

Для задачи сегментации марковское случайное поле строится следующим образом:

  • Каждая переменная x_p соответствует пикселю изображения.
  • Используется стандартная 4-х связная система соседства.
  • Если пиксель p отнесен пользователем к классу k, то унарные потенциалы „разрешают“ переменной x_p принимать только значение k:
    D_p(k) = 0,\ D_p(l) = +\infty, l \neq k.
  • Если пиксель p не отнесен пользователем ни к одному из классов, то унарные потенциалы принимают значения равные минус логарифму правдоподобия принадлежности пикселя цвета I_p соответствующему классу: D_p(k) = -\log P_k(I_p) .
  • Цветовые модели объектов можно восстановить по пикселям, размеченным пользователем, при помощи EM-алгоритма восстановления смеси нормальных распределений в пространстве YUV.
  • В качестве парных потенциалов выбираются обобщенные потенциалы Поттса, которые поощряют разрезы в тех местах, где цвет изображения сильно меняется: c_{pq} = A + B\:\exp\left(-\frac{|| I_p - I_q ||^2}{2\sigma^2}\right) , A ≥ 0, B ≥ 0, σ — параметры.

Вариант 1 : TRW

Задание

  • Вывести все формулы, использующиеся в вашей реализации TRW (формулировки прямой и двойственной задач, формула подсчета субградиента, конкретная схема субградиентного подъема, и т.д.).
  • Реализовать алгоритм TRW.
  • Протестировать алгоритм TRW на модельных данных (например, решетка 100 x 100, 10 классов, случайные потенциалы).
  • Привести примеры наличия и отсутствия зазора между решениями прямой и двойственной задач (например, зазор должен отсутствовать в случае субмодулярной энергии).
  • Реализовать процедуру сегментации изображений с заданными пользователем семенами.
  • Привести примеры удачных сегментаций (не менее 5). Требуется самостоятельно выбрать изображения (реалистичные), указать семена и отсегментировать при помощи реализованного метода. В отчет нужно вставлять и исходные изображения, и маски семян.
  • На нескольких (не менее 3) задачах сегментации из предыдущего пункта сравнить работу алгоритмов TRW и α-расширение. Реализацию недостающего алгоритма можно взять у товарища, выполняющего другой вариант (в отчете обязательно указывать, чей код вы используете). Требуется провести сравнение по энергии получаемого решения, по времени работы, по визуальному качеству сегментации. Все выводы должны быть подтверждены числами, графиками, картинками.
  • Написать отчет в формате PDF с описанием всех проведенных исследований.

Спецификация реализуемых функций

Алгоритм TRW
[labels, energy, lowerBound, time] = trwGridPotts(unary, vertC, horC)
[labels, energy, lowerBound, time] = trwGridPotts(unary, vertC, horC, options)
ВХОД
unary — унарные потенциалы, массив типа double размера N x M x K, где N — высота решетки, M — ширина решетки, K — количество меток.
vertC — коэффициенты c_{pq}, соответствующие вертикальным ребрам, массив типа double размера (N — 1) x M;
horC — коэффициенты c_{pq}, соответствующие горизонтальным ребрам, массив типа double размера N x (M — 1);
options — (необязательный аргумент) набор дополнительных параметров, массив типа cell вида ParameterName1, ParameterValue1, ParameterName2, ParameterValue2 и т.д. Возможны следующие параметры:
  'maxIter' — максимально допустимое число итераций алгоритма (по умолчанию = 500);
  'argEps' — порог сходимости по аргументу;
  'display' — параметр типа logical: если true, то на каждой итерации нужно выводить на экран номер итерации, текущее значение энергии и нижней границы;
ВЫХОД
labels — разметка, обладающая наименьшей энергией, массив типа double размера N x M;
energy — значения энергии на каждой итерации, вектор типа double длины, равной количеству итераций алгоритма;
lowerBound — значения нижней границы на каждой итерации, вектор типа double длины, равной количеству итераций алгоритма;
time — время, пройденное с начала работы алгоритма до каждой итерации, вектор типа double длины, равной количеству итераций алгоритма.

Обратите внимание: в процедуре trwGridPotts параметры N, M, и K определяются неявно по размеру соответствующих элементов.

Сегментация изображений
[segmentation] = segmentImage(image, seeds)
ВХОД
image — изображение, массив типа double размера N x M x 3 (все значения в этом массиве в интервале от 0 до 1).
seeds — семена, заданные пользователем, массив типа logical размера N x M x K, элементы массива принимают значения true или false;
ВЫХОД
segmentation — сегментация изображения, массив типа double размера N x M со значениями 1,...,K;

Обратите внимание: в процедуре segmentImage параметры N, M, и K определяются неявно по размеру соответствующих элементов.

Рекомендации по выполнению задания

1. При разбиении MRF-решетки только на вертикальные и горизонтальные цепочки формулировка несколько упрощается:

  • Каждое ребро графа принадлежит только одному подграфу, а, значит, не нужно вводить двойственные переменные, соответствующие ребрам.
  • Каждая вершина принадлежит только двум деревьям, а, значит, можно ввести |P|K двойственных переменных, соответствующих условиям y_{pk}^{hor} = y_{pk}^{vert}, \;\; p \in P, \;\; k = 1,\dots,K, где hor и vert обозначают горизонтальную и вертикальную цепочку, проходящую через p-ю вершину.

2. Поскольку двойственная функция вогнута и кусочно-линейна, оптимизировать ее можно при помощи алгоритма субградиентного подъема. Каждый шаг метода субградиентного подъема состоит в пересчете значений двойственных переменных λ по следующему правилу:
\vec{\lambda}_{new} = \vec{\lambda}_{old} + \alpha_t \vec{g}_t, где \vec{g}_t — субградиент в текущей точке, \alpha_t — параметр, отвечающий за длину сдвига. В рамках данного практического задания можно использовать любой способ субградиентного подъема. Например, можно использовать следующий адаптивный метод выбора длины шага:
\alpha_t = \frac{\text{Approx}_t - \text{Dual}_t}{|| \nabla \vec{g}_t|| ^ 2},
где \text{Dual}_t — текущее значение двойственной функции, \text{Approx}_t — оценка оптимума двойственной функции, которую можно определять следующим способом:
\text{Approx}_t = \text{BestDual}_t + \delta_t, где \text{BestDual}_t — лучшее на данный момент значение двойственной функции,
\delta_{t+1} = \begin{cases} \gamma_0 \delta_t, \;\; \text{Dual}_t > \text{Dual}_{t-1}, \\ \max(\gamma_1 \delta_t, \; \varepsilon ), \;\; \text{Dual}_t \leq \text{Dual}_{t-1}. \end{cases}
\gamma_0, \; \gamma_1, \; \varepsilon — параметры метода. Обычно \gamma_0 > 1, \; 1 > \gamma_1 > 0, \; \varepsilon \to 0+ . Конкретные значения этих параметров нужно подобрать.

3. В качестве текущего значения энергии в рамках алгоритма TRW можно выбрать минимум энергий разметок, полученных по только вертикальным и только горизонтальным цепочкам.

4. При тестировании алгоритма TRW необходимо следить, чтобы наибольшее значение нижней границы было не больше, чем наименьшее значение энергии.

5. Для генерации масок семян для сегментации изображений можно использовать любой редактор растровой графики (например, Paint). На изображении нужно определенным цветом закрасить пиксели, относящиеся к маске, и, впоследствии, выделить их в MATLAB.

Данные для выполнения задания

ZIP архив с MATLAB реализацией конвертера изображений.

Оформление задания

Выполненный вариант задания необходимо прислать письмом по адресу bayesml@gmail.com с темой «Задание 2. ФИО, номер группы, вариант 1». Убедительная просьба присылать выполненное задание только один раз с окончательным вариантом. Новые версии будут рассматриваться только в самом крайнем случае. Также убедительная просьба строго придерживаться заданной выше спецификации реализуемых функций. Очень трудно проверять большое количество заданий, если у каждого будет свой формат реализации.

Письмо должно содержать:

  • PDF-файл с описанием проведенных исследований (отчет должен включать в себя описание выполнения каждого пункта задания с приведением соответствующих графиков, изображений, чисел)
  • trwGridPotts.m
  • segmentImage.m
  • Набор вспомогательных файлов при необходимости

Вариант 2 : α-расширение

Задание

  • Вывести все формулы, использующиеся в вашей реализации α-расширения (сведение шага алгоритма к разрезу графа).
  • Реализовать алгоритм α-расширение, используя выданный код разрезов графов.
  • Протестировать алгоритм α-расширение на модельных данных (например, решетка 100 x 100, 10 классов, случайные потенциалы).
  • Реализовать процедуру сегментации изображений с заданными пользователем семенами.
  • Привести примеры удачных сегментаций (не менее 5). Требуется самостоятельно выбрать изображения (реалистичные), указать семена и отсегментировать при помощи реализованного метода. В отчет нужно вставлять и исходные изображения, и маски семян.
  • На нескольких (не менее 3) задачах сегментации из предыдущего пункта сравнить работу алгоритмов TRW и α-расширение. Реализацию недостающего алгоритма можно взять у товарища, выполняющего другой вариант (в отчете обязательно указывать, чей код вы используете). Требуется провести сравнение по энергии получаемого решения, по времени работы, по визуальному качеству сегментации. Все выводы должны быть подтверждены числами, графиками, картинками.
  • Написать отчет в формате PDF с описанием всех проведенных исследований.

Спецификация реализуемых функций

Алгоритм α-расширение
[labels, energy, time] = alphaExpansionGridPotts(unary, vertC, horC)
[labels, energy, time] = alphaExpansionGridPotts(unary, vertC, horC, options)
ВХОД
unary — унарные потенциалы, массив типа double размера N x M x K, где N — высота решетки, M — ширина решетки, K — количество меток.
vertC — коэффициенты c_{pq}, соответствующие вертикальным ребрам, массив типа double размера (N — 1) x M;
horC — коэффициенты c_{pq}, соответствующие горизонтальным ребрам, массив типа double размера N x (M — 1);
options — (необязательный аргумент) набор дополнительных параметров, массив типа cell вида ParameterName1, ParameterValue1, ParameterName2, ParameterValue2 и т.д. Возможны следующие параметры:
  'maxIter' — максимально допустимое число итераций алгоритма (по умолчанию = 500);
  'display' — параметр типа logical: если true, то при каждом запуске алгоритма разреза графа нужно выводить на экран номер итерации, номер расширяемой метки, текущее значение энергии;
ВЫХОД
labels — разметка, обладающая наименьшей энергией, массив типа double размера N x M;
energy — значения энергии на каждой итерации, вектор типа double длины, равной количеству итераций алгоритма;
time — время, пройденное с начала работы алгоритма до каждой итерации, вектор типа double длины, равной количеству итераций алгоритма;

Обратите внимание: в процедуре alphaExpansionGridPotts параметры N, M, и K определяются неявно по размеру соответствующих элементов.

Сегментация изображений
[segmentation] = segmentImage(image, seeds)
ВХОД
image — изображение, массив типа double размера N x M x 3 (все значения в этом массиве лежат в интервале от 0 до 1).
seeds — семена, заданные пользователем, массив типа logical размера N x M x K, элементы массива принимают значения true или false;
ВЫХОД
segmentation — сегментация изображения, массив типа double размера N x M со значениями 1...K;

Обратите внимание: в процедуре segmentImage параметры N, M, и K определяются неявно по размеру соответствующих элементов.

Рекомендации по выполнению задания

  1. Обратите внимание на область применимости алгоритма α-расширение.
  2. При тестировании алгоритма α-расширение необходимо следить за следующим:
    • после каждого применения разреза графа общая энергия не возрастает;
    • значение энергии, выдаваемое функцией graphCutMex, совпадает со значением энергии, подсчитанным независимой процедурой.
  3. Для генерации масок семян для сегментации изображений можно использовать любой редактор растровой графики (например, Paint). На изображении нужно определенным цветом закрасить пиксели, относящиеся к маске, и, впоследствии, выделить их в MATLAB.

Данные для выполнения задания

ZIP архив с MATLAB интерфейсом к разрезам графов.

ZIP архив с MATLAB реализацией конвертера изображений.

Оформление задания

Выполненный вариант задания необходимо прислать письмом по адресу bayesml@gmail.com с темой «Задание 2. ФИО, номер группы, вариант 2». Убедительная просьба присылать выполненное задание только один раз с окончательным вариантом. Новые версии будут рассматриваться только в самом крайнем случае. Также убедительная просьба строго придерживаться заданной выше спецификации реализуемых функций. Очень трудно проверять большое количество заданий, если у каждого будет свой формат реализации.

Письмо должно содержать:

  • PDF-файл с описанием проведенных исследований (отчет должен включать в себя описание выполнения каждого пункта задания с приведением соответствующих графиков, изображений, чисел)
  • alphaExpansionGridPotts.m
  • segmentImage.m
  • Набор вспомогательных файлов при необходимости
Источник — «http://machinelearning.ru/wiki/index.php?title=%D0%A3%D1%87%D0%B0%D1%81%D1%82%D0%BD%D0%B8%D0%BA:Anton/%D0%9F%D0%B5%D1%81%D0%BE%D1%87%D0%BD%D0%B8%D1%86%D0%B0»
Личные инструменты