Интерполяция кубическими сплайнами

Материал из MachineLearning.

Версия от 14:40, 18 октября 2008; Lr2k (Обсуждение | вклад)

(разн.) ← Предыдущая | Текущая версия (разн.) | Следующая → (разн.)

Содержание

1 Введение
- 1.1 Постановка математической задачи
2 Изложение метода
- 2.1 Метод прогонки
3 Численный пример
4 Ошибка интерполяции
- 4.1 Пример: интерполяция синуса
5 Список литературы

Введение

Постановка математической задачи

Одной из основных задач численного анализа является задача об интерполяции функций. Пусть на отрезке $a\le \x\le \b$ задана сетка $\omega=\{x_i:x_0=a<x_1<\cdots<x_i<\cdots<x_n=b\}$ и в её узлах заданы значения функции $y(x)$ , равные $y(x_0)=y_0,\cdots,y(x_i)=y_i,\cdots,y(x_n)=y_n$ . Требуется построить интерполянту — функцию $f(x)$ , совпадающую с функцией $y(x)$ в узлах сетки:

( 1 )

$f(x_i)=y_i, i=0,1,\cdots,n.$

Основная цель интерполяции — получить быстрый (экономичный) алгоритм вычисления значений $f(x)$ для значений $x$ , не содержащихся в таблице данных.

Интерполируюшие функции $f(x)$ , как правило строятся в виде линейных комбинаций некоторых элементарных функций:

$f(x)=\sum_{k=0}^N {c_k\Phi_k(x)},$

где $\{\Phi_k(x)\}$ — фиксированный линейно независимые функции, $c_0, c_1, \cdots, c_n$ — не определенные пока коэффициенты.

Из условия (1) получаем систему из $n+1$ уравнений относительно коэффициентов $\{c_k\}$ :

$\sum_{k=0}^N {c_k\Phi_k(x_i)}=y_i, i=0,1,\cdots,n.$

Предположим, что система функций $\Phi_k(x)$ такова, что при любом выборе узлов $a<x_1<\cdots<x_i<\cdots<x_n=b$ отличен от нуля определитель системы:

$\Delta(\Phi) = \begin{vmatrix} \Phi_0(x_0) & \Phi_1(x_0) & \cdots & \Phi_n(x_0) \\\Phi_0(x_1) & \Phi_1(x_1) & \cdots & \Phi_n(x_1)\\ \cdots & \cdots & \cdots & \cdots \\\Phi_0(x_n) & \Phi_1(x_n) & \cdots & \Phi_n(x_n)\end{vmatrix}$ .

Тогда по заданным $y_i (i=1,\cdots, n)$ однозначно определяются коэффициенты $c_k (k=1,\cdots, n)$ .

Изложение метода

Интерполяция кубическими сплайнами является частным случаем кусочно-полиномиальной интерполцией. В этом специальном случае между любыми двумя соседними узлами функция интерполируется кубическим полиномом. его коэффициенты на каждом интервале определяются из условий сопряжения в узлах:

$f_i=y_i, f'(x_i-0)=f'(x_i+0), f''(x_i-0)=f''(x_i+0), i=1, 2, \cdots, n-1.$

Кроме того, на границе при $x=x_0$ и $x=x_n$ ставятся условия

( 2 )

$f''(x_0)=0, f''(x_n)=0.$

Будем искать кубический полином в виде

( 3 )

$f(x)=a_i+b_i(x-x_{i-1})+c_i(x-x_{i-1})^2+d_i(x-x_{i-1})^3, x_{i-1}\le \x\le \x_i.$

Из условия $f_i=y_i$ имеем

( 4 )

$f(x_{i-1})=a_i=y_{i-1}, f(x_i)=a_i+b_ih_i+c_ih_i^2+d_ih_i^3=y_i, h_i=x_i-x_{i-1}, i=1, 2, \cdots, n-1.$

Вычислим производные:

$f'(x)=b_i+2c_i(x-x_{i-1})+3d_i(x-x_{i-1})^2, f''(x)=2c_i+6d_i(x-x_{i-1}), x_{i-1}\le \x\le \x_i,$

и потребуем их непрерывности при $x=x_i$ :

( 5 )

$b_{i+1}=b_i+2c_ih_i + 3d_ih_i^2, c_{i+1}=c_i+3d_ih_i, i=1, 2, \cdots, n-1.$

Общее число неизвестных коэффициентов, очевидно, равно $4n$ , число уравнений (4) и (5) равно $4n-2$ . Недостающие два уравнения получаем из условия (2) при $x=x_0$ и $x=x_n$ :

$c_1=0, c_n+3d_nh_n=0.$

Выражение из (5) $d_i=\frac{c_{i+1}-c_i}{3h_i}$ , подставляя это выражение в (4) и исключая $a_i=y_{i-1}$ , получим

$b_i=\[\frac{y_i-y_{i-1}}h_i\]-\frac{1}{3}h_i(c_{i+1}+2c_i), i=1, 2, \cdots, n-1, b_n=\[\frac{y_n-y_{n-1}}h_n\]-\frac{2}{3}h_nc_n,.$

Подставив теперь выражения для $b_i, b_{i+1}$ и $d_i$ в первую формулу (5), после несложных преобразований получаем для определения $c_i$ разностное уравнение второго порядка

( 6 )

$h_ic_i+2(h_i+h_{i+1})c_{i+1}+h_{i+1}c_{i+2}=3\left(\frac{y_{i+1}-y_i}{h_{i+1}} - \frac{y_{i+1}-y_i}{h_{i+1}}\right), i=1, 2, \cdots, n-1.$

С краевыми условиями

( 7 )

$c_1=0, c_{n+1}=0.$

Условие $c_{n+1}=0$ эквивалентно условию $c_n+3d_nh_n=0$ и уравнению $c_{i+1} = c_i+d_ih_i$ . Разностное уравнение (6) с условиями (7) можно решить методом прогонки, представив в виде системы линейных алгебраических уравнений вида $~A*x=F$ , где вектор $x$ соответствует вектору $\{c_i\}$ , вектор $F$ поэлементно равен правой части уравнения (6), а матрица $~A$ имеет следующий вид:

$A = \begin{pmatrix} C_1 & B_1 & 0 & 0 & \cdots & 0 & 0 \\ A_2 & C_2 & B_2 & 0 & \cdots & 0 & 0 \\ 0 & A_3 & C_3 & B_3 & \cdots & 0 & 0 \\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & B_{n-1} \\ 0 & 0 & 0 & 0 & \cdots & A_{n} & C_{n} \end{pmatrix},$

где $A_i=h_i, i=2, \cdots, n, B_i = h_{i+1}, i=1, \cdots, n-1$ и $C_i=2(h_i+h_{i+1}), i =1, \cdots, n$ .

Метод прогонки

Метод прогонки, основан на предположении, что искомые неизвестные связаны рекуррентным соотношением:

( 8 )

$x_i = \alpha_{i+1}x_{i+1} + \beta_{i+1}\, i=1,\cdots,n-1$

Используя это соотношение, выразим $x_{i-1}$ и $x_i$ через $x_{i+1}$ и подставим в i-e уравнение:

$\left(A_i\alpha_i\alpha_{i+1} + C_i\alpha_{i+1} + B_i\right)x_{i+1} + A_i\alpha_i\beta_{i+1} + A_i\beta_i + C_i\beta_{i+1} - F_i = 0$

где $F_i$ - правая часть i-го уравнения. Это соотношение будет выполняться независимо от решения, если потребовать

$A_i\alpha_i\alpha_{i+1} + C_i\alpha_{i+1} + B_i = 0$

$A_i\alpha_i\beta_{i+1} + A_i\beta_i + C_i\beta_{i+1} - F_i = 0$

Отсюда следует:

$\alpha_{i+1} = {-B_i \over A_i\alpha_i + C_i}\$

$\beta_{i+1} = {F_i - A_i\beta_i \over A_i\alpha_i + C_i}$

Из первого уравнения получим:

$\alpha_2 = {-B_1 \over C_1}$

$\beta_2 = {F_1 \over C_1}$

После нахождения прогоночных коэффициентов $\alpha$ и $\beta$ , используя уравнение (1), получим решение системы. При этом,

$x_n = {F_n-A_n\beta_n \over C_n+A_n\alpha_n}$

Численный пример

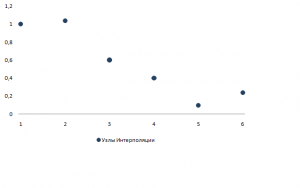
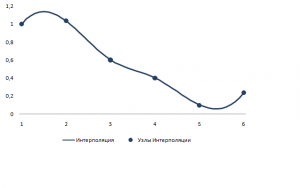
Построим интерполянту для для функции $f$ , заданной следующим образом:

Вводные значения для задачи интерполяции

$x$	$f(x)$
1	1.0002
2	1.0341
3	0.6
4	0.40105
5	0.1
6	0.23975

В результате интерполяции были рассчитаны следующие коэффициенты интерполянты:

Результат интерполяции

$a$	$b$	$c$	$d$	Интервал
1,0002	-0,140113846	0,440979231	-0,266965385	$1\le x\le 2$
1,0341	-0,291901538	-0,359916923	0,217718462	$2\le x\le 3$
0,6	-0,22553	0,293238462	-0,266658462	$3\le x\le 4$
0,40105	-0,100328462	-0,506736923	0,306015385	$4\le x\le 5$
0,1	-0,134456154	0,411309231	-0,137103077	$5\le x\le 6$

Ошибка интерполяции

Нас будет интересовать поведение максимального уклонения сплайна от интерполируемой функции в зависимости от максимального расстояния между соседними узлами интерполирования, т.е. зависимость величины

$\parallel s-f\parallel = \max_{x\in[a,b]}|s(x)-f(x)|$ от шага h, где $h = \max_{k=1,2,\cdots,n-1}|x_{k+1}-x_k|$ . Известно, что если функция $ƒ(x)$ имеет четыре непрерывные производные, то для ошибки интерполяции определенным выше кубическим сплайном s(x) верна следующая оценка <p align = center> $\parallel s-f\parallel \le \frac{5}{384}h^4\parallel \frac{d^4f}{df^4}\parallel причем константа <tex>\frac{5}{384}$ в этом неравенстве является наилучшей из возможных