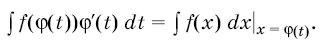Участник:Пасконова Ольга/Песочница

Материал из MachineLearning.

Формула замены переменных в неопределенном интеграле

Рассмотрим свойство неопределенного интеграла, часто оказывающееся полезным при вычислении первообразных элементарных функций.

Теорема.

Пусть функции и определены соответственно на промежутках и , причем . Если функция имеет на первообразную и, следовательно,

(1)

а функция дифференцируема на , то функция имеет на , первообразную и

Формула (1) называется формулой интегрирования подстановкой, а именно подстановкой = х. Это название объясняется тем, что если формулу (2) записать в виде

то будет видно, что, для того чтобы вычислить интеграл ), можно сделать подстановку и затем вернуться к переменной

Иногда, прежде чем применить метод интегрирования подстановкой, приходится проделать более сложные преоб¬разования подынтегральной функции:

Отмстим, что формулу (18,11) бывает целесообразно ис¬пользовать и в обратном порядке, т, с, справа палево. Имен¬но, иногда удобно вычисление интеграла I f(x) dx с помощью" alt= " t , положив х = \phi(t) .

'''Примеры.'''

1, Для вычисления интеграла j cos ax dx ес¬тественно сделать подстановку и = ах, тогда I cos ax dx = - [cos и du = -sin u + C - -sin ax -f С, а ^ 0, Ш 2. Для вычисления интеграла | -= удоопо применить 3 2 подстановку и := х +а :

3. При вычислении интегралов вида J полезна подстановка и = ф(х): I 7-777 Ас = J" ^^ = \ тг = In bfx)l + С. Например,

Иногда, прежде чем применить метод интегрирования подстановкой, приходится проделать более сложные преоб¬разования подынтегральной функции:

Отмстим, что формулу (18,11) бывает целесообразно ис¬пользовать и в обратном порядке, т, с, справа палево. Имен¬но, иногда удобно вычисление интеграла I f(x) dx с помощью" />