Распределение Стьюдента
Материал из MachineLearning.
Плотность вероятности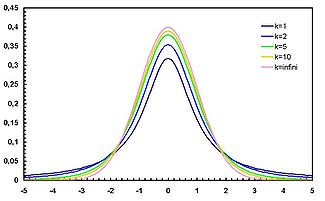
| |
Функция распределения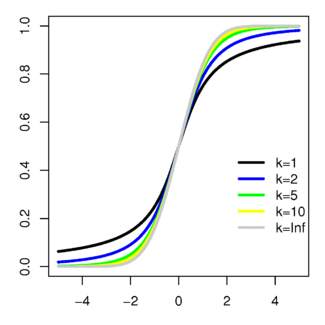
| |
| Параметры | |
| Носитель | |
| Плотность вероятности | |
| Функция распределения | |
| Математическое ожидание | |
| Медиана | |
| Мода | |
| Дисперсия | |
| Коэффициент асимметрии | |
| Коэффициент эксцесса | |
| Информационная энтропия |
|
| Производящая функция моментов | не определена |
| Характеристическая функция | |
Распределе́ние Стью́дента в теории вероятностей — это однопараметрическое семейство абсолютно непрерывных распределений.
Содержание |
Определение
Пусть — независимые стандартные нормальные случайные величины, такие что
. Тогда распределение случайной величины
, где
называется распределением Стьюдента с степенями свободы. Пишут
. Её распределение абсолютно непрерывно и имеет плотность
-
,
где — гамма-функция Эйлера.
Свойства распределения Стьюдента
- Распределение Стьюдента симметрично. В частности если
, то
-
.
Моменты
Случайная величина имеет только моменты порядков
, причём
-
, если
нечётно;
-
, если
чётно.
В частности,
-
,
-
, если
.
Моменты порядков не определены.
Связь с другими распределениями
- Распределение Коши является частным случаем распределения Стьюдента:
-
.
- Распределение Стьюдента сходится к стандартному нормальному при
. Пусть дана последовательность случайных величин
, где
. Тогда
-
по распределению при
.
- Квадрат случайной величины, имеющей распределение Стьюдента, имеет распределение Фишера. Пусть
. Тогда
-
.
- Представление распределения Стьюдента в виде бесконечной смеси Гауссиан:
- Пусть
. Тогда:
-
, где
- плотность нормального распределения,
- плотность гамма распределения
Применение распределения Стьюдента
Распределение Стьюдента используется в статистике для точечного оценивания, построения доверительных интервалов и тестирования гипотез, касающихся неизвестного среднего статистической выборки из нормального распределения. В частности, пусть независимые случайные величины, такие что
. Обозначим
выборочное среднее этой выборки, а
выборочную оценку её дисперсии. Тогда
-
.

