Кривая ошибок

Материал из MachineLearning.

Перейти к: навигация, поиск
Данная статья является непроверенным учебным заданием.
Студент: Участник:osa
Преподаватель: Участник:Константин Воронцов
Срок: 25 января 2010

До указанного срока статья не должна редактироваться другими участниками проекта MachineLearning.ru. По его окончании любой участник вправе исправить данную статью по своему усмотрению и удалить данное предупреждение, выводимое с помощью шаблона {{Задание}}.

См. также методические указания по использованию Ресурса MachineLearning.ru в учебном процессе.


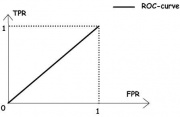
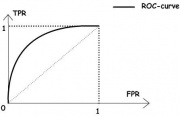
Кривая ошибок или ROC-кривая – часто применяемый способ представления характеристик качества бинарного классификатора.

Содержание

Кривая ошибок в задаче классификации

Рассмотрим задачу логистической регрессии в случае двух классов. Традиционно, один из этих классов будем называть классом «с положительными исходами», другой - «с отрицательными исходами» и обозначим множество классов через Y=\{-1,+1\}. Рассмотрим линейный классификатор для указанной задачи: a(x) = sign (f(x,w) - w_0) .

Параметр w_0 полагается равным \frac{\lambda_{-1}}{\lambda_{+1}}, где \lambda_y – штраф за ошибку на объекте класса y, y \in \{-1, +1\}. Эти параметры выбираются из эмперических соображений и зависят от задачи.

Нетрудно заметить, что в задаче существенны не сами параметры \lambda_y, а их отношение: \frac{\lambda_{-1}}{\lambda_{+1}}. Поэтому при решении задач используются функционалы, инвариантный, относительно этого отношения.

TPR и FPR

Рассмотрим два следующих функционала:

1. False Positive Rate доля объектов выборки X^l ошибочно отнесённых алгоритмом a к классу {+1}:

FPR(a,X^l)=\frac{\sum_{i=1}^l [a(x_i) = +1][y_i = -1]}{\sum_{i=1}^l [y_i = -1]}

2. True Positive Rate доля объектов выборки X^l правильно отнесённых алгоритмом a к классу {+1}:

TPR(a,X^l)=\frac{\sum_{i=1}^l [a(x_i) = +1][y_i = +1]}{\sum_{i=1}^l [y_i = +1]}

ROC-кривая показывает зависимость количества верно классифицированных положительных объектов из X^l (по оси Y) от количества неверно классифицированных отрицательных объектов из X^l (по оси X).

Рис.1. «Случайное гадание»
Рис.1. «Случайное гадание»
На рисунке 1 приведена RoC-кривая, соответствующая алгоритму «случайного гадания», когда классификация объекта происходит методом «подбрасывания монетки» с вероятностью исходов \frac12.
Рис.2. Хороший случай
Рис.2. Хороший случай
На рисунке 2 изображён общий случай. Визуально, чем выше лежит кривая, тем лучше характеристики качества алгоритма.

Алгоритм построения RoC-кривой

На основе обучающей выборки X^l можно очень эффективно аппроксимировать RoC-кривую для заданного классификатора. Ниже приведён алгоритм, строящий эту зависимость.

Вход

  • Обучающая выборка X^l
  • f(x_i,w), \ i=\overline{1,l} — вероятность того, что x_i принадлежит классу {+1}.

Результат работы

\{(FPR_i, TPR_i)\}_{i=0}^l — последовательность из (l+1) точек на координатной плоскости из области [0,1] \times [0,1], аппроксимирующая RoC-кривую по обучающей выборке X^l.

Описание алгоритма

1. Вычислим количество представителей классов {+1} и {-1} в обучающей выборке:
   l_-:= \sum_{i=1}^l [y_i= -1], \ l_+:= \sum_{i=1}^l [y_i= +1] ;
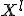2. Упорядочим выборку X^l по убыванию значения f(x_i,w);
3. Начальная точка кривой — (FPR_0,TPR_0):=(0,0);
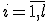4. Цикл для всех  i= \overline{1,l} :
   5.  Если (y_i = -1), то сместиться вправо:
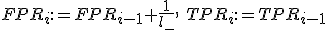        FPR_i:= FPR_{i-1} + \frac{1}{l_-}, \ TPR_i:= TPR_{i-1};
       иначе сместиться вверх:
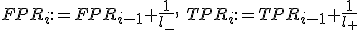        FPR_i:= FPR_{i-1} + \frac{1}{l_-}, \ TPR_i:= TPR_{i-1}+\frac{1}{l_+};


Функционал качества

В качестве функционала качества, инвариантного относительно выбора цен ошибок, используют площадь под RoC-кривой. Эту величину также называют AUC (Area Under Curve). Чем больше AUC, тем «лучше» алгоритм.

Источник — «http://machinelearning.ru/wiki/index.php?title=%D0%9A%D1%80%D0%B8%D0%B2%D0%B0%D1%8F_%D0%BE%D1%88%D0%B8%D0%B1%D0%BE%D0%BA»
Личные инструменты