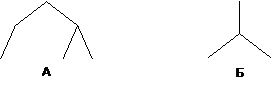Порождение нелинейных регрессионных моделей (пример)
Материал из MachineLearning.
Порождение нелинейных регрессионных моделей - порождение функций, зависящих от параметров и от одной или нескольких свободных переменных. Зависимость от параметров предполагается нелинейной.
Содержание |
Постановка задачи
Задана выборка из пар
. Задан набор порождающих функций одного и двух аргументов
, которые зависят от параметров
и свободных переменных
. Функции гладкие параметрические. Требуется создать алгоритм, порождающий лексикографически упорядоченные суперпозиции возрастающей сложности. Каждая суперпозиция является регрессионной моделью одной независимой переменной. Сравнить качество моделей и регрессионные остатки на порожденном множестве.
Дополнительные предположения
Предполагается, что функции корректно работают в случае вызова в виде
.
Интерпретация на языке деревьев
Заметим вначале, что суперпозиция функций может быть задана двоичным деревом
, вершины которого
∈
, корень – самая внешняя функция суперпозиции. Под глубиной вершины будем понимать расстояние от неё до корня. Если у вершины один потомок, то соответствующая функция запишется как
, если два – то
, если ноль – то
или
.
Так, дереву А соответствует суперпозиция , а дереву Б – суперпозиция
.
Возможна и другая постановка алгоритма. Она особенно ценна, если нельзя вызвать в виде
. Изменение состоит в том, что листья дерева суперпозиции считаются не функциями, а свободными переменными. В этом случае дереву А будет соответствовать суперпозиция
дереву Б – суперпозиция
.
Порождение множества деревьев суперпозиций
Комбинаторная простота этого шага алгоритма заключается в том, что изоморфные деревья задают разные суперпозиции. Однако простые смещения вершин не дают новых деревьев.
Так, деревья А и В различны с точки зрения задаваемых суперпозиций, но деревья А и Б идентичны. Поэтому при машинной реализации можно вообще исключить деревья типа Б, т.е. если из вершины исходит одно ребро, будем «рисовать» его «сверху вниз, справа налево», как в деревьях А и В.
Порождение деревьев осуществим по уровням глубины. Т.е. для задачи порождения деревьев высоты не больше породим все деревья высоты не больше
и запишем их в список
. В список
поместим все деревья высоты ровно
. Далее возьмём дерево из списка
, построим всевозможные деревья высоты
из него, получаемые добавлением рёбер к вершинам нижнего уровня глубины, и поместим их в конец списка
. То же проделаем со всеми остальными деревьями списка
.