Шаговая регрессия (пример)

Материал из MachineLearning.

Перейти к: навигация, поиск

Содержание

Решение практических задач восстановления регрессионной зависимости требует рассмотрения большого числа порождаемых признаков. Процедура построения регрессионных моделей состоит из двух шагов. На первом шаге, на основе свободных переменных- результатов измерений, порождается набор признаков. На втором шаге производится выбор признаков. При выборе признаков выполняется настройка параметров модели, оценивается её качество. Модель с настроенными параметрами, доставляющая минимум заданному функционалу качества, называется моделью оптимальной структуры.

Среди методов отбора признаков широкое распространение получил шаговый метод, впервые предложенный в 1960 году Эфроимсоном. На каждом шаге признаки проверяются на возможность добавления признаков в модель или удаления из модели, основываясь на F-статистике. Также могут быть использованы другие способы определения значимости признака, например, критерий Акаике, Байесовский критерий, критерий Маллоуза.

В данной статье рассматриваются два метода отбора признаков: метод наименьших углов и шаговая регрессия. Эти методы похожи. Различие заключается в том, что алгоритм LARS, вместо последовательного добавления и удаления свободных переменных, на каждом шаге изменяет их веса.

Метод наименьших углов (англ. least angle regression, LARS) - алгоритм отбора признаков в задачах линейной регрессии. При большом количестве свободных переменных возникает проблема неустойчивого оценивания весов модели. LARS предлагает метод выбора такого набора свободных переменных, который имел бы наиболее значимую статистическую связь с зависимой переменной. Также LARS предлагает метод оценки весов.

Шаговая регрессия (stepwise regression)

Цель пошаговой регрессии состоит в отборе из большого количества предикатов небольшой подгруппы переменных, которые вносят наибольший вклад в вариацию зависимой переменной.

Пусть нам задана регрессионная модель

y= f(\beta, x) +\mathbf{\varepsilon},

где x - свободная переменная, y - зависимая переменная, \beta - набор параметров, \varepsilon- случайная аддитивная величина.

Алгоритм заключается в последовательном добавлении и удалении признаков согласно определённому критерию. Обычно используется F -критерий, который имеет вид

F={\frac{S_1-S_2}{S_2}}{\frac{m-p_2}{p_1-p_2}

где индекс 2 соответствует второй регрессионной модели , индекс 1 соответствует первой регрессионной модели, которая является модификацией второй модели; p_1, p_2 - соответствующие числа параметров модели; S- сумма квадратов невязок, задающий критерий качества модели:

S=\sum_{i} {(y^i-f(\beta, x^i))^2

Шаговая регрессия включает два основных шага: шаг Add (последовательное добавление признаков) и шаг Del (последовательное удаление признаков).

Постановка задачи

Задана выборка - матрица X, столбцы которой соответствуют независимым переменным, а строки - элементам выборки и вектор \mathbf{y}, содержащий элементы зависимой переменной. Назначена линейная модель \mathbf{y}=X\mathbf{\beta}+\mathbf{\varepsilon}.

Требуется найти набор признаков (столбцов матрицы X ) , удовлетворяющий F-критерию.

Описание алгоритма

Обозначим текущий набор признаков A . Начальным набором является пустой набор A= \emptyset. К текущему набору A присоединяется по одному признаку, который дoставляет максимум F-критерию или

j^*= arg \max_{j\in J}F_add= arg \max_{j\in J}{\frac{S(A)-S(A\cup x^j)}{S(A\cup x^j)}}

Добавляется несколько признаков, пока значение критерия на шаге не станет меньше заданного F_1 . Затем признаки удаляются по одному так, чтобы значение F-критерия было минимально:

j^*= arg \min_{j\in J}F_del= arg \min_{j\in J}{\frac{S(A/x^j)-S(A)}{S(A)}}

Признаки удаляются , пока значение F-критерия на шаге не станет больше заданного критического значения F_2 .

Критические значения F_1 и F_2 для каждого шага определяются по таблице Фишера c заданным уровнем значимости \alpha со степенями свободы p_1 - p_2 и m - p_2 .

Остановка алгоритма

Останов алгоритма производится при достижении заданного минимума критерием Маллоуза C_p  :

C_p= {\frac{S}{MSE}} +2k - m ,

где MSE= {\frac{S_n}{n}} - среднеквадратичная ошибка, вычисленная для модели, настроенной методом наименьших квадратов на всем множестве признаков, k - сложность модели.

Критерий штрафует модели с большим количеством признаков. Минимизация критерия позволяет найти множество, состоящее из значимых признаков.

Вычислительный эксперимент

Показана работа алгоритмов в серии задач, основанных как на реальных, так и на модельных данных.

Пример 1

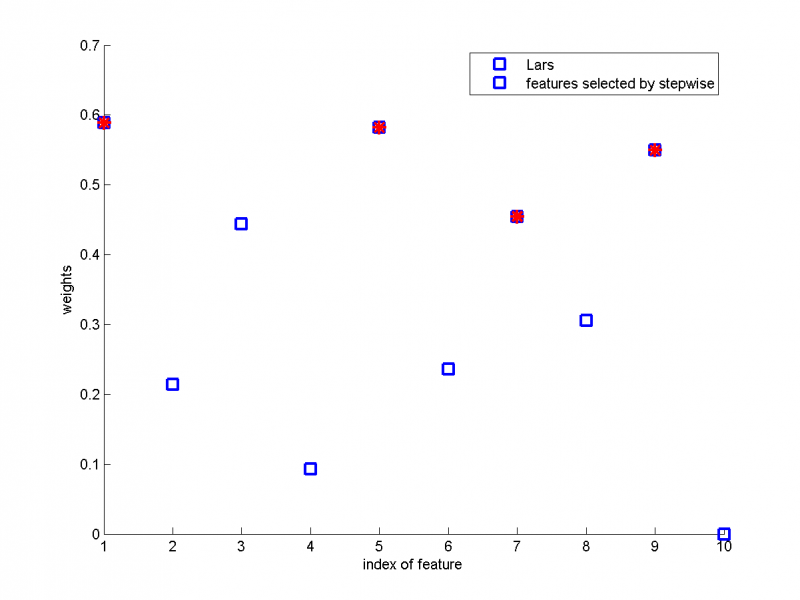
Рассмотрим пример на модельных данных. Сравним два алгоритма: Метод наименьших углов и Шаговую регрессию. Назначена линейная модель, выборка состоит из 20 объектов и 10 признаков. По оси абсцисс показаны номера признаков, по оси ординат- параметры, полученные при использовании Метода наименьших углов. Красным цветом обозначены признаки, выбранные при помощи Шаговой регрессии. Мы видим, что Шаговой регрессией были выбраны 4 признака, которым алгоритмом Lars были присвоены наибольшие значения параметров \beta .

Пример 2

Рассмотрим пример на реальных данных : данные по кредитованию одним из немецких банков . Проведем проверку алгоритма на задаче из репозитория UCI: Statlog (German Credit Data) Data Set. Объектами являются анкеты людей, желавших получить кредит в банке. Изначально анкеты содержали 20 пунктов, таких как состояние банковского счета заемщика, информация о его кредитной истории, цель займа, величина займа, возраст заемщика, время с момента трудоустройства на текущее место работы и другие. Но так как некоторые из них не были числовыми, а многие алгоритмы (в том числе рассматриваемый в данной статье) работают только с числовыми признаками, то из 20 разнородных признаков было составлено 24 числовых. В выборке представлено 256 объектов.

Нахождение модели оптимальной структуры

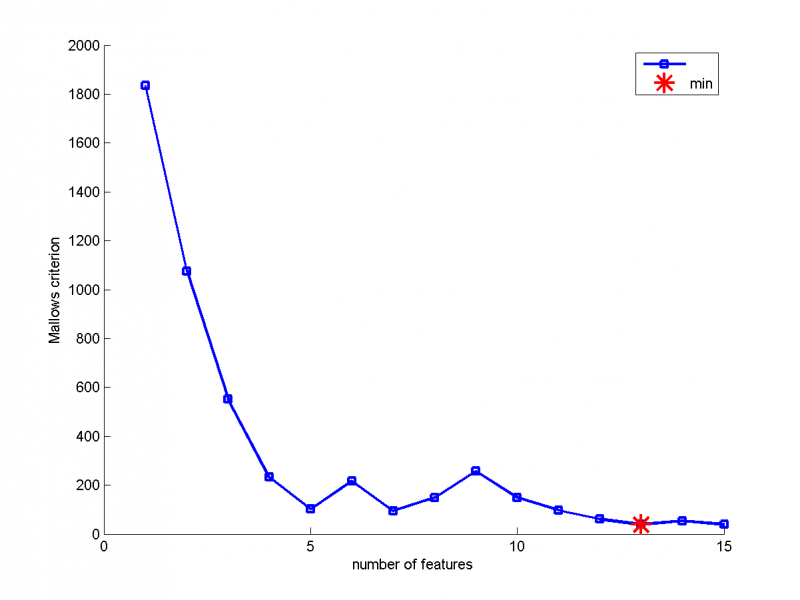
На графике показана зависимость критерия Маллоуза от количества признаков в модели. Из графика мы находим, что минимум критерия Маллоуза достигается при количестве признаков, равном 13. Это и есть модель оптимальной структуры.


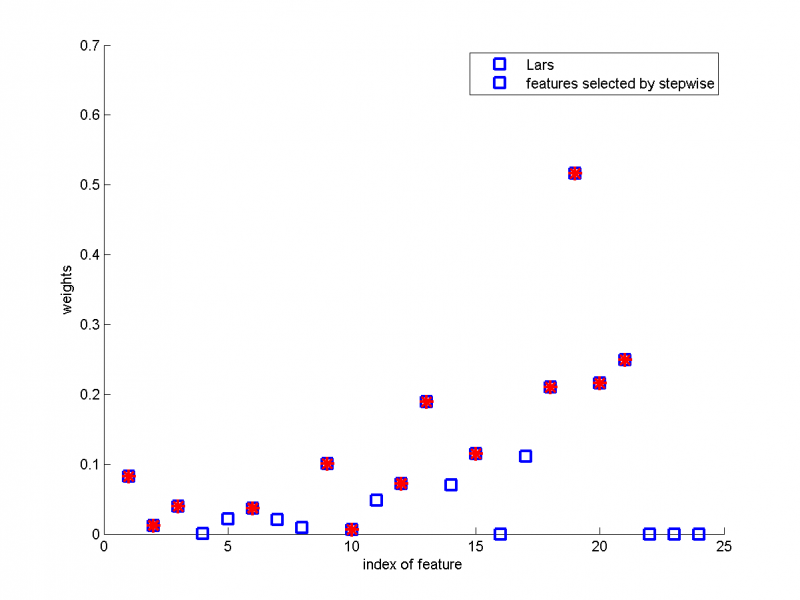
Сравнение работы двух алгоритмов

Аналогично примеру 1, сравним два алгоритма.На графике показана зависимость параметров модели, полученные с помощью Lars, от номера признака. Красным цветом обозначены признаки, выбранные при помощи Шаговой регрессии. В отличие от первого примера на модельных данных, Шаговой регрессией были выбраны несколько признаков, которым Lars присвоил параметры, близкие к нулю. Одним из недостатков метода Шаговой регрессии является то, что важная переменная может быть никогда не включена в модель, а второстепенные признаки будут включены.


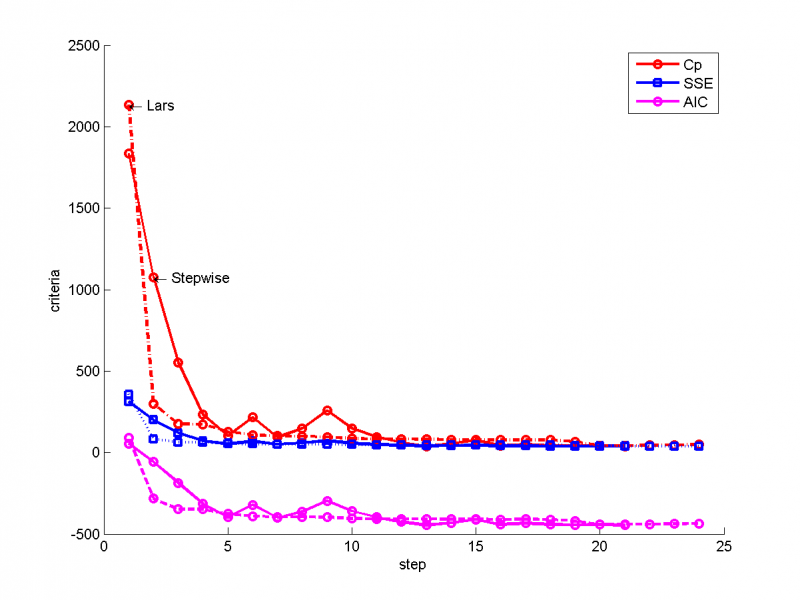
Зависимость критериев от шага алгоритмов

Сравним для двух моделей значения критерия Маллоуза, критерия Акаике и критерия SSE(сумма квадратов регрессионных остатков). Сплошной линией показаны критерии для Шаговой регрессии, пунктирной- для Метода наименьших углов.

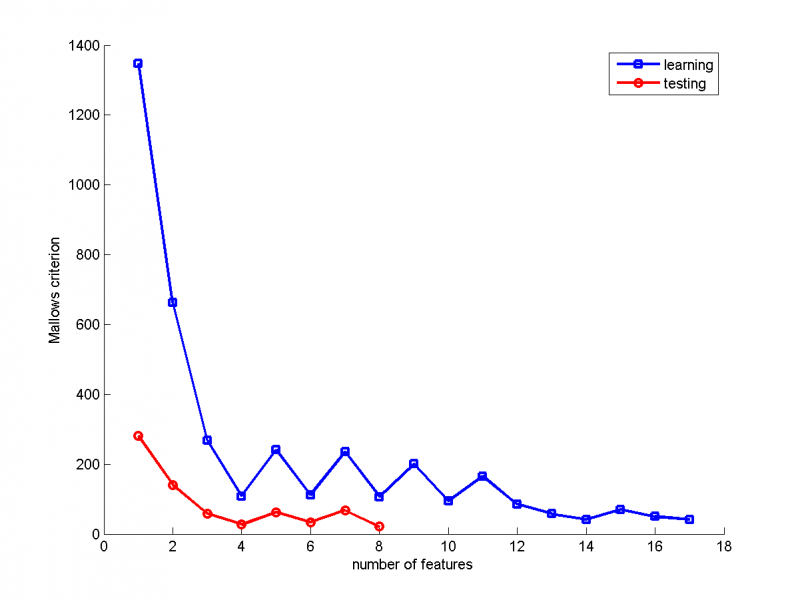
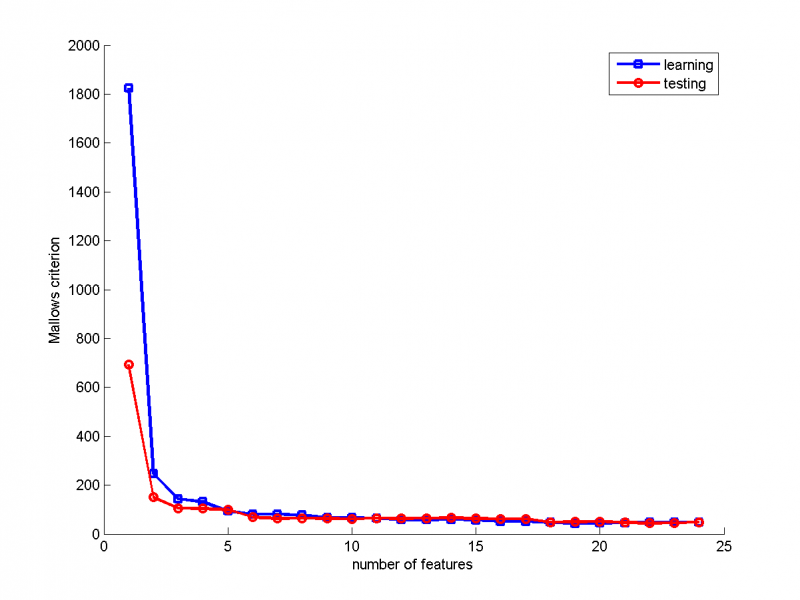
Сравнение критерия Маллоуза для обучающей и тестовой выборки (Stepwise regression)

В качестве обучающей выборки были выбраны 200 объектов, в качестве тестовой- остальные 56.

Сравнение критерия Маллоуза для обучающей и тестовой выборки (Lars)

Исходный код

Скачать листинги алгоритмов можно здесь stepwise.m lars.m Fisher.m

Смотри также

Литература

  • Крымова Е.А., Стрижов В.В. , Алгоритмы выбора признаков линейных регрессионных моделей из конечного и счетного множеств


Данная статья является непроверенным учебным заданием.
Студент: Раиса Джамтырова
Преподаватель: В.В.Стрижов
Срок: 28 мая 2010

До указанного срока статья не должна редактироваться другими участниками проекта MachineLearning.ru. По его окончании любой участник вправе исправить данную статью по своему усмотрению и удалить данное предупреждение, выводимое с помощью шаблона {{Задание}}.

См. также методические указания по использованию Ресурса MachineLearning.ru в учебном процессе.

Источник — «http://machinelearning.ru/wiki/index.php?title=%D0%A8%D0%B0%D0%B3%D0%BE%D0%B2%D0%B0%D1%8F_%D1%80%D0%B5%D0%B3%D1%80%D0%B5%D1%81%D1%81%D0%B8%D1%8F_%28%D0%BF%D1%80%D0%B8%D0%BC%D0%B5%D1%80%29»
Личные инструменты