Непараметрическая регрессия: ядерное сглаживание
Материал из MachineLearning.
| | Статья в настоящий момент дорабатывается. SL 01:27, 12 января 2009 (MSK) |
Ядерное сглаживание - один из простейших видов непараметрической регрессии.
Содержание |
Принцип
Используйщий идейно простой подход к представлению последовательности весов состоит в описании формы весовой функции
посредством функции плотности со скалярным параметром, который регулирует размер и форму весов около х. Эту функцию формы принято называть ядром
.
Последовательность весов
Определение ядра
Ядро — это непрерывная ограниченная симметричная вещественная функция с единичным интегралом
Последовательность весов для ядерных оценок (для одномерного
) определяется как
,
где
,
a
представляет собой ядро с параметром масштаба . Подчеркнув
зависимость
от объема выборки
, условимся сокращен-
но обозначать последовательность весов
.
Функция ядра
Функция является ядерной оценкой плотности Розенблата — Парзена (Rosenblatt, 1956; Parzen, 1962) для (маргинальной) плотности переменной
. Данный вид ядерных весов
был предложен в работах (Nadaraya, 1964) и (Watson, 1964), и, как следствие,
часто называют оценкой Надарая — Ватсона. форма ядерных весов определяется ядром в то время как размер весов параметризируется посредством переменной
, называемой шириной окна. Нормализация весов
позволяет адаптироваться к локальной интенсивности переменной
и, кроме того, гарантирует, что сумма весов равна еденице. Вообще говоря, можно брать различные ядерные функции, нр как практика, так и теория ограничивают выбор. Так, например, ядерные функции, принимающие очень малые значения, могут приводить к машинному нулю компьютера, поэтому разумно рассматривать такие ядерные функции, которые равны нулю вне некоторого фиксированного интервала.
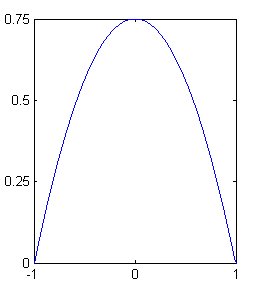
Пример функции ядра
Обычно используется ядерная функция, обладающая некоторыми свойствами оптимальности [Хардле В п4.5]; это функция параболического типа (Epanechnikov, 1969; Bartlett, 1963):
.
Замечание. Ядро не дифференцируемо при . Ядерная оценка не определена для значения ширины окна с
. Если такой случай
возникает, то
определяется как
.
Зависимость от ширины окна
Допустим, что ядерная оценка вычисляется только в точках наблюдений . Тогда при
,
;
следовательно, малая ширина окна воспроизводит данные. Исследуем теперь, что происходит при . Допустим, что
имеет носитель
, как на рис. Тогда
и, следовательно,
Слишком большое значение ширины окна приводит таким образом к чрезмерному сглаживанию кривой — среднему арифметическому значений переменной отклика.
Литература
- Хардле В. Прикладная непараметрическая регрессия. — 1989.