Алгоритм LOWESS

Материал из MachineLearning.

Перейти к: навигация, поиск
Статья плохо доработана.

Имеются указания по её улучшению:


Алгоритм LOWESS (locally weighted scatter plot smoothing) - локально взвешенное сглаживание.

Содержание

Постановка задачи

Решается задача восстановления регрессии. Задано пространство объектов X и множество возможных

ответов Y=R. Существует неизвестная целевая зависимость y^*: X \rightarrow Y, значения которой известны только на объектах обучающей выборки X^m={(x_i, y_i)}_{i=1}^m. Требуется построить алгоритм a: X \rightarrow Y , аппроксимирующий целевую зависимость y^*.

Непараметрическая регрессия

Непараметрическое восстановление регрессии основано на идее, что значение a(x) вычисляется

для каждого объекта x по нескольким ближайшим к нему объектам обучающей выборки.

В формуле Надарая–Ватсона для учета близости объектов x_i обучающей выборки к объекту a(x) предлагалось использовать невозрастающую, гладкую, ограниченную функцию K: [0,\infty) \rightarrow [0,\infty), называемую ядром:

w_i(x) = K\left( \frac{\rho(x, x_i)}{h}\right)

Параметр h называется шириной ядра или шириной окна сглаживания. Чем меньше h, тем быстрее будут убывать веса w_i(x) по мере удаления x_i от x. В общем случае h зависит от объекта x, т.е. h=h(x). Тогда веса вычисляются по формуле \textstyle w_i(x) = K\left( \frac{\rho(x, x_i)}{h(x)}\right)

Оптимизация ширины окна

Чтобы оценить при данном h и K точность локальной аппроксимации в точке x_i, саму эту точку необходимо исключить из обучающей выборки. Если этого не делать, минимум ошибки будет достигаться при h\rightarrow 0. Такой способ оценивания оптимальной ширины окна называется скользящим контролем с исключением объектов по одному (leave-one-out, LOO):

LOO(h,X^m) = \sum_{i=1}^m{\left(a_h(x_i;X^m\setminus\{x_i\}) - y_i \right)^2} \rightarrow min\limits_h

Проблема выбросов

Оценка Надарайя–Ватсона \textstyle a_h(x,X^m) = \frac{\sum_{i=1}^m{y_iw_i}}{\sum_{i=1}^m{w_i}}

крайне чувствительна к большим одиночным выбросам. На практике легко идентифицируются только грубые ошибки, возникающие, например, в результате сбоя оборудования или невнимательности персонала при подготовке данных. В общем случае можно лишь утверждать, что чем больше величина ошибки

\varepsilon_i = \left | a_h \left (x_i;X^m\setminus\{x_i\} \right) -y_i \right |

тем в большей степени прецедент (x_i,y_i) является выбросом , и тем меньше должен быть его вес. Эти соображения приводят к идее домножить веса w_i(x) на коэффициенты \gamma_i = \bar{K}(\varepsilon_i), где \bar{K} — ещё одно ядро, вообще говоря, отличное от K.

Алгоритм LOWESS

Вход

X^m - обучающая выборка;

w_i \, i=1,\ldots,m весовые функции;

Выход

Коэффициенты \gamma_i, i=1,\ldots,m

Алгоритм

1: инициализация
\gamma_i:=1, i=1,\ldots,m
2: повторять
3: вычислить оценки скользящего контроля на каждом объекте:
a_i:=a_h\( x_i;X^m\setminus\{x_i\} \)=\frac{\sum_{j=1,j\ne i}^m y_j\gamma_j w_j}{\sum_{j=1,j\ne i}^m \gamma_j w_j },\;i=1,\ldots,m
4: вычислить новые значения коэффициентов \gamma_i:
\gamma_i:=\bar{K}( \| a_i\;-\;y_i\| ) ,\;i=1,\ldots,m;
5: пока коэффициенты \gamma_i не стабилизируются

Коэффициенты \gamma_i, как и ошибки \varepsilon_i, зависят от функции a_h, которая, в свою очередь, зависит от \gamma_i. На каждой итерации строится функция a_h, затем уточняются весовые множители \gamma_i. Как правило, этот процесс сходится довольно быстро. Он называется локально взвешенным сглаживанием (locally weighted scatter plot smoothing, LOWESS).

Выбор ядра 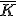\bar{K}

В качестве ядра \bar{K} большинство практических источников рекомендуют

использовать следующее:

Пусть s - есть медиана для оценок \gamma_1,\ldots,\gamma_m, тогда \gamma_i = B(\frac{\varepsilon_i}{6s}), где

B(z)=(1-|z|^2)^2, \, \, |z|<=1 \\ B(z)=0, \,\, |z|>1

Литература

  1. Воронцов К.В. Лекции по алгоритмам восстановления регрессии. — 2007.
  1. A.I. McLeod Statistics 259b Robust Loess: S lowess.

См. также


Данная статья является непроверенным учебным заданием.
Студент: Участник:Валентин Голодов
Преподаватель: Участник:Vokov
Срок: 31 декабря 2009

До указанного срока статья не должна редактироваться другими участниками проекта MachineLearning.ru. По его окончании любой участник вправе исправить данную статью по своему усмотрению и удалить данное предупреждение, выводимое с помощью шаблона {{Задание}}.

См. также методические указания по использованию Ресурса MachineLearning.ru в учебном процессе.


→

Источник — «http://machinelearning.ru/wiki/index.php?title=%D0%90%D0%BB%D0%B3%D0%BE%D1%80%D0%B8%D1%82%D0%BC_LOWESS»
Личные инструменты