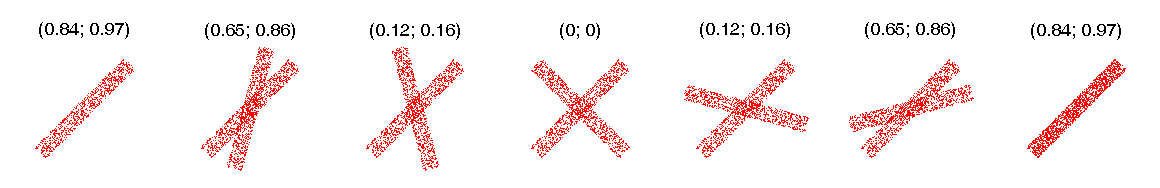Участник:Василий Ломакин/Коэффициент корреляции Кенделла

Материал из MachineLearning.

< Участник:Василий Ломакин

Версия от 12:52, 4 января 2010; Василий Ломакин (Обсуждение | вклад)

(разн.) ← Предыдущая | Текущая версия (разн.) | Следующая → (разн.)

Перейти к: навигация, поиск

Содержание

1 Описание
2 Статистическая проверка наличия корреляции
3 Примеры
4 Связь коэффициентов корреляции Кенделла и Пирсона
5 Связь коэффициентов корреляции Кенделла и Спирмена
6 История
7 Примечания
8 Литература
9 Ссылки

^[1] ^[2]

TODO:

Орфография, пунктуация
Рисунки

Коэффициент корреляции Кенделла — мера линейной связи между случайными величинами. Коэффициент является ранговым, то есть для оценки силы связи используются не численные значения, а соответствующие им ранги. Коэффициент инвариантен по отношению к любому монотонному преобразованию шкалы измерения.

Описание

Заданы две выборки $x = (x_1,\ldots,x_n),\; y = (y_1,\ldots,y_n)$ .

Вычисление корреляции Кенделла

Коэффициент корреляции Кенделла вычисляется по формуле:

$\tau=1-\frac{4}{n(n-1)}R$ , где $R = \sum_{i=1}^{n-1}\sum_{j=i+1}^n\left[ \left[ x_i\ <\ x_j \right] \neq \left[ y_i\ <\ y_j \right] \right]$ — количество инверсий, образованных величинами $y_i$ , расположенными в порядке возрастания соответствующих $x_i$ .

Коэффициент $\tau$ принимает значения из отрезка $[-1;\;1]$ . Равенство $\tau=1$ указывает на строгую прямую линейную зависимость, $\tau=-1$ на обратную.

Обоснование критерия Кенделла

Будем говорить, что пары $(x_i,\; y_i)$ и $(x_j,\; y_j)$ согласованы, если $x_i\ <\ y_j$ и $x_i\ <\ y_j$ или $x_i\ >\ y_j$ и $x_i\ >\ y_j$ , то есть $sign(x_j-x_i)sign(y_j-y_i)=1$ . Пусть $S$ - число согласованных пар, $R$ - число несогласованных пар. Тогда, в предположении, что среди $x_i$ и среди $y_i$ нет совпадений, превышение согласованности над несогласованностью есть:

$T = S - R = \sum_{i < j}sign(x_j-x_i)sign(y_j-y_i)$ .

Для измерения степени согласия Кенделл предложил следующий коэффициент:

$\tau = \frac{T}{max{T}} = \frac{2T}{n(n-1)} = \frac{2(S-R)}{n(n-1)} = 1 - \frac{4}{n(n-1)}R$ .

Таким образом, коэффициент $\tau$ (линейно связанный с $R$ ) можно считать мерой неупорядоченности второй последовательности относительно первой.^[3]

Статистическая проверка наличия корреляции

Нулевая гипотеза $H_0$ : Выборки $x$ и $y$ не коррелируют.

Статистика критерия: $\tau.$

Асимптотический критерий (при уровне значимости $\alpha$ ):

Рассмотрим центрированную и нормированную статистику Кенделла:

$\tilde{\tau} = \frac{\tau}{\sqrt{D_{\tau}}},$ , где $D_{\tau}=\frac{2(2n+5)}{9n(n-1)}$ .

Нулевая гипотеза отвергается (против альтернативы $H_1$ - наличие корреляции), если:

$\left|\tilde{\tau}\right| \ge \Phi_{1-\alpha/2}$ , где $\Phi_{1-\alpha}$ есть $(1-\alpha)$ -квантиль стандартного нормального распределения.

Аппроксимация удовлетворительно работает начиная с $n\geq 10$ .^[4]

Примеры

Ниже приведены примеры вычисления корреляций Кенделла и Спирмена. Значения коэффициентов указаны над каждым изображением в виде $(\tau,\ \rho)$ , где $\tau$ - корреляция Кенделла, $\rho$ - Спирмена. Заметно, что в большинстве случаев \left \rho \right\ >\ \left \tau \right. Объяснение этого эффекта приводится ниже.

Направление линейной зависимости

Нормальные сгущения

Коэффициенты корреляции реагируют на изменение направления и зашумлённость линейной зависимости между переменными.

Наклон линейного тренда

Вращающаяся полоса

Коэффициенты корреляции реагируют на изменение направления, но не реагируют на изменение наклона тренда. На первом, четвёртом и седьмом рисунках дисперсия одной из переменных близка к нулю, поэтому не удаётся зафиксировать факт линейной зависимости.

Нелинейная зависимость

Линейная и нелинейная зависимость

На каждой из приведённых ниже иллюстраций осуществляется переход от линейной зависимости к нелинейной. Коэффициенты корреляции Кенделла и Спирмена реагируют на это одинаковым образом.

Перекрещенные полосы

Расширяющаяся полоса

Синусоида с переменной амплитудой

По мере смены линейной зависимости нелинейной коэффициенты корреляции падают.

Связь коэффициентов корреляции Кенделла и Пирсона

В случае выборок из нормального распределения коэффициент корреляции Кенделла $\tau$ может быть использован для оценки коэффициента корреляции Пирсона $r$ по формуле:

$r=sin{\frac{\pi\tau}{2}}$ .^[5]

Связь коэффициентов корреляции Кенделла и Спирмена

Выборкам $x$ и $y$ соответствуют последовательности рангов:

$R_x=(R_{x_1},\ldots,R_{x_n})$ , где $R_{x_i}$ — ранг $i$ -го объекта в вариационном ряду выборки $x$ ;

$R_y=(R_{y_1},\ldots,R_{y_n})$ , где $R_{y_i}$ — ранг $i$ -го объекта в вариационном ряду выборки $y$ .

Проведем операцию упорядочивания рангов.

Расположим ряд значений $x_i$ в порядке возрастания величины: $x_1\leq x_2\leq\cdots\leq x_n$ . Тогда последовательность рангов упорядоченной выборки $x$ будет представлять собой последовательность натуральных чисел $1,2,\cdots,n$ . Значения $y$ , соответствующие значениям $x$ , образуют в этом случае некоторую последовательность рангов $T=(T_1,\cdots,T_n)$ :

$(R_{x_i},\;R_{y_i})\rightarrow^{sort} (i,\;T_i),\; i=1,\cdots,n$ .

Коэффициент корреляции Кенделла $\tau$ и коэффициент корреляции Спирмена $\rho$ выражаются через ранги $T_i,\; i=1,\cdots,n$ следующим образом:

$\rho=1-\frac{12}{n^3-n}\sum_{i<j}{(j-i)[T_i\ >\ T_j]};$

$\tau=1-\frac{4}{n^2-1}\sum_{i<j}[T_i\ >\ T_j];$

Утверждение.^[6] Если выборки $x$ и $y$ не коррелируют (выполняется гипотеза $H_0$ ), то коэффициент корреляции между величинами $\rho$ и $\tau$ можно вычислить по формуле:

$corr(\rho,\;\tau)=\frac{2n+2}{\sqrt{4n^2+10n}}$ .

История

Критерий был введён в 1938 году известным британским статистиком Морисом Джорджем Кенделлом.

Примечания

↑ Лагутин М. Б. Наглядная математическая статистика. — 223 с.
↑ Кобзарь А. И. Прикладная математическая статистика. — 625 с.
↑ Лагутин М. Б. Наглядная математическая статистика. — 345 с.
↑ Кобзарь А. И. Прикладная математическая статистика. — 625 с.
↑ Кобзарь А. И. Прикладная математическая статистика. — 625 с.
↑ Лагутин М. Б. Наглядная математическая статистика. — 345-346 с.

Литература

Кобзарь А. И. Прикладная математическая статистика. — М.: Физматлит, 2006. — 624-626 с.
Лагутин М. Б. Наглядная математическая статистика. В двух томах. — М.: П-центр, 2003. — 345-346 с.
Лапач С. Н., Чубенко А. В., Бабич П. Н. Статистика в науке и бизнесе. — Киев: Морион, 2002. — 187-189 с.

Ссылки

Ранговая корреляция
Коэффициент корреляции Спирмена — другой способ расчёта ранговой корреляции.
Коэффициент корреляции Пирсона
Коэффициент корреляции — статья в русскоязычной Википедии.
Kendall tau rank correlation coefficient — статья в англоязычной Википедии.

Источник — «http://machinelearning.ru/wiki/index.php?title=%D0%A3%D1%87%D0%B0%D1%81%D1%82%D0%BD%D0%B8%D0%BA:%D0%92%D0%B0%D1%81%D0%B8%D0%BB%D0%B8%D0%B9_%D0%9B%D0%BE%D0%BC%D0%B0%D0%BA%D0%B8%D0%BD/%D0%9A%D0%BE%D1%8D%D1%84%D1%84%D0%B8%D1%86%D0%B8%D0%B5%D0%BD%D1%82_%D0%BA%D0%BE%D1%80%D1%80%D0%B5%D0%BB%D1%8F%D1%86%D0%B8%D0%B8_%D0%9A%D0%B5%D0%BD%D0%B4%D0%B5%D0%BB%D0%BB%D0%B0»