Классификация пациентов с сердечно-сосудистыми заболеваниями (отчет)

Материал из MachineLearning.

Версия от 15:52, 22 февраля 2010; Maxx (Обсуждение | вклад)

(разн.) ← Предыдущая | Текущая версия (разн.) | Следующая → (разн.)

Перейти к: навигация, поиск

Введение в проект

Описание проекта

Цель проекта

Цель проекта - классификация пациентов с подозрением на сердечно-сосудистые заболевания по группам риска.

Обоснование проекта

Полученные результаты могут быть использованы для предварительной диагностики заболевания у пациентов.

Описание данных

Дан список 100 пациентов с указанием их группы риска(по экспертной оценке) и результатов их анализов по 20 параметрам.

Критерии качества

Критерием качества является общее количество ошибок классификации. При этом не допускается более 1 ошибки для пациентов групп риска A1(уже прооперированные больные) и A3(больные с высокой вероятностью заболевания).

Требования к проекту

Алгоритм не должен допускать более одной ошибки по группам риска A1 и A3, а также минимальное количество ошибок по остальным группам риска.

Выполнимость проекта

Особенностями данных, которые могут затруднить выполнение проекта, являются малое количество прецедентов по некоторым группам риска(в особенности A2) и наличие пропусков в данных.

Используемые методы

Предполагается использовать линейные алгоритмы классификации, в частности SVM.

Постановка задачи

Дана обучающая выборка $X^\ell = (x_i, y_i)_{i=1}^\ell, ~~ \ell = 66$ , где $x_i \in \mathbb{R}^n, n = 20$ , $y_i \in \{A_1, A_3, B_1, B_2\}$ .

Для каждой из задач двуклассовой классификации(отделение одного класса от трех остальных и отделение пар классов друг от друга) перекодируем классы так, что $y_i \in \{-1, 1\}$ . Требуется подобрать вектор параметров $\mathbf{w}$ оптимальной разделяющей гиперплоскости, который минимизирует функционал скользящего контроля: $LOO(\mathbf{w},X^\ell) = \sum_{i=1}^\ell [a(x_i, X^\ell\backslash x_i, \mathbf{w}) \neq y_i] \rightarrow \min_{\mathbf{w}}$ , где $a(x) = [\sum_{j=1}^n w_jx^j-w_0 > 0]$

Описание алгоритмов

Базовые предположения

Особенностью данной задачи является большая размерность признакового пространства и малое число прецедентов. Таким образом для того, чтобы избегнуть переобучения и добиться устойчивой классификации, требуется решить задачу отбора признаков. Для этой цели предполагается использовать алгоритм Relevance Kernel Machine with supervised selectivity(далее - $\mu - RKM$ ), который совмещает в себе возможности решения задачи классификации и отбора признаков.

Математическое описание алгоритмов

Квази-вероятностная постановка задачи

Пусть $\Omega$ - множество объектов, каждый из которых принадлежит одному из двух классов: $y(\omega) \in Y = \{-1, 1\}$ . Каждый объект $\omega \in \Omega$ характеризуется $n$ признаками в некоторых шкалах $x^i(\omega) \in X_i$ . Пусть в пространстве признаков $X = X_1 \times \dots \times X_n$ объективно определена некоторая неизвестная гиперплоскость $\sum_{i=1}^n K_i(\vartheta_i, x^i) + b = 0$ . В качестве модели распределения объектов рассмотрим два несобственных параметрических распределения:

$\varphi_{+1}(x^1, \dots, x^n | \vartheta_1, \dots, \vartheta_n, b) = \left\{ \begin{array}{l} 1, ~ \sum_{i=1}^n K_i(\vartheta_i, x^i) + b \ge 1, \\ \exp{\bigl[-c\bigl(1 - \sum_{i=1}^n K_i(\vartheta_i, x^i) - b \bigr)\bigr]}, ~ \sum_{i=1}^n K_i(\vartheta_i, x^i) + b < 1, \\ \end{array} \right.$ $\varphi_{-1}(x^1, \dots, x^n | \vartheta_1, \dots, \vartheta_n, b) = \left\{ \begin{array}{l} 1, ~ \sum_{i=1}^n K_i(\vartheta_i, x^i) + b \le -1, \\ \exp{\bigl[-c\bigl(1 + \sum_{i=1}^n K_i(\vartheta_i, x^i) + b \bigr)\bigr]}, ~ \sum_{i=1}^n K_i(\vartheta_i, x^i) + b > -1. \\ \end{array} \right.$

Далее вектор $(\vartheta_1, \dots, \vartheta_n, b)$ рассмотрим как случайный вектор с априорной плотностью распределения $\Psi(\vartheta_1, \dots, \vartheta_n, b).$ По формуле Байеса апостериорная плотность распределения параметров $\mathbf{\vartheta}$ и $b$ : $P\bigl(\mathbf{\vartheta}, b| X^{\ell}\bigr)\prop \Psi(\mathbf{\vartheta}, b) \biggl(\prod_{j: y_j = +1} \varphi_{+1}(\mathbf{x_j} | \mathbf{\vartheta}, b)\biggr)\biggl(\prod_{j: y_j = -1} \varphi_{-1}(\mathbf{x_j} | </p> \mathbf{\vartheta}, b)\biggr)$

Согласно принципу максимизации апостериорной плотности распределения:

$\bigl(\hat{\vartheta_1}, \dots, \hat{\vartheta_n}, \hat{b}\bigr) = arg \max_{\mathbf{\vartheta}, b} \biggl[\ln \Psi(\mathbf{\vartheta}, b) + \sum_{j: y_j = +1} \ln \varphi_{+1}(\mathbf{x_j} | \mathbf{\vartheta}, b) + \sum_{j: y_j = -1} \ln \varphi_{-1}(\mathbf{x_j} | \mathbf{\vartheta}, </p> b)\biggr]$

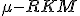
Метод $\mu - RKM$

Пусть априорные плотности распределения компонент $\vartheta_i$ направляющего вектора разделяющей гиперплоскости имеют нормальные распределения с нулевыми математическими ожиданиями и дисперсиями $r_i$ : $\psi(\vartheta_i|r_i) = \frac{1}{\sqrt{2\pi r_i}}\exp\bigl(-\frac{1}{2r_i}K_i(\vartheta_i, \vartheta_i)\bigr)$

Будем считать, что параметр $b$ имеет равномерное несобственное распределение, равное единице на всей числовой оси. Тогда плотность распределения вектора $\mathbf{\vartheta}$ пропорциональна:

$\Psi(\vartheta_1, \dots, \vartheta_n|r_1, \dots, r_n) \prop \bigl(\prod_{i=1}^n r_i\bigr)^{-1/2}\exp\bigl(-\sum_{i=1}^n\frac{1}{2r_i}K_i(\vartheta_i, \vartheta_i)\bigr)$

Положим, что все величины $\frac{1}{r_i}$ имеют априорное гамма распределение:

$\gamma(\frac{1}{r_i}|\alpha,\beta) \prop (1/r_i)^{\alpha - 1} \exp(-\beta(1/r_i))$ .

Примем что $\alpha = \frac{(1 + \mu)^2}{2\mu}, \beta = \frac{1}{2\mu}$ , где $\mu$ - некоторый неотрицательный параметр.

Принцип максимизации совместной апостериорной плотности приводит к критерию обучения:

$\left\{\sum_{i=1}^n \bigl[\frac{1}{r_i}\bigl(K_i(\vartheta_i, \vartheta_i) + \frac{1}{\mu}\bigr) + \bigl( \frac{1}{\mu} + 1 + \mu \bigr)\bigr] + C\sum_{j=1}^{\ell} \delta_j \to \min(\mathbf{\vartheta}, \mathbf{r}, b, \mathbf{\delta}), \\ y_j\biggl(\sum_{i=1}^n K_i\bigl(\vartheta_i, x_i(\omega_j)\bigr)\biggr) \ge 1 - \delta_j, ~ \delta_j \ge 0, j = 1, \dots, \ell. </p> \right.$

Для каждой итерации при фиксированном приближении( $r_i^k, i = 1, \dots, n$ ) решение данной оптимизационной задачи сводится лишь к небольшой модификации классического SVM.

Если же найдено текущее приближение $(\vartheta_1^k, \dots, \vartheta_n^k, b^k)$ , то следующее приближение $r_1^{k+1}, \dots, r_n^{k+1}$ может быть найдено из простого соотношения: $r_i^{k+1} = \frac{K_i(\vartheta_i, \vartheta_i) + \frac{1}{\mu}}{\frac{1}{\mu} + 1 + \mu}$

Отбор признаков

Для повышения устойчивости алгоритма был применен дополнительный отбор признаков. Для этого производился предварительный запуск алгоритма RKM и рассматривался полученный вектор весов признаков: $\hat{r}_i, i = 1, \dots, n$ . Далее из набора признаков удалялись те из них , для которых $\frac{\max_j ~ \hat{r}_j}{\hat{r}_i} > \gamma, i = 1, \dots, n$ , где $\gamma$ - дополнительный параметр селективности. На модифицированном наборе признаков алгоритм RKM запускался еще раз для получения окончательной классификации.

Варианты или модификации

Параметрами алгоритма являются $C \in [0, \infty], ~ \mu \in [0, \infty], ~ \gamma \in [1, \infty]$ , наилучшие значения которых требуется выбрать в результате эксперимента.

Описание системы

Описание системы находится в файле Systemdocs1.docx Файлы системы можно скачать здесь: SelRKM.m, GetRelevantFeatures.m, GetStatsIfClassification.m

Отчет о вычислительных экспериментах

% OneVsOthersTest - script which tests RKM algorithm cardiovascular diseases train set 
%                   in problems of classification one class vs 3 other classes
% Author: Maxim Panov, MIPT, group 674
%
% Input: excel-files with objects-features matrices of 4 types of patients 
%
% Output: 
%   statistics - 4 x 3 x 4 structure: 
%   statistics(k, j, i) - statistics of classification(with fields like 
%                         in output of GetStatsOfClassification) of class i
%                         with selectivityLevel 0.1*10^k and C = 100*10^j
 
%% Upload data
UploadData;
trainSet = allData;
types = [repmat(1, size(a1, 1), 1); 
        repmat(2, size(a3, 1), 1);
        repmat(3, size(b1, 1), 1);
        repmat(4, size(b2, 1), 1)]; 
 
%% Set selectivity rate    
selectivityRate = 10; 
 
%% Compute statistics of classification
for i = 1 : 4
    supplTrainSet = [trainSet(types == i, :); trainSet(types ~= i, :)];
    supplTypes =  [repmat(1, size(types(types == i, :), 1), 1); repmat(-1, size(types(types ~= i, :), 1), 1)];
    C = 100;    
    for j = 1 : 3 
        C = C * 10;
        selectivity = 0.1;
        for k  = 1 : 4
            selectivity = selectivity * 10;
            supplStatisticsA(k, 1) = GetStatsOfClassification(supplTrainSet, supplTypes, C, selectivity, selectivityRate);
        end
        if j == 1
            supplStatisticsB = supplStatisticsA;
        else
            supplStatisticsB = cat(2, supplStatisticsB, supplStatisticsA); 
        end  
    end
    if i == 1
        statistics = supplStatisticsB;
    else
        statistics = cat(3, statistics, supplStatisticsB); 
    end  
 
end

Анализ качества работы алгоритма

На основании полученных результатов для каждой из четырех подзадач классификации можно выбрать наилучшие значения параметров, статистика классификации для которых приведена в таблице:

Class	C	SelectivityLevel	SelectivityRate	Test error	LOO
A1	10000	1000	30	5	15
A3	10000	1000	30	0	5
B1	10000	1000	10	23	23
B2	100000	100	30	11	20

Список литературы

Данная статья является непроверенным учебным заданием.

Студент: Максим Панов

Преподаватель: В. В. Стрижов

Срок: 15 декабря 2009

До указанного срока статья не должна редактироваться другими участниками проекта MachineLearning.ru. По его окончании любой участник вправе исправить данную статью по своему усмотрению и удалить данное предупреждение, выводимое с помощью шаблона {{Задание}}.

См. также методические указания по использованию Ресурса MachineLearning.ru в учебном процессе.

Источник — «http://machinelearning.ru/wiki/index.php?title=%D0%9A%D0%BB%D0%B0%D1%81%D1%81%D0%B8%D1%84%D0%B8%D0%BA%D0%B0%D1%86%D0%B8%D1%8F_%D0%BF%D0%B0%D1%86%D0%B8%D0%B5%D0%BD%D1%82%D0%BE%D0%B2_%D1%81_%D1%81%D0%B5%D1%80%D0%B4%D0%B5%D1%87%D0%BD%D0%BE-%D1%81%D0%BE%D1%81%D1%83%D0%B4%D0%B8%D1%81%D1%82%D1%8B%D0%BC%D0%B8_%D0%B7%D0%B0%D0%B1%D0%BE%D0%BB%D0%B5%D0%B2%D0%B0%D0%BD%D0%B8%D1%8F%D0%BC%D0%B8_%28%D0%BE%D1%82%D1%87%D0%B5%D1%82%29»

Категория: Непроверенные учебные задания