Метод градиентного спуска

Материал из MachineLearning.

Версия от 18:28, 17 мая 2010; Yury Chekhovich (Обсуждение | вклад)

(разн.) ← Предыдущая | Текущая версия (разн.) | Следующая → (разн.)

Перейти к: навигация, поиск

Содержание

1 Введение
2 Метод градиентного спуска
3 Числовые примеры
4 Рекомендации программисту
5 Заключение
6 Ссылки
7 Список литературы

Введение

В работе рассматривается задача поиска минимума функции $f(x): \mathbb{R}^n \to \mathbb{R}$ , записываемая в виде:

(1)

$f(x) \to \min_{x \in \mathbb{R}^n}$

Пусть функция $f(x)$ такова, что можно вычислить ее градиент. Тогда можно применить метод градиентного спуска, описанный в данной статье.

В статье приведены теоремы сходимости метода градиентного спуска, а также рассмотрена его варианты:

Метод градиентного спуска с постоянным шагом
Метод градиентного спуска с дроблением шага
Метод наискорейшего спуска

Метод градиентного спуска

Рис.1 Геометрическая интерпретация метода градиентного спуска с постоянным шагом. На каждом шаге мы сдвигаемся по вектору антиградиента, "уменьшенному в $\lambda$ раз".

Идея метода

Основная идея метода заключается в том, чтобы осуществлять оптимизацию в направлении наискорейшего спуска, а это направление задаётся антиградиентом $-\nabla f$ :

$x^{[k+1]}=x^{[k]}-\lambda^{[k]}\nabla f(x^{[k]})$

где $\lambda^{[k]}$ выбирается

постоянной, в этом случае метод может расходиться;
дробным шагом, т.е. длина шага в процессе спуска делится на некое число;
наискорейшим спуском: $\lambda^{[k]}=\arg\min_{\lambda} \,f(x^{[k]}-\lambda\nabla f(x^{[k]}))$

Алгоритм

Вход: функция $f: \mathbb{R}^n \to \mathbb{R}$

Выход: найденная точка оптимума $x$

Повторять:
$x^{[k+1]}=x^{[k]}-\lambda^{[k]}\nabla f(x^{[k]})$ , где $\lambda^{[k]}$ выбирается одним из описанных выше способов
если выполен критерий останова, то возвращаем текущее значение $x^{[k+1]}$

Критерий останова

Критерии остановки процесса приближенного нахождения минимума могут быть основаны на различных соображениях. Некоторые из них:

$||x^{[k+1]}-x^{[k]}||\leq\eps$
$||f(x^{[k+1]})-f(x^{[k]})||\leq\eps$

Здеcь $x^{[k]} \in \mathbb{R}^n$ - значение, полученное после $k$ -го шага оптимизации. $\eps$ - наперед заданное положительное число.

Сходимость градиентного спуска с постоянным шагом

Теорема 1 о сходимости метода градиентного спуска спуска с постоянным шагом.

Пусть $\lambda^{[k]}=\lambda=const$ , функция $f$ дифференцируема, ограничена снизу. Пусть выполняется условие Липшица для градиента $f'(x)$ : $||f'(x)-f'(y)|| \leq L ||x-y||$ . Пусть $0<\lambda<2/L$ .

Тогда $\lim_{k \to \infty}f'(x^{[k]}) = 0, \; f(x^{[k+1]})<f(x^{[k]})$ при любом выборе начального приближения.

В условиях теоремы градиентный метод обеспечивает сходимость $\{ x^{[k]} \}$ либо к точной нижней грани $\inf_x f(x)$ (если функция $f(x)$ не имеет минимума) либо к значению $f(x*): \;\lim_{k \to \infty}x^{[k]} = x*,\; f'(x*)=0.$ Существуют примеры, когда в точке $x*$ реализуется седло, а не минимум. Тем не менее, на практике методы градиентного спуска обычно обходят седловые точки и находят локальные минимумы целевой функции.

Определение. Дифференцируемая функция $f$ называется сильно выпуклой (с константой $\Lambda>0$ ), если для любых $x$ и $y$ из $\mathbb{R}^n$ справедливо

$f(x+y)\geq f(x)+ \langle f'(x) ,y \rangle + \Lambda||y||^2/2 .$

Теорема 2 о сходимости метода градиентного спуска спуска с постоянным шагом.

Пусть функция $f$ дифференцируема, сильно выпукла с константой $\Lambda$ . Пусть выполняется условие Липшица для градиента $f'(x)$ : $||f'(x)-f'(y)|| \leq L ||x-y||$ . Пусть $0<\lambda<2/L$ .

Тогда $\lim_{k \to \infty}x^{[k]} = x*, \; ||x^{[k]}-x*||\leq q^k ||x^{[0]}-x*||, \; q = \max\{|1-\lambda\Lambda|, |1-\lambda L |\}$ при любом выборе начального приближения.

Выбор оптимального шага

Рис.2 Ситуация, когда метод гардиентного спуска сходится плохо.

Константа $q$ , фигурирующая в теореме 2 и характеризующая скорость сходимости метода, зависит от шага $\lambda$ . Нетрудно видеть, что величина $q=q(\lambda)=\max\{|1-\lambda\Lambda|, |1-\lambda L |\}$ минимальна, если шаг $\lambda$ выбирается из условия $|1-\lambda\Lambda| = |1-\lambda L |$ , т. е. если $\lambda = \lambda* = 2/(\Lambda + L)$ .

При таком выборе шага оценка сходимости будет наилучшей и будет характеризоваться величиной:

$q=q*=\frac{L-\Lambda}{L+\Lambda}$ .

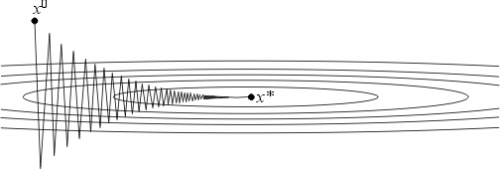
В качестве $\Lambda$ и $L$ могут выступать равномерные по x оценки сверху и снизу собственных значений оператора $f''(x)$ . Если $\lambda << \Lambda$ , то $q*\approx 1$ и метод сходится очень медленно. Геометрически случай $\lambda << \Lambda$ соответствует функциям с сильно вытянутыми линиями уровня (см. рис. 2). Простейшим примером такой функции может служить функция на $\mathbb{R}^2$ , задаваемая формулой:

$f(x_1,x_2)=\Lambda x_1^2 + L x_2^2, \; \Lambda << L$ .

Поведение итераций градиентного метода для этой функции изображено на рис. 2 — они, быстро спустившись на "дно оврага", затем медленно "зигзагообразно" приближаются к точке минимума. Число $\mu = L/\Lambda$ (характеризующее, грубо говоря, разброс собственных значений оператора $f''(x)$ ) называют числом обусловленности функции $f$ . Если $\mu >> 1$ , то функции называют плохо обусловленными или овражными. Для таких функций градиентный метод сходится медленно.

Но даже для хорошо обусловленных функций проблема выбора шага нетривиальна в силу отсутствия априорной информации о минимизируемой функции. Если шаг выбирается малым (чтобы гарантировать сходимость), то метод сходится медленно. Увеличение же шага (с целью ускорения сходимости) может привести к расходимости метода. Далее будут описаны два алгоритма автоматического выбора шага, позволяющие частично обойти указанные трудности.

Градиентный метод с дроблением шага

В этом варианте градиентного метода величина шага $\lambda^{[k]}$ на каждой итерации выбирается из условия выполнения неравенства

(2)

$f(x^{[k+1]}) = f(x^{[k]}-\lambda^{[k]} f'(x^{[k]})) \leq f(x^{[k]})-\eps \lambda^{[k]}||f'(x^{[k]})||^2$ ,

где $\eps \in (0, 1)$ - некоторая заранее выбранная константа.

Процедуру нахождения такого $\lambda^{[k]}$ обычно оформляют так. Выбирается число $\delta \in (0, 1)$ и некоторый начальный шаг $\lambda^{[0]}$ . Теперь для каждого k полагают $\lambda^{[k]}=\lambda^{[0]}$ и делают шаг градиентного метода. Если с таким $\lambda^{[k]}$ условие (2) выполняется, то переходят к следующему k. Если же (2) не выполняется, то умножают $\lambda^{[k]}$ на $\delta$ ("дробят шаг") и повторяют эту процедуру до тех пор пока неравенство (2) не будет выполняться. В условиях теоремы 1 эта процедура для каждого k за конечное число шагов приводит к нужному $\lambda^{[k]}$ .

Можно показать, что в условиях теоремы 2 градиентный метод с дроблением шага линейно сходится. Описанный алгоритм избавляет нас от проблемы выбора $\lambda^{[k]}$ на каждом шаге, заменяя ее на проблему выбора параметров $\eps,\;\delta$ и $\lambda^{[0]}$ , к которым градиентный метод менее чувствителен. При этом, разумеется, объем вычислений возрастает (в связи с необходимостью процедуры дробления шага), впрочем, не очень сильно, поскольку в большинстве задач основные вычислительные затраты ложатся на вычисление градиента.

Метод наискорейшего спуска

Рис.3 Геометрическая интерпретация метода наискорейшего спуска. На каждом шаге выбирается так, чтобы следующая итерация была точкой минимума функции на луче L.

Рис.3 Геометрическая интерпретация метода наискорейшего спуска. На каждом шаге $\lambda^{[k]}$ выбирается так, чтобы следующая итерация была точкой минимума функции $f$ на луче L.

Этот вариант градиентного метода основывается на выборе шага из следующего соображения. Из точки $x^{[k]}$ будем двигаться в направлении антиградиента до тех пор пока не достигнем минимума функции f на этом направлении, т. е. на луче $L=\{x=x^{[k]}-\lambda f'(x^{[k]});\; \lambda \leq 0}$ :

$\lambda^{[k]} = \arg\min_{ \lambda\in [0, \infty)} f(x^{[k]}-\lambda f'(x^{[k]}))$ .

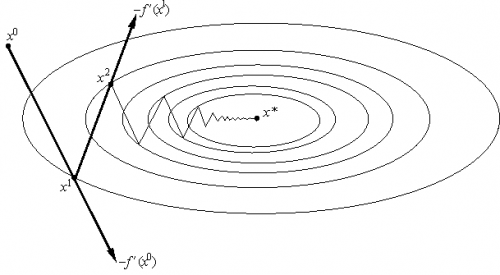
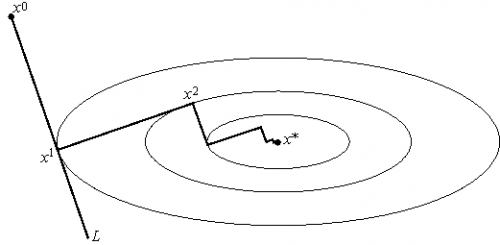
Другими словами, $\lambda^{[k]}$ выбирается так, чтобы следующая итерация была точкой минимума функции f на луче L (см. рис. 3). Такой вариант градиентного метода называется методом наискорейшего спуска. Заметим, кстати, что в этом методе направления соседних шагов ортогональны.

Метод наискорейшего спуска требует решения на каждом шаге задачи одномерной оптимизации. Практика показывает, что этот метод часто требует меньшего числа операций, чем градиентный метод с постоянным шагом.

В общей ситуации, тем не менее, теоретическая скорость сходимости метода наискорейшего спуска не выше скорости сходимости градиентного метода с постоянным (оптимальным) шагом.

Числовые примеры

Метод градиентного спуска с постоянным шагом

Для исследования сходимости метода градиентного спуска с постоянным шагом была выбрана функция:

$f(x_1,x_2)=10*x_1^2+x_2^2$ .

Начальное приближение - точка (10,10). Использован критерий останова: $||f(x^{[k+1]})-f(x^{[k]})||\leq 10^{-5}$

Результаты эксперимента отражены в таблице:

Значение шага $\lambda$	Достигнутая точность	Количество итераций
0.1	метод расходится
0.01	2e-4	320
0.001	2e-3	2648
0.0001	1e-2	20734

Из полученных результатов можно сделать вывод, что при слишком большом чаге метод расходится, при слишком малом сходится медленно и точчность хуже. Надо выбирать шаг наибольшим из тех, при которых метод сходится.

Градиентный метод с дроблением шага

Для исследования сходимости метода градиентного спуска с дроблением шага (2) была выбрана функция:

$f(x_1,x_2)=10*x_1^2+x_2^2$ .

Начальное приближение - точка (10,10). Использован критерий останова: $||f(x^{[k+1]})-f(x^{[k]})||\leq 10^{-5}$

Результаты эксперимента отражены в таблице:

Значение параметра $\eps$	Значение параметра $\delta$	Значение параметра $\lambda^{[0]}$	Достигнутая точность	Количество итераций
0.95	0.95	1	5e-4	629
0.1	0.95	1	1e-5	41
0.1	0.1	1	2e-4	320
0.1	0.95	0.01	2e-4	320

Из полученных результатов можно сделать вывод об оптимальном выборе параметров: $\eps =0.1,\; \delta=0.95,\; \lambda^{[0]}=1$ , хотя метод не сильно чувствителен к выбору параметров.

Метод наискорейшего спуска

Для исследования сходимости метода наискорейшего спуска была выбрана функция:

$f(x_1,x_2)=10*x_1^2+x_2^2$ .

Начальное приближение - точка (10,10). Использован критерий останова: $||f(x^{[k+1]})-f(x^{[k]})||\leq 10^{-5}$

Для решения одномерных задач оптимизации использован метод золотого сечения.

Метод получил точность 6e-8 за 9 итераций.

Отсюда можно сделать вывод, что метод наискорейшего спуска сходится быстрее, чем градиентный метод с дроблением шага и метод градиентного спуска с постоянным шагом.

Недостатком методом наискорейшего спуска явлляется необходимость решать одномерную задачу оптимизации.

Заключение

Методы градиентного спуска являются достаточно мощным инструментом решения задач оптимизации. Главным недостатком методов является ограниченная область применимости.

Ссылки

Список литературы

Н.Н.Калиткин. Численные методы. Москва «Наука», 1978.
Н.И.Глебов, Ю.А.Кочетов, А.В.Плясунов. Методы оптимизации. 2000.
Р.Р.Ахмеров. Методы оптимизации гладких функций.

Источник — «http://machinelearning.ru/wiki/index.php?title=%D0%9C%D0%B5%D1%82%D0%BE%D0%B4_%D0%B3%D1%80%D0%B0%D0%B4%D0%B8%D0%B5%D0%BD%D1%82%D0%BD%D0%BE%D0%B3%D0%BE_%D1%81%D0%BF%D1%83%D1%81%D0%BA%D0%B0»

Категория: Учебные задачи

Метод градиентного спуска

Материал из MachineLearning.

Содержание

Введение

Метод градиентного спуска

Идея метода

Алгоритм

Критерий останова

Сходимость градиентного спуска с постоянным шагом

Выбор оптимального шага

Градиентный метод с дроблением шага

Метод наискорейшего спуска

Числовые примеры

Метод градиентного спуска с постоянным шагом

Градиентный метод с дроблением шага

Метод наискорейшего спуска

Рекомендации программисту

Заключение

Ссылки

Список литературы

Просмотры

Личные инструменты

Навигация

Поиск

Инструменты