Группировка категорий и сегментация признаков в логистической регрессии (пример)

Материал из MachineLearning.

Версия от 18:17, 31 октября 2010; Nkzh (Обсуждение | вклад)

(разн.) ← Предыдущая | Текущая версия (разн.) | Следующая → (разн.)

Группировка категорий и сегментация признаков — методы, позволяющие упростить и одновременно улучшить регрессионную модель. В частности, группировка категорий позволяет понять взаимосвязь значений признаков и использовать линейные модели для нелинейных зависимостей.

Постановка задачи

Дана задача кредитного скоринга. Регрессионная модель - логистическая регрессия. Требуется найти множество активных признаков. Затем сегментировать линейные признаки, сгруппировать номинальные и ординарные. При этом надо применить как новые алгоритмы, так и классические. Сравнить оба подхода, вычислить статистическую значимость производных признаков.

Описание данных

Используются реальные данные (GERMAN_UIC) о выдаче или не выдаче банком кредитов. Всего приведены 24 признака для 1000 человек и информация о том, выдан ли впоследствии кредит. Формально данные можно представить следующим образом:

Набор данных: $\mathbf{x}\in\mathbb{R}^{n},\ y\in\mathbb{R}$

$\mathbf{D} = \{(\mathbf{x}^{1},y^{1}),\ldots,(\mathbf{x}^{i},y^{i}),\ldots,(\mathbf{x}^{m},y^{m})\}$

Целевая переменная: $\mathbf{y} = (y^{1},\ldots,y^{m})^{T}$

Модель: $P(y^{i}|\mathbf{x}^i) = (\sigma(\langle\mathbf{w},\mathbf{x}^{i}\rangle))^{y^{i}}(1 - \sigma(\langle\mathbf{w},\mathbf{x}^{i}\rangle))^{1 - y^{i}}\$ где $\sigma(\langle\mathbf{w},\mathbf{x}^{i}\rangle) = \frac{1}{1 + \exp(-\langle\mathbf{w},\mathbf{x}^{i}\rangle)}$

Индексы: $\{1,\ldots,m\} = \mathbf{L}\cup\mathbf{T}$ - разбиение на обучающую и контрольную выборки. $\{1,\ldots,n\} = \mathbf{F}$ - индексы признаков.

Описание алгоритмов

Поиск активных признаков

Сначала находится множество активных признаков. Для этого решается задача максимизации правдоподобия, или эквивалентно - минимизация его логарифма, взятого с противополжным знаком

$-\ln(P(\mathbf{y}|\mathbf{x})) = - \sum_{i\subseteq\mathbf{L}}(y^{i}\ln(\sigma(\langle\mathbf{w},\mathbf{x}^{i}\rangle)) + (1 - y^{i})\ln(1 - \sigma(\langle\mathbf{w},\mathbf{x}^{i}\rangle))) = S_{\mathbf{L},\mathbf{A}}(\mathbf{w})$

Здесь под строкой $\mathbf{x}^{i}$ подразумевается строка из условия, но с удаленными координатами, номера которых не входят во множество индексов $A$ . Вектор $\mathbf{w}$ соответствующей длины. Множество активных признаков - $\mathbf{A}\subseteq\mathbf{F}$ . Тогда задача нахождения множества активных признаков и соответствующего им вектора весов записывается в виде

$\mathbf{w}_{\mathbf{A}} = \underset{\mathbf{w}}{\operatorname{argmin}}(S_{\mathbf{L},\mathbf{A}}(\mathbf{w}))$

$\mathbf{A} = \underset{\mathbf{A}^{*}\in2^{\mathbf{F}}}{\operatorname{argmin}}(S_{\mathbf{T},\mathbf{A}^{*}}(\mathbf{w}__{\mathbf{A}^{*}}))$

Для решения задачи поиска множества активных признаков предлагается следующий подход. Все линейные признаки заведомо считаются активными. В данном случае их всего 3, и впоследствии они будут сегментированы. Далее используется простой жадный алгоритм, удаляющий на каждом шаге признак, без которого значение правдоподобия наиболее оптимально. В логистической регрессии добавляется постоянный признак, а вектор весов находится с помощью алгоритма Ньютона - Рафсона. В данном эксперименте считается, что удаленными должны быть около половины всех признаков.

Сегментация линейных признаков

Пусть значения линейного признака $\mathbf{x}_{i}$ характеризуются числами из отрезка $[a_{i},b_{i}]$ . Вводится разбиение отрезка $[a_{i},b_{i}]$ , на $k$ отрезков одинаковой длины $a_{i} = x_{1} < x_{2} < \ldots < x_{n_{k}} = b_{i}$ . Строится кусочно - линейная функция $f(x) = a x+ b + c_1|x-x_1| + c_2|x-x_2| + \ldots +c_n|x-x_n|$ . Значения признака - значение функции в соответствующей точке отрезка $[a_{i},b_{i}]$ . Коэффициенты $f(x)$ подобираются так, чтобы $f(x_{2m - 1}) = 0,\ f(x_{2m}) = 1$ где $m\in\mathbb N$ . На каждом шаге алгоритма случайным образом изменяется значение $x_{i}$ , но так, чтобы не изменить порядок чисел разбиения. Коэффициенты $f(x)$ изменяются соответсвующим образом. Если для новой функции $f(x)$ значение $S_{\mathbf{L},\mathbf{A}}(\mathbf{w})$ уменьшается, то сохраняется изменение $x_{i}$ . Алгоритм заканчивает работу по достижении первого минимума.

Группировка категорий

Пусть номинальный признак $\mathbf{x}_{i}$ характеризуются числами из множества категорий $\tex\{1,\ldots,c\}$ . Ему в соответствие ставится множество $\Gamma$ такое, что $1 \le |\Gamma| \le c$ . Требуется найти такую сюръективную функцию $h_{\Gamma}:\{1,\ldots,c\}\to\Gamma$ и соответствующее ей множество $\Gamma = \{1,\ldots,c^{*}\}$ , которая минимизирует функцию $S_{\mathbf{T},\mathbf{A}(\mathbf{w})$ при замене для $\mathbf{x}_{i}$ : $\tex\{1,\ldots,c\}$ на $\tex\{h_{\Gamma}(1),\ldots,h_{\Gamma}(c)\}$ . В данном случае признаков и категорий достаточно мало, поэтому эффективен полный перебор.

Также предлагается один из классических методов группировки категорий. Для этого сначала для каждого значения номинального признака считается его $WOE$ (Weight of evidence) по формуле: $WOE = 100* \ln(\frac{Distr Good}{Distr Bad})$ , где $Distr Good$ в данном случае - отношение числа людей, которым выдали кредит, имевших данное значение номинального признака, к общему числу людей, которым выдали кредит. $Distr Bad$ - отношение числа людей, которым не выдали кредит, имевших данное значение номинального признака, к общему числу людей, которым не выдали кредит. Теперь пусть некоторый номинальный признак под номером $j$ принимает значения $\tex\{1,\ldots,n_{j}\}$ . Для него нужно рассчитать $IV$ (Information Value) по формуле: $IV = \sum_{i = 1}^{n_j}(Distr Good_{i} - Distr Bad_{i})* \ln(\frac{Distr Good_{i}}{Distr Bad_{i}})$ . Для признаков с самыми большими значениями $IV$ в одну группу объединяются категории с близкими значеними $WOE$ . При таком подходе важно задать условия близости значений $WOE$ и количество группируемых категорий.

Вычислительный эксперимент

Визуализация результатов

Результат выполнения алгоритма поиска множества активных признаков. Линейные признаки для удобства перенесены в начало списка.

Активные признаки.
1, 2, 3, 4, 5, 6, 7, 9, 10, 11 , 12, 16, 20

Примеры сегментации линейных признаков

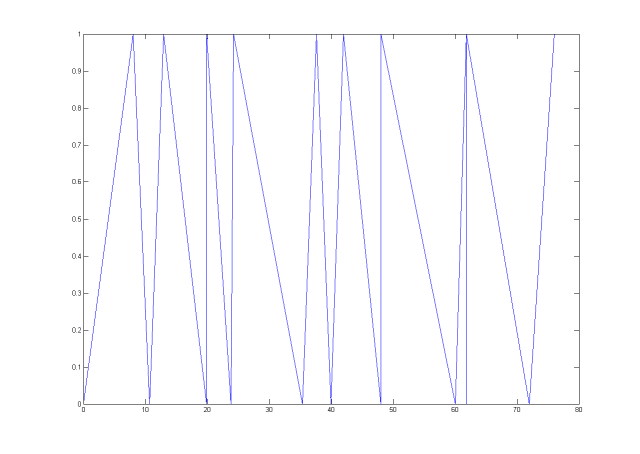
Изображен график функции $f(x)$ .

Признак номер 1. Начальная длина шага равна 8.

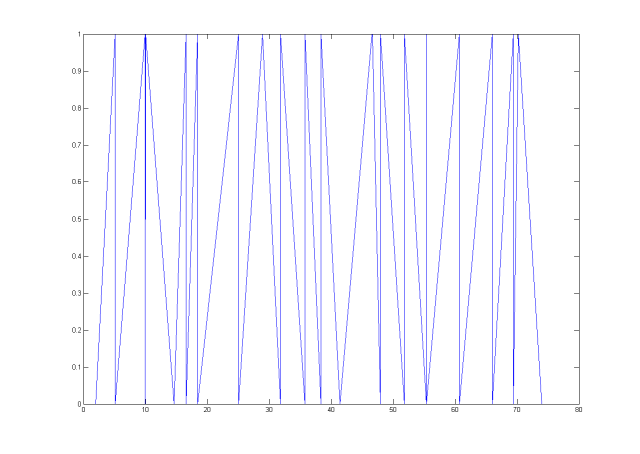
Признак номер 1. Начальная длина шага равна 4.

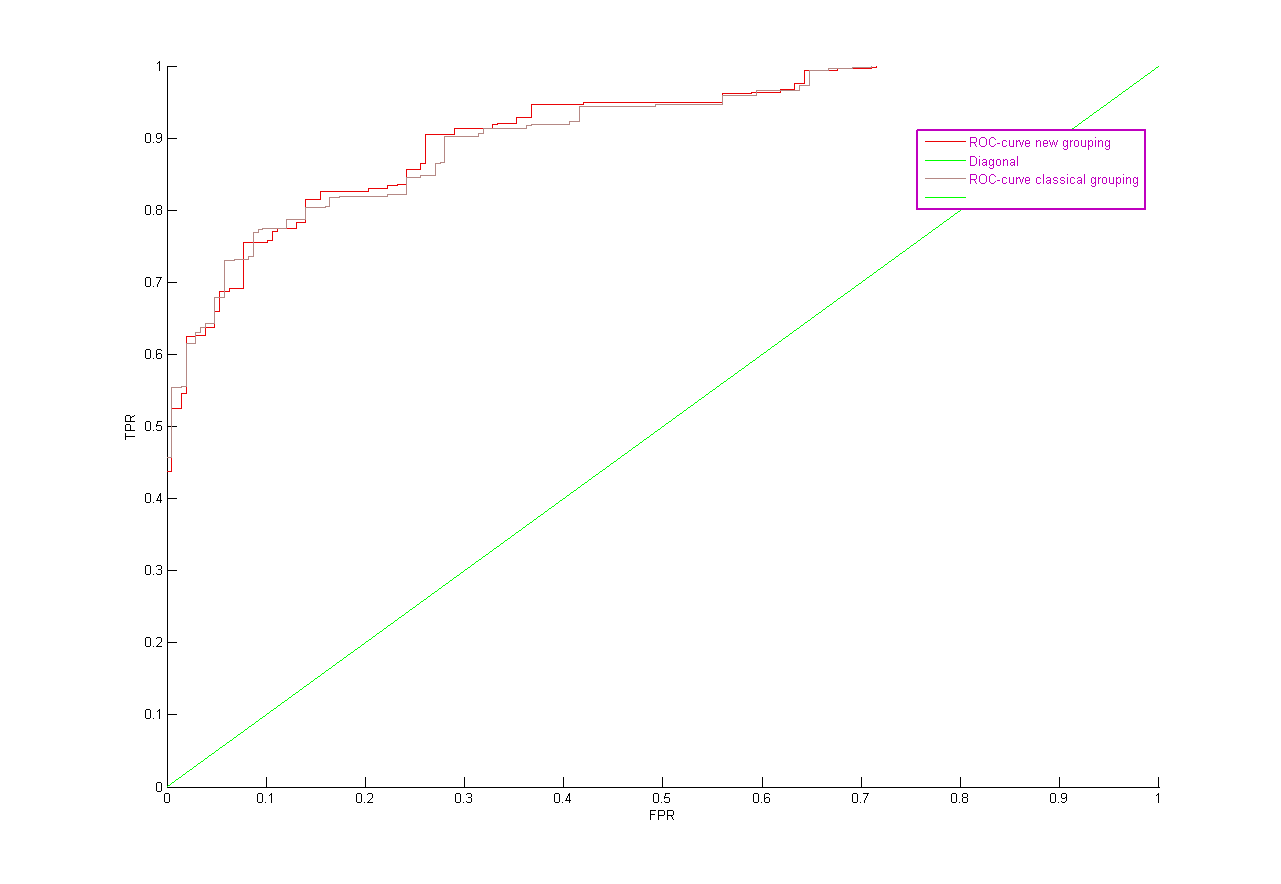
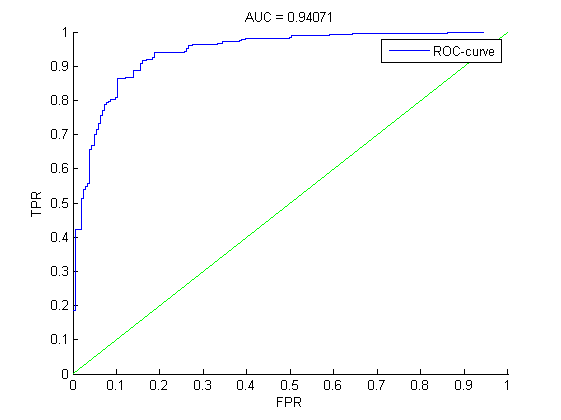
ROC - кривые

В случае группировки перебором.

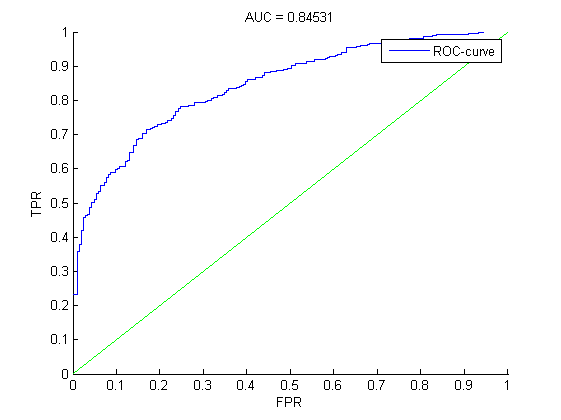
Классическая группировка. С условием близости Weight of evidence равным 10. Дискретизация меньше , так как число групп больше чем в предыдущем случае.

С условием близости Weight of evidence равным 5.

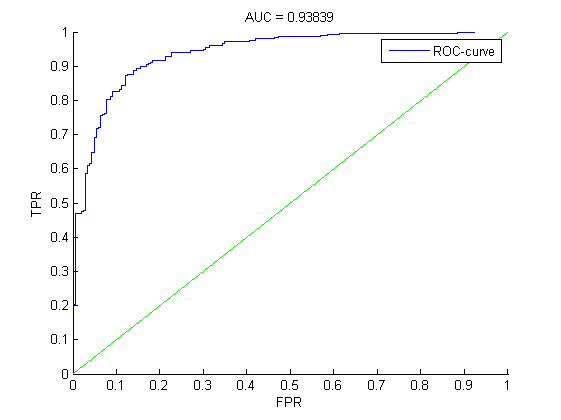
Сегментация линейных признаков. Шаг функции $f(x)$ равен 2. Значения сильно изменяются, так как в группировке категорий линейные признаки были исключены.

Исследование свойств алгоритма

Значения Information Value для номинальных признаков

4	5	6	7	9	10	11	12	16	20
0.6670	0.2092	0.1960	0.0864	0.0036	0.1126	0.0576	0.0133	0.0322	0.0314

Значения S(w) на контрольной выборке

Сегментация линейных	Классическая группировка	Альтернативная группировка
123.2138	158.1518	145.6036

S(w) на контроле принимает наилучшее значение при сегментации линенйных признаков. Переборная группировка дает несколько лучшее по сравнению с классикой значение S(w) на контроле, зато сама модель несколько хуже, чем в классическом случае с точки зрения значения AUC.

Исходный код

Исходный код Matlab

Смотри также

Литература

Siddiqi N. Credit Risk Scorecards: Developing and Implementing Intelligent Credit Scoring. John Wiley & Sons, Inc. 2006
Bishop C. Pattern Recognition And Machine Learning. Springer. 2006.

Данная статья является непроверенным учебным заданием.

Студент: Участник:Никита Животовский

Преподаватель: Участник:В.В. Стрижов

Срок: ?

До указанного срока статья не должна редактироваться другими участниками проекта MachineLearning.ru. По его окончании любой участник вправе исправить данную статью по своему усмотрению и удалить данное предупреждение, выводимое с помощью шаблона {{Задание}}.

См. также методические указания по использованию Ресурса MachineLearning.ru в учебном процессе.

Источник — «http://machinelearning.ru/wiki/index.php?title=%D0%93%D1%80%D1%83%D0%BF%D0%BF%D0%B8%D1%80%D0%BE%D0%B2%D0%BA%D0%B0_%D0%BA%D0%B0%D1%82%D0%B5%D0%B3%D0%BE%D1%80%D0%B8%D0%B9_%D0%B8_%D1%81%D0%B5%D0%B3%D0%BC%D0%B5%D0%BD%D1%82%D0%B0%D1%86%D0%B8%D1%8F_%D0%BF%D1%80%D0%B8%D0%B7%D0%BD%D0%B0%D0%BA%D0%BE%D0%B2_%D0%B2_%D0%BB%D0%BE%D0%B3%D0%B8%D1%81%D1%82%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%BE%D0%B9_%D1%80%D0%B5%D0%B3%D1%80%D0%B5%D1%81%D1%81%D0%B8%D0%B8_%28%D0%BF%D1%80%D0%B8%D0%BC%D0%B5%D1%80%29»

Категории: Непроверенные учебные задания | Учебные материалы