Медиальное множество

Материал из MachineLearning.

Версия от 21:51, 27 февраля 2011; Иван Мехедов (Обсуждение | вклад)
(разн.) ← Предыдущая | Текущая версия (разн.) | Следующая → (разн.)
Перейти к: навигация, поиск

Содержание

Определение

Для каждой точки x\in\Omega обозначим D(x) множество ближайших граничных точек: D(x)=\{y\in\Omega^c: d(x,y)=d(x,\Omega^c)\} (\Omega^c = \mathbb{R}^n\setminus\Omega --- дополнение к \Omega).

Медиальным множеством (medial locus) \Omega называется множество M_{\Omega} точек \Omega, имеющих, по меньшей мере, две ближайшие граничные точки: M_{\Omega}=\{x\in\Omega|Card(D(x))\geq 2\}.

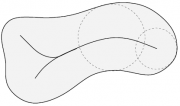
Медиальное множество (срединная ось) на плоскости

Зачастую медиальное множество называется срединной осью (medial axis), хотя лучше такое название применять только к плоским множествам (\Omega\subset \mathbb{R}^2), особенно в русскоязычной терминологии.

В случае, когда n=2, обычно рассматривают не произвольные открытые ограниченные связные множества \Omega, а накладывают определенные ограничения на границу \Omega^c. Множество \overline{\Omega} при этом называется плоской фигурой.

Медиальное множество плоской фигуры называют также срединной осью (medial axis) плоской фигуры.

Медиальное множество (срединная ось) плоской фигуры
Медиальное множество (срединная ось) плоской фигуры

Внутреннее и внешнее медиальное множество, множество симметрии

Строго говоря, определенное выше медиальное множество является внутренним медиальным множеством множества \Omega (internal medial locus). Иногда рассматривают также внешние медиальные множества.

Для каждой точки x\in\Omega^c обозначим D_e(x) множество ближайших граничных точек: D_e(x)=\{y\in\Omega^c: d(x,y)=d(x,\Omega)\}.

Внешним медиальным множеством \Omega (external medial locus) называется множество M^e_{\Omega} точек \Omega^c, имеющих, по меньшей мере, две ближайшие граничные точки: M^e_{\Omega}=\{x\in\Omega^c|Card(D_e(x))\geq 2\}.

Внутреннее медиальное множество обозначается M^i_\Omega. Иногда под термином медиальное множество понимают объединение внутреннего и внешнего медиальным множеств: M_{\Omega}=M^i_{\Omega}\cup M^e_{\Omega}, но чаще всего медиальное множество --- это именно внутреннее медиальное множество: M_{\Omega}=M^i_{\Omega}.

Для каждой точки x\in\mathbb{R}^n обозначим D_{sym}(x) множество ближайших точек границы : <tex>D_{sym}(x)=\{y\in\partial\Omega^c: d(x,y)=d(x,\partial\Omega^c)\}.

Множеством симметрии \Omega (symmetry set) называется множество Sym_{\Omega} точек \mathbb{R}^n, имеющих, по меньшей мере, две ближайшие точки на границе : <tex>Sym_{\Omega}=\{x\in\mathbb{R}^n|Card(D_{sym}(x))\geq 2\}.

Связь между медиальным и центральным множествами

Для любого связного открытого ограниченного множества \Omega\subset\mathbb{R}^n верно, что его медиальное множество является подмножеством его центрального множества: M_{\Omega}\subseteq S_{\Omega} .

При n=2, <tex> M_{\Omega}=S_{\Omega} , если \Omega --- многоугольная фигура.

См. также

Литература

  • Chazal F., Soufflet R. Stability and finiteness properties of Medial Axis and Skeleton // Journal of Dynamic and Control Systems, Vol. 10, No.2, 2004. pp. 149 -- 170. [1]
  • Siddiqi K., Pizer K. Medial Representations: Mathematics, Algorithms, Applications, Springer, 2008.
Источник — «http://machinelearning.ru/wiki/index.php?title=%D0%9C%D0%B5%D0%B4%D0%B8%D0%B0%D0%BB%D1%8C%D0%BD%D0%BE%D0%B5_%D0%BC%D0%BD%D0%BE%D0%B6%D0%B5%D1%81%D1%82%D0%B2%D0%BE»
Личные инструменты