Статистический анализ данных (курс лекций, К.В.Воронцов)/2011, ФУПМ

Материал из MachineLearning.

Версия от 16:32, 8 марта 2011; Riabenko (Обсуждение | вклад)

(разн.) ← Предыдущая | Текущая версия (разн.) | Следующая → (разн.)

Содержание

1 Задание 1. Исследование свойств одномерных статистических методов на модельных данных
- 1.1 Пример задания
- 1.2 Задания
  - 1.2.1 Устойчивость критериев к нарушению предположений
  - 1.2.2 Влияние связок на поведение статистических критериев
2 Литература
3 Ссылки

Задание 1. Исследование свойств одномерных статистических методов на модельных данных

Необходимо провести исследование одной или нескольких классических статистических техник. В соответствии с индивидуальными параметрами задания необходимо указанным способом сгенерировать одну или несколько выборок из заданного распределения, применить исследуемые статистические методы, а затем многократно повторить эту процедуру для различных значений параметров. По результатам расчётов необходимо построить требуемые в задании графики и сделать выводы.

Пример задания

Исследуем поведение классического двухвыборочного критерия Стьюдента для проверки гипотезы однородности против альтернативы сдвига при разных значениях параметров.

$x^n = (x_1,\ldots,x_n)\sim N(\mu_1,\sigma),\;\; y^n = (y_1,\ldots,y_n)\sim N(\mu_2,\sigma);$

$H_0\,:\; \mu_1=\mu_2,$

$H_1\,:\; \mu_1\neq\mu_2.$

$\sigma = 1; \;\;\; \mu_1=0; \;\;\; \mu_2=0\,:\,0.05\,:\,3; \;\;\; n=5\,:\,1\,:\,50.$

При каждом значении $\mu_2$ выборки для разных значений $n$ генерируются независимо.

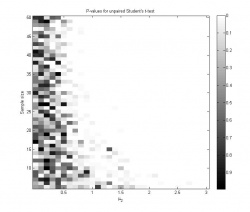
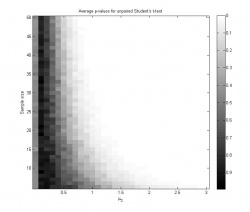
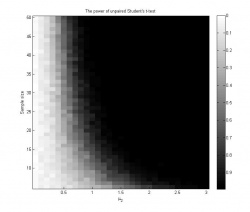
Графики 1 и 2 иллюстрируют зависимость достигаемого уровня значимости от размера выборки и среднего $\mu_2$ . На графике 3 показана зависимость мощности критерия от параметров задачи; мощность в каждой точке оценивается как доля экспериментов, в которых гипотеза была отвергнута на уровне значимости $\alpha=0.05$ .

График 1: значения достигаемого уровня значимости при однократной генерации выборок.

График 2: значения достигаемого уровня значимости, усрёднённые по 100 экспериментам.

График 3: значения эмпирических оценок мощности критерия при проведении 100 экспериментов ( $\alpha=0.05$ ).

Видно, что при $\mu_2=0$ среднее значение достигаемого уровня значимости при многократном повторении эксперимента равно 0.5 для любого размера выборки. Это логично, так как при $\mu_2=0$ нулевая гипотеза справедлива, и достигаемый уровень значимости имеет равномерное распределение на $[0,1].$
При $n>20$ и $\mu_2>1$ критерий имеет достаточную мощность, и нулевая гипотеза чаще всего отвергается.
При размере выборки до 50 элементов и среднем второй выборки $\mu_2<0.5$ критерий практически не способен отклонить гипотезу однородности, мощность в этой области изменения параметров низка.
При большой разнице между средними выборок $(\mu_2>2)$ критерий достаточно уверенно отвергает гипотезу однородности даже на выборках небольшого размера (5-6 элементов).

Задания

Устойчивость критериев к нарушению предположений

Исследовать устойчивость двухвыборочного критерия Стьюдента для независимых выборок к нарушению предположения о нормальности данных.

$x^n \sim p_1\cdot N(\mu_1,1)+ \left(1-p_1\right)\cdot U\left[-a+\mu_1,a+\mu_1\right]$ — выборка длины $n$ из смеси нормального $N(\mu_1,1)$ и равномерного $U\left[-a+\mu_1,a+\mu_1\right]$ распределений с весами $p_1$ и $1-p_1$ соответственно (при генерации выборки используется случайный датчик — если его значение не превосходит $p_1$ , то добавляем в выборку элемент, взятый из нормального распределения, иначе — элемент, взятый из равномерного).
$y^n \sim p_2\cdot N(\mu_2,1)+ \left(1-p_2\right)\cdot U\left[-a+\mu_2,a+\mu_2\right]$ — аналогичная выборка.
$H_0\,:\; \mu_1=\mu_2, \;\; H_1\,:\; \mu_1\neq\mu_2;$
$\mu_1=0; \;\; \mu_2=-1\,:\,0.05\,:\,1.$
Построить графики вида 1, 2, 3, сделать выводы о чувствительности критерия к зашумлению одной из выборок.

Кононенко Даниил: $p_1=0.8; \;\; p_2=1, \;\; a=1; \;\; n=15\,:\,5\,:\,200.$

Голкин Александр: $p_1=0.9; \;\; p_2=1, \;\; a=5; \;\; n=15\,:\,5\,:\,200.$

Завадский Глеб: $p_1=p_2=0.8; \;\; a=1; \;\; n=15\,:\,5\,:\,200.$

Чугунов Кирилл: $p_1=p_2=0.9; \;\; a=5; \;\; n=15\,:\,5\,:\,200.$

Корниенко Алексей: $p_1=p_2=0\,:\,0.01\,:\,1; \;\; a=1; \;\; n=150.$

Кузнецов Михаил: $p_1=p_2=0\,:\,0.01\,:\,1; \;\; a=5; \;\; n=100.$

Исследовать устойчивость критерия Фишера для проверки равенства дисперсий к нарушению предположения о нормальности выборок.

$x^n \sim p_1\cdot N(0,\sigma_1)+ \left(1-p_1\right)\cdot U\left[-a,a\right]$ — выборка длины $n$ из смеси распределений $N(0,\sigma_1)$ и $U[-a,a]$ с весами $p_1$ и $1-p_1$ соответственно (при генерации выборки используется случайный датчик — если его значение не превосходит $p_1$ , то добавляем в выборку элемент, взятый из нормального распределения, иначе — элемент, взятый из равномерного).
$y^n \sim p_2\cdot N(0,\sigma_2)+ \left(1-p_2\right)\cdot U\left[-a,a\right]$ — аналогичная выборка.
$H_0\,:\; \sigma_1=\sigma_2, \;\; H_1\,:\; \sigma_1\neq\sigma_2.$
$\sigma_1=1, \;\; \sigma_2=0.1\,:\,0.1\,:\,4.$
Построить графики вида 1, 2, 3, сделать выводы о чувствительности критерия к зашумлению.

Иванов Николай: $p_1=0.8; \;\; p_2=1, \;\; a=1; \;\; n=15\,:\,5\,:\,200.$

Рубцов Александр: $p_1=0.9; \;\; p_2=1, \;\; a=5; \;\; n=15\,:\,5\,:\,200.$

Рукина Дарья: $p_1=p_2=0.8; \;\; a=1; \;\; n=15\,:\,5\,:\,200.$

Савгиров Арш: $p_1=p_2=0.9; \;\; a=5; \;\; n=15\,:\,5\,:\,200.$

Спиридонов Роман: $p_1=p_2=0\,:\,0.01\,:\,1; \;\; a=1; \;\; n=150.$

Стукалюк Владимир: $p_1=p_2=0\,:\,0.01\,:\,1; \;\; a=5; \;\; n=100.$

Влияние связок на поведение статистических критериев

Исследовать влияние совпадающих элементов выборки на статистические критерии, проверяющие гипотезу нормальности.

$H_0\,:\; x^n$ распределена нормально; $H_1\,:\; x^n$ распределена по какому-то другому закону.
Для генерации выборки со связками может использоваться округление элементов выборки, либо следующая процедура:

генерируется выборка размера $n$ из исходного распределения: $x^n\sim p\cdot N\left(0,1\right)+\left(1-p\right)U\left[a,b\right];$
в вариационном ряду выборки $x^n_{\left(i\right)}$ выбираются $k$ непересекающихся пар элементов $\left(x_{\left(i\right)}, x_{\left(i+1\right)}\right)$ , лежащих ближе всего друг к другу;
для всех $k$ выбранных пар элементы выборки $x_{\left(i\right)}$ и $x_{\left(i+1\right)$ заменяются их средним.