Статистический анализ данных (курс лекций, К.В.Воронцов)/2011

Материал из MachineLearning.

Версия от 19:29, 2 октября 2011; Riabenko (Обсуждение | вклад)

(разн.) ← Предыдущая | Текущая версия (разн.) | Следующая → (разн.)

Содержание

1 Задание 1. Исследование свойств одномерных статистических критериев на модельных данных
- 1.1 Пример задания
- 1.2 Задания
2 Литература
3 Ссылки

Задание 1. Исследование свойств одномерных статистических критериев на модельных данных

Необходимо провести исследование одного или нескольких классических критериев проверки статистических гипотез. Интерес представляет поведение достигаемого уровня значимости (p-value) как функции размера выборок и параметров распределения. В соответствии с индивидуальными параметрами задания необходимо указанным способом сгенерировать одну или несколько выборок из заданного распределения, выполнить проверку гипотезы при помощи соответствующего критерия, а затем многократно повторить эту процедуру для различных значений параметров. По результатам расчётов необходимо построить требуемые в задании графики, среди которых могут быть следующие:

график зависимости достигаемого уровня значимости от значений параметров при однократном проведении эксперимента;
график зависимости достигаемого уровня значимости одного или двух критериев от значений параметров, усреднённого по большому количеству повторений эксперимента (например, по 1000 повторений);
график с эмпирическими оценками мощности одного или двух критериев для разных значений параметров.

В качестве оценки мощности принимается доля отвержений нулевой гипотезы среди всех проверок. То есть, если эксперимент повторялся $k$ раз для каждого набора значений параметра, и в $m$ из $k$ случаев гипотеза была отвергнута на некотором фиксированном уровне значимости $\alpha$ (примем $\alpha=0.05$ ), оценкой мощности будет отношение $m/k$ .

Необходимо сдать: выполненный в LaTex или Microsoft Word отчёт с описанием алгоритма, построенными графиками и выводами (объяснение полученных результатов моделирования, границы применимости критерия и т.д.), а также *.m-файл или R-скрипт, при запуске которого на экран выводятся графики, соответствующие имеющимся в отчёте.

Задание принимается до первого ноября.

Пример задания

Исследуем чувствительность классического двухвыборочного критерия Стьюдента для проверки гипотезы однородности против альтернативы сдвига при зашумлении выборок наблюдениями, взятыми из равномерного распределения.

$x^n, \;\; x \sim 0.9\cdot N(\mu_1,1)+ 0.1\cdot U\left[-5+\mu_1,5+\mu_1\right]$ — выборка длины $n$ из смеси стандартного нормального $N(\mu_1,1)$ и равномерного $U\left[-5+\mu_1,5+\mu_1\right]$ распределений с весами $0.9$ и $0.1$ соответственно (при генерации выборки используется случайный датчик — если его значение не превосходит $0.9$ , то добавляем в выборку элемент, взятый из нормального распределения, иначе — элемент, взятый из равномерного).

$y^n, \;\; y \sim 0.9\cdot N(\mu_2,1)+ 0.1\cdot U\left[-5+\mu_2,5+\mu_2\right]$ — аналогичная выборка.

$H_0\,:\; \mathbb{E}(x)=\mathbb{E}(y), \;\; H_1\,:\; \mathbb{E}(x)\neq\mathbb{E}(y).$

$\mu_1=0, \;\; \mu_2=-2\,:\,0.01\,:\,2, \;\; n=15\,:\,5\,:\,200.$

При каждом значении $\mu_2$ выборки для разных значений $n$ генерируются независимо.

Значения достигаемого уровня значимости при однократной генерации выборок.

Значения достигаемого уровня значимости, усрёднённые по 3000 экспериментам.

Значения эмпирических оценок мощности критерия при проведении 3000 экспериментов ( $\alpha=0.05$ ).

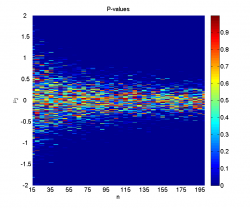
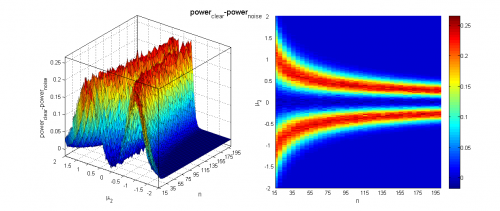
Заметим, что однократная генерация выборок даёт достаточно нестабильные результаты, не позволяя точно оценить границы области, где нулевая гипотеза отклоняется, поэтому и необходимо усреднение по большому числу экспериментов.

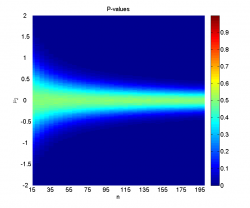
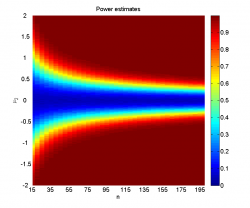
Видно, что при достаточно большой разнице между средними и большом размере выборок наличие шума не мешает уверенно отклонять гипотезу однородности. Когда, наоборот, разница между средними невелика (меньше 0.2-0.5 в зависимости от размера выборок), мощность близка к нулю, а среднее достигаемого уровня значимости колеблется около 0.5, что логично, так как его распределение при справедливости нулевой гипотезы равномерно на $[0,1]$ .

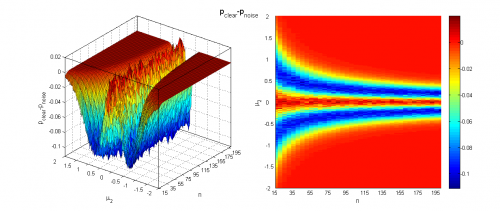
Чтобы оценить вклад зашумления выборок, оценим при всех значениях параметра мощность критерия и средний достигаемый уровень значимости на аналогичных выборках без шума и сравним результаты.

Разность средних достигаемых уровней значимости на выборках без шума и с шумом.

Разность эмпирических оценок мощности на выборках без шума и с шумом.

Видно, что наличие шума всё меньше влияет на работу критерия с ростом объёма выборок и разницы между их средними. Тем не менее, в некоторых областях изменения параметров потеря мощности из-за 10% зашумления может составлять до 20%, а средний достигаемый уровень значимости может быть выше на 0.1.

Отметим, что приведённые количественные выводы справедливы только для шума рассматриваемой структуры.

Задания

Анализ чувствительности критериев к редактированию выборки

Известно, что исключение из выборки определённых наблюдений зачастую может достаточно сильно повлиять на результат анализа. Необходимо исследовать чувствительность указанного критерия к редактированию выборки, построить графики, сделать выводы.

На каждом шаге генерируются выборки исходной длины, проводится проверка гипотезы $H_0$ , затем по некоторому правилу из указанной выборки исключается один из элементов, проверка гипотезы повторяется, затем исключается ещё один, и т.д. Обозначим за $k$ максимальное число исключённых в таком процессе элементов; примем во всех задачах $k=50$ .

Двухвыборочный критерий Стьюдента для связных выборок.

$x^n,\;\; x \sim N(0,1), y^n=x^n+z^n, \;\; z \sim N(\mu,\sigma^2),$
$H_0\,:\; \mathbb{E}(x)=\mathbb{E}(y), \;\; H_1\,:\; \mathbb{E}(y)> \mathbb{E}(x).$

Алешина Мария: $n=100,\;\;\sigma=1,\;\;\mu=-1\,:\,0.01\,:\,1,\;\;$ на каждом шаге исключается пара наблюдений $x_i, y_i,$ разность которых максимальна.

Антипов Григорий: $n=150,\;\;\sigma=2,\;\;\mu=-1\,:\,0.01\,:\,1,\;\;$ на каждом шаге исключается пара наблюдений $x_i, y_i,$ разность которых минимальна.

Критерий Уилкоксона-Манна-Уитни для независимых выборок.

$x^n,\;\; x \sim N(0,1), y^n, \;\; y \sim N(\mu,\sigma^2),$
$H_0\,:\; \mathbb{E}(x)=\mathbb{E}(y), \;\; H_1\,:\; \mathbb{E}(y)> \mathbb{E}(x).$

Батурина Вера: $n=100,\;\;\sigma=1,\;\;\mu=-1\,:\,0.01\,:\,1,\;\;$ на каждом шаге исключается максимальный элемент выборки $y^n$ .

Бондаренко Николай: $n=150,\;\;\sigma=2,\;\;\mu=-1\,:\,0.01\,:\,1,\;\;$ на каждом шаге исключается максимальный элемент выборки $x^n$ .

Валов Дмитрий: $n=200,\;\;\sigma=4,\;\;\mu=-1\,:\,0.01\,:\,1,\;\;$ на каждом шаге исключается минимальный элемент выборки $x^n$ .

Критерий Фишера для проверки равенства дисперсий.

$x^n, \;\; x \sim N(0,1), y^n, \;\; y \sim N(0,\sigma^2),$
$H_0\,:\; var(x)=var(y), \;\; H_1\,:\; var(y)> var(x).$

Головин Антон: $n=100,\;\;\sigma=0.01\,:\,0.01\,:\,2,\;\;$ на каждом шаге исключается максимальный по модулю элемент выборки $y^n$ .

Дударенко Мария: $n=200,\;\;\sigma=0.01\,:\,0.01\,:\,2,\;\;$ на каждом шаге исключается минимальный по модулю элемент выборки $y^n$ .

Исупова Ольга: $n=100,\;\;\sigma=0.01\,:\,0.01\,:\,2,\;\;$ на каждом шаге исключается максимальный элемент выборки $y^n$ .

Касперский Иван: $n=200,\;\;\sigma=0.01\,:\,0.01\,:\,2,\;\;$ на каждом шаге исключается минимальный элемент выборки $y^n$ .

Устойчивость критериев к нарушению предположения нормальности

Исследовать поведение параметрических критериев, предполагающих нормальность данных, при зашумлении выборок наблюдениями, взятыми из равномерного распределения.

Двухвыборочный критерий Стьюдента для связных выборок

$x^n, \;\; x \sim N(0,1),$
$y^n=x^n+z^n, \;\; z \sim p\cdot N(\mu,\sigma^2) + \left(1-p\right)\cdot U\left[-a+\mu, a+\mu\right]$ — связанная с ней выборка, полученная добавлением компоненты $z$ из смеси нормального $N(\mu,\sigma^2)$ и равномерного $U[-a+\mu,a+\mu]$ распределений с весами $p$ и $1-p$ соответственно (при генерации выборки используется случайный датчик — если его значение не превосходит $p$ , то добавляем в выборку элемент, взятый из нормального распределения, иначе — элемент, взятый из равномерного),
$H_0\,:\; \mathbb{E}(x)=\mathbb{E}(y), \;\; H_1\,:\; \mathbb{E}(x)\neq \mathbb{E}(y).$

Колев Денис: $a=1, \;\; n=100, \;\; \sigma=0.5, \;\; p=0\,:\,0.01\,:\,1, \;\; \mu=0\,:\,0.03\,:\,3.$

Колесников Александр: $a=3, \;\; n=100, \;\; \sigma=0.5, \;\; p=0\,:\,0.01\,:\,1, \;\; \mu=0\,:\,0.03\,:\,3.$

Макарова Елена: $a=3, \;\; n=100, \;\; \sigma=0.01\,:\,0.01\,:\,1, \;\; p=0.8, \;\; \mu=0\,:\,0.03\,:\,3.$

Критерий Фишера для проверки равенства дисперсий.

$x^n, \;\; x \sim p_1\cdot N(0,\sigma_1^2)+ \left(1-p_1\right)\cdot U\left[-a,a\right]$ — выборка длины $n$ из смеси нормального $N(0,\sigma_1^2)$ и равномерного $U[-a,a]$ распределений с весами $p_1$ и $1-p_1$ соответственно (при генерации выборки используется случайный датчик — если его значение не превосходит $p_1$ , то добавляем в выборку элемент, взятый из нормального распределения, иначе — элемент, взятый из равномерного),
$y^n,\;\; y \sim p_2\cdot N(0,\sigma_2^2)+ \left(1-p_2\right)\cdot U\left[-a,a\right]$ — аналогичная выборка,
$H_0\,:\; var(x)=var(y), \;\; H_1\,:\; var(x)\neq var(y),$
$\sigma_1=2, \;\; \sigma_2=0.1\,:\,0.05\,:\,4.$

Миняйлов Владимир: $p_1=p_2=0.8, \;\; a=2, \;\; n=15\,:\,5\,:\,200.$

Молчанов Андрей: $p_1=p_2=0\,:\,0.01\,:\,1, \;\; a=2, \;\; n=150.$

Онищенко Алина: $p_1=p_2=0\,:\,0.01\,:\,1, \;\; a=3, \;\; n=100.$

Анализ поведения разновидностей критерия Стьюдента

Критерий Стьюдента может явно учитывать дополнительную информацию о дисперсии выборок и их структуре. Необходимо исследовать, какой выигрыш даёт эта информация, сравнив мощности и средние достигаемые уровни значимости вариантов критериев при различных значениях параметров.
$H_0\,:\; \mathbb{E}(x)=\mathbb{E}(y), \;\; H_1\,:\; \mathbb{E}(x)\neq\mathbb{E}(y).$

Парный критерий Стьюдента и версия для независимых выборок и неизвестных неравных дисперсий.

$x^n,\;\; x \sim N(0,1), y^n = x^n + z^n, \;\; z\sim N(\mu,\sigma^2).$

Платонова Елена: $\sigma=1, \;\; \mu=-2\,:\,0.01\,:\,2, \;\; n=5\,:\,1\,:\,100.$

Семенов Олег: $\sigma=0.01\,:\,0.01\,:\,2, \;\; \mu=-2\,:\,0.01\,:\,2, \;\; n=100.$

Критерий Стьюдента для независимых выборок, версии для неизвестных и известных неравных дисперсий.

$x^n,\;\; x \sim N(0,1), y^n, \;\; y \sim N(\mu,\sigma^2).$

Сидоров Юрий: $\sigma=0.01\,:\,0.01\,:\,2, \;\; \mu=-2\,:\,0.01\,:\,2, \;\; n=50.$

Солодкин Дмитрий: $\sigma=0.01\,:\,0.01\,:\,2, \;\; \mu=0.5, \;\; n=5\,:\,1\,:\,100.$

Парный критерий Стьюдента и версия для независимых выборок и известных неравных дисперсий.

$x^n, \;\; x \sim N(0,1), y^n = x^n + z^n, \;\; z\sim N(\mu,\sigma^2)$
(cогласно свойствам нормального распределения, $var\left(y\right)=\sigma^2+1$ .)