Статистический анализ данных (курс лекций, К.В.Воронцов)/2012, ФУПМ

Материал из MachineLearning.

Версия от 17:47, 12 апреля 2012; Riabenko (Обсуждение | вклад)

(разн.) ← Предыдущая | Текущая версия (разн.) | Следующая → (разн.)

Содержание

1 Задание 1. Исследование свойств одномерных статистических критериев на модельных данных
- 1.1 Пример задания
- 1.2 Задания
  - 1.2.1 Анализ поведения разновидностей критерия Стьюдента
  - 1.2.2 Анализ поведения схожих критериев
2 Задание 2. Анализ реальных данных
3 Литература
4 Ссылки

Задание 1. Исследование свойств одномерных статистических критериев на модельных данных

Необходимо провести исследование одного или нескольких классических критериев проверки статистических гипотез. Интерес представляет поведение достигаемого уровня значимости (p-value) как функции размера выборок и параметров распределения. В соответствии с индивидуальными параметрами задания необходимо указанным способом сгенерировать одну или несколько выборок из заданного распределения, выполнить проверку гипотезы при помощи соответствующего критерия, а затем многократно повторить эту процедуру для различных значений параметров. По результатам расчётов необходимо построить требуемые в задании графики, среди которых могут быть следующие:

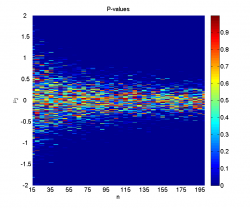
график зависимости достигаемого уровня значимости от значений параметров при однократном проведении эксперимента;
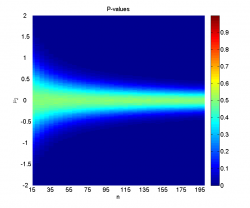
график зависимости достигаемого уровня значимости одного или двух критериев от значений параметров, усреднённого по большому количеству повторений эксперимента (например, по 1000 повторений);
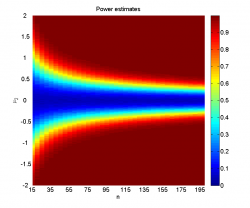
график с эмпирическими оценками мощности одного или двух критериев для разных значений параметров.

В качестве оценки мощности принимается доля отвержений нулевой гипотезы среди всех проверок. То есть, если эксперимент повторялся $k$ раз для каждого набора значений параметров, и в $m$ из $k$ случаев гипотеза была отвергнута на некотором фиксированном уровне значимости $\alpha$ (примем $\alpha=0.05$ ), оценкой мощности будет отношение $m/k.$

Необходимо сдать: выполненный в LaTex или Microsoft Word отчёт с описанием алгоритма, построенными графиками и выводами (объяснение полученных результатов моделирования, границы применимости критерия и т.д.), а также *.m-файл или R-скрипт, при запуске которого на экран выводятся графики, соответствующие имеющимся в отчёте.

Задание принимается до первого апреля.

Пример задания

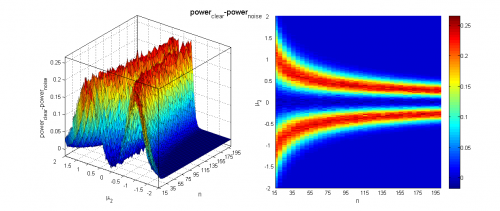
Исследуем чувствительность классического двухвыборочного критерия Стьюдента для проверки гипотезы однородности против альтернативы сдвига при зашумлении выборок наблюдениями, взятыми из равномерного распределения.

$x^n, \;\; x \sim 0.9\cdot N(\mu_1,1)+ 0.1\cdot U\left[-5+\mu_1,5+\mu_1\right]$ — выборка длины $n$ из смеси стандартного нормального $N(\mu_1,1)$ и равномерного $U\left[-5+\mu_1,5+\mu_1\right]$ распределений с весами $0.9$ и $0.1$ соответственно (при генерации выборки используется случайный датчик — если его значение не превосходит $0.9$ , то добавляем в выборку элемент, взятый из нормального распределения, иначе — элемент, взятый из равномерного).

$y^n, \;\; y \sim 0.9\cdot N(\mu_2,1)+ 0.1\cdot U\left[-5+\mu_2,5+\mu_2\right]$ — аналогичная выборка.

$H_0\,:\; \mathbb{E}(x)=\mathbb{E}(y), \;\; H_1\,:\; \mathbb{E}(x)\neq\mathbb{E}(y).$

$\mu_1=0, \;\; \mu_2=-2\,:\,0.01\,:\,2, \;\; n=15\,:\,5\,:\,200.$

При каждом значении $\mu_2$ выборки для разных значений $n$ генерируются независимо.

Значения достигаемого уровня значимости при однократной генерации выборок.

Значения достигаемого уровня значимости, усрёднённые по 3000 экспериментам.

Значения эмпирических оценок мощности критерия при проведении 3000 экспериментов $(\alpha=0.05).$

Заметим, что однократная генерация выборок даёт достаточно нестабильные результаты, не позволяя точно оценить границы области, где нулевая гипотеза отклоняется, поэтому и необходимо усреднение по большому числу экспериментов.

Видно, что при достаточно большой разнице между средними и большом размере выборок наличие шума не мешает уверенно отклонять гипотезу однородности. Когда, наоборот, разница между средними невелика (меньше 0.2-0.5 в зависимости от размера выборок), мощность близка к нулю, а среднее значение достигаемого уровня значимости колеблется около 0.5, что логично, так как его распределение при справедливости нулевой гипотезы равномерно на $[0,1]$ .

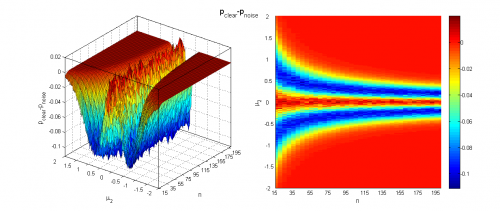
Чтобы оценить вклад зашумления выборок, оценим при всех значениях параметра мощность критерия и средний достигаемый уровень значимости на аналогичных выборках без шума и сравним результаты.

Разность средних достигаемых уровней значимости на выборках без шума и с шумом.

Разность эмпирических оценок мощности на выборках без шума и с шумом.

Видно, что наличие шума всё меньше влияет на работу критерия с ростом объёма выборок и разницы между их средними. Тем не менее, в некоторых областях изменения параметров потеря мощности из-за 10% зашумления может составлять до 20%, а средний достигаемый уровень значимости может быть выше на 0.1.

Отметим, что приведённые количественные выводы справедливы только для шума рассматриваемой структуры.

Задания

Анализ поведения разновидностей критерия Стьюдента

Критерий Стьюдента может явно учитывать дополнительную информацию о дисперсии выборок и их структуре. Необходимо исследовать, какой выигрыш даёт эта информация, сравнив мощности и средние достигаемые уровни значимости вариантов критериев при различных значениях параметров.
$H_0\,:\; \mathbb{E}(x)=\mathbb{E}(y), \;\; H_1\,:\; \mathbb{E}(x)\neq\mathbb{E}(y).$

Парный критерий Стьюдента и версия для независимых выборок и неизвестных неравных дисперсий.

$x^n,\;\; x \sim N(0,1), <br> y^n = x^n + z^n, \;\; z\sim N(\mu,\sigma^2).$

Токмакова Александра: $\sigma=1, \;\; \mu=-2\,:\,0.01\,:\,2, \;\; n=5\,:\,1\,:\,100.$

Габдрахманов Айдар: $\sigma=0.01\,:\,0.01\,:\,2, \;\; \mu=-1\,:\,0.005\,:\,1, \;\; n=100.$

Критерий Стьюдента для независимых выборок, версии для неизвестных и известных неравных дисперсий.

$x^n,\;\; x \sim N(0,1), <br> y^n, \;\; y \sim N(\mu,\sigma^2).$

Леонтьева Любовь: $\sigma=0.01\,:\,0.01\,:\,2, \;\; \mu=-2\,:\,0.01\,:\,2, \;\; n=50.$

Андрианов Павел: $\sigma=0.01\,:\,0.01\,:\,2, \;\; \mu=0.5, \;\; n=5\,:\,1\,:\,100.$

Парный критерий Стьюдента и версия для независимых выборок и известных неравных дисперсий.

$x^n, \;\; x \sim N(0,1), <br> y^n = x^n + z^n, \;\; z\sim N(\mu,\sigma^2)$
(cогласно свойствам нормального распределения, $var\left(y\right)=\sigma^2+1$ .)

Краснова Ксения: $\sigma=1, \;\; \mu=-2\,:\,0.01\,:\,2, \;\; n=5\,:\,1\,:\,100.$

Бузун Назар : $\sigma=0.01\,:\,0.01\,:\,2, \;\; \mu=-1\,:\,0.005\,:\,1, \;\; n=100.$

Анализ поведения схожих критериев

Требуется исследовать поведение указанной пары статистических критериев, подходящих для решения одной и той же задачи, сравнить мощность и достигаемые уровни значимости и сделать выводы о границах применимости критериев. Необходимо для каждого из критериев построить графики зависимости достигаемых уровней значимости и оценок мощностей от параметров, и показать, в каких областях изменения параметров предпочтительнее использовать тот или иной критерий.

$x^n, \;\; x \sim Ber(p);$
$H_0\,:\; p\leq p_0, \;\;\; H_1\,:\; p>p_0.$

Ибрагимов Рустам: точный биномиальный критерий и z-критерий, $p_0=0.5, \;\; p=0 \,:\, 0.01 \,:\, 1, \;\; n=10\,:\,5\,:\,100.$

Кокшаров Михаил: точный биномиальный критерий и z-критерий, $p_0=0.75, \;\; p=0 \,:\, 0.01 \,:\, 1, \;\; n=10\,:\,5\,:\,100.$

Оленин Алексей: точный биномиальный критерий и z-критерий, $p_0=0 \,:\, 0.01 \,:\, 1, \;\; p=0 \,:\, 0.01 \,:\, 1, \;\; n=50.$

$x^n, \;\; x \sim N(0,1), \;\; y^n = x^n + z^n, \;\; z\sim N(\mu,\sigma^2);$
$H_0\,:$ средние двух выборок равны, $\;H_1\,:$ средние двух выборок не равны;

Илья Козлов: критерий Стьюдента для связных выборок и критерий Уилкоксона, $n=50, \;\; \mu=-2\,:\,0.02\,:\,2,\;\; \sigma=0.1\,:\,0.05\,:\,5.$

Гребенников Евгений: критерий Стьюдента для связных выборок и критерий Уилкоксона, $n=10\,:\,5\,:\,100, \;\; \mu=-2\,:\,0.02\,:\,2,\;\; \sigma=2.$

Будников Егор: критерий Стьюдента для связных выборок и перестановочный критерий, $n=10\,:\,5\,:\,100, \;\; \mu=-2\,:\,0.02\,:\,2,\;\; \sigma=2.$

$x^n, \;\; x \sim N(0,1),\;\;y^n, \;\; y \sim N(\mu,1);$
$H_0\,:$ средние двух выборок равны, $\;H_1\,:$ средние двух выборок не равны;
$\mu=-2\,:\,0.02\,:\,2;\;\; n=10\,:\,5\,:\,100.$

Савченко Валерий: двухвыборочный критерий Стьюдента для независимых выборок и критерий Уилкоксона-Манна-Уитни.

Захаров Илья: критерий Уилкоксона-Манна-Уитни и медианный критерий.

Рудой Георгий: критерий Уилкоксона-Манна-Уитни и двухвыборочный перестановочный критерий.

$x^n, \;\; x \sim p\cdot N(0,1)+ \left(1-p\right)\cdot U\left[-a,a\right]$ — выборка длины $n$ из смеси стандартного нормального $N(0,1)$ и равномерного $U\left[-a,a\right]$ распределений с весами $p$ и $1-p$ соответственно (при генерации выборки используется случайный датчик — если его значение не превосходит $p$ , то добавляем в выборку элемент, взятый из нормального распределения, иначе — элемент, взятый из равномерного).
$H_0\,:\; x \sim N(0,1), \;\;\; H_1\,:\; H_0$ неверна;
$p=0\,:\,0.02\,:\,1; \;\; n=10\,:\,5\,:\,100.$

Гафиатуллина Ильнара: критерий Шапиро-Уилка и критерий Колмогорова-Смирнова, $a=1.$

Романенко Александр: критерий омега-квадрат и критерий Шапиро-Уилка, $a=2.$

Хаспулатова Юлия: критерий хи-квадрат и критерий омега-квадрат, $a=5.$

Ямщиков Илья: критерий Колмогорова-Смирнова и критерий хи-квадрат, $a=7.$

$x^n, \;\; x \sim N(\mu,1);$
$H_0\,:$ среднее выборки равно нулю, $\;H_1\,:$ среднее выборки не равно нулю;
$\mu=-2\,:\,0.01\,:\,2,\;\; n=10\,:\,5\,:\,100.$

Аванесов Валерий: критерий знаков и критерий знаковых рангов Уилкоксона.

Мотренко Анастасия: критерий знаков и одновыборочный критерий Стьюдента.

Бурмистров Михаил: критерий знаковых рангов Уилкоксона и одновыборочный перестановочный критерий.

Сергей Сергеев: одновыборочный критерий Стьюдента и одновыборочный перестановочный критерий.

Задание 2. Анализ реальных данных

Ниже приведены описания анализируемых данных и постановки задач. Сами данные каждый студент может получить по электронной почте после сдачи первого задания. При проведении анализа можно пользоваться любыми доступными программными средствами. Необходимо предоставить подробный письменный отчёт по проведённому исследованию, содержащий выводы и описания каждого этапа анализа — используемые методы, обоснование их применимости, промежуточные результаты вычислений, графики. Помимо выводов, касающихся математических особенностей решения, необходимо включить в отчёт заключения, сформулированные в терминах предметной области, которые могли бы быть понятны гипотетическому заказчику-нематематику.

Задание необходимо сдать до двадцать седьмого мая.

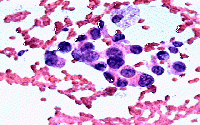
Клетки опухолей груди

Гистохимия пунктата злокачественной опухоли.

357 испытуемым с доброкачественными и 212 со злокачественными опухолями груди была сделана тонкоигольная аспирационная пункция с гистологическим исследованием пунктата. По полученным изображениям определялись следующие признаки опухолевых клеток: радиус, однородность текстуры, периметр, площадь, гладкость, компактность, степень вогнутости, доля вогнутых участков контура, симметричность, фрактальная размерность. Для каждого изображения были рассчитаны среднее значение каждого из этих признаков, стандартное отклонение и среднее по трём клеткам с максимальным значением признака.

Кокшаров Михаил: оценить вероятность того, что опухоль злокачественная, по набору рассчитанных по изображению признаков. Построить функции, дающие точечную оценку и границы 95% доверительного интервала.

Массовая доля жира в организме

Массовая доля жира, важная характеристика здоровья, рассчитывается через плотность тела, измеряемую при помощи взвешивания в воде. Для 252 мужчин проведены такие расчёты. Имеются также данные антропометрии (возраст, рост, вес, обхват грудной клетки и т.д.)

Гребенников Евгений: построить функцию, оценивающую массовую долю жира по легко измеряемым антропометрическим признакам.

Краснова Ксения: построить функцию, оценивающую индекс ожирения без использования данных взвешивания.

Посещаемость сервиса "Яндекс.Открытки"

Измерена месячная аудитория сервиса "Яндекс.Открытки" с мая 2008 по февраль 2012 г.

Романенко Александр: предсказать месячную аудиторию на период с марта 2012 по февраль 2013 г.

Краш-тест с манекенами

Имеются результаты 352 краш-тестов, при которых происходило лобовое столкновение автомобилей с бетонной стеной на скорости около 60 км/ч. Измерены показатели повреждения манекенов: критерий тяжести повреждений головы, замедление грудной клетки, нагрузка на левое и правое бедро.

Леонтьева Любовь: исследовать зависимость показателей повреждения от типа кузова, вида средств защиты, места манекена, веса автомобиля.

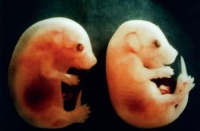
Генетически модифицированные мыши с синдромом Дауна

Эмбрионы мышей с внедрённой копией участка 21-й хромосомы человека (слева) и без (справа).

Синдром Дауна — геномная патология, характеризующаяся наличием дополнительной копии генетического материала по 21-й хромосоме. В целях исследования болезни Дауна была создана популяция мышей с внедрённой копией одного из участков 21-й хромосомы человека. Первому поколению мышей внедрялся один из четырёх участков, затем они скрещивались с немодифицированными мышами, и внедрённый учасок мог передаваться потомкам. Все они оказались слепыми, поэтому невозможно было провести прямую проверку уровня их интеллекта. Для 500 особей известны: наименование внедрённого участка хромосомы (A=141G6; B=152F7; C=230E8; D=285E6), номер линии мышей (мыши, произошедшие от одной и той же трансгенной особи, относятся к одной линии), пол особи, вес, возраст, в котором он был измерен, номер клетки, в которой жила особь, а также индикатор содержания в её ДНК человеческого материала.

Будников Егор: люди, страдающие болезнью Дауна, более склонны к ожирению; справедливо ли это для генетически модифицированных мышей? Исследовать различия с учётом всех остальных факторов.

Электрическая прочность диэлектрика

Была измерена электрическая прочность изоляции проводов на разных сроках их эксплуатации и при различной температуре. Известно, что зависимость электрической прочности диэлектрика от времени и температуры имеет вид $\log(y)=\beta_1-\beta_2\cdot time \cdot e^{-\beta_3\cdot temperature}+\epsilon$ .

Бурмистров Михаил: найти значения констант $\beta_1, \beta_2, \beta_3,$ построить для них доверительные области, оценить качество построенной модели.

Ценообразование бриллиантов

Имеются данные о цене и потребительских качествах 308 бриллиантов, продававшихся в Сингапуре в 2000 году. Известны: вес бриллианта в каратах, цвет (закодирован буквами латинского алфавита: наиболее чистый цвет — буквой D, менее чистые — буквами E, F, G и т.д., чем ближе к концу алфавита, тем "грязнее"), группа чистоты (отсутствие дефектов, профессиональная оценка, выдаваемая специалистами при исследовании бриллианта в лупу десятикратного увеличения; бриллианты без трещин и включений получают оценку IF ("internally flawless"), далее в порядке убывания чистоты следуют группы VVS1 и VVS2 ("very very slightly imperfect"), VS1 и VS2 ("very slightly imperfect")), название организации, выдавшей сертификат по группе чистоты (GIA — Gemmological Institute of America, IGI — International Gemmological Institute, HRD — Hoge Raad Voor Diamant), стоимость бриллианта в сингапурских долларах.

Токмакова Александра: построить модель ценообразования бриллиантов, учитывая все особенности имеющихся данных.

Захаров Илья: существует общепринятая система классификации бриллиантов на мелкие — до 0.29 карата, средние — от 0.30 до 0.99 карата и крупные — свыше 1 карата. Достаточно ли для предсказания цены знать о весе бриллианта только к какому классу он относится, или предсказания с использованием знаний о точном весе значимо лучше?

Линька metacarcinus magister

Metacarcinus magister.

У 472 самок metacarcinus magister измерена ширина панциря до и после линьки. Часть особей проживала в лаборатории, часть — в естественной среде обитания; для последних известен также год вылова.

Ямщиков Илья: построить модель изменения размеров панциря с учётом всех факторов.

Андрианов Павел: исследовать различия между изменениями размеров панциря особей, линька которых проходила в лабораторных условиях и в естественных; для последних оценить влияние года вылова.

Солнечная активность

В центре исследования солнечной активности Цюрихской обсерватории собраны данные о среднем числе солнечных пятен за каждый месяц с января 1749 года.

Аванесов Валерий: предсказать среднее число солнечных пятен на каждый месяц до конца 2020 года.

Оптимальные условия размножения штаммов золотистого стафилококка

При подозрении на инфекционное заболевание для правильной постановки диагноза часто бывает важно из взятых у пациентов образцов вырастить как можно более многочисленную колонию бактерий, чтобы её было удобнее исследовать. Считается, что оптимальные параметры для размножения штаммов стафилококка в лабораторных условиях следующие: температура 35 градусов, концентрация триптона в питательном растворе 1.0%, время выдержки 24 часа. Для проверки оптимальности этих условий было проведено 30 экспериментов над пятью различными штаммами стафилококка. Для каждого из экспериментов известны время выдержки, температура, концентрация триптона, а также измеренное по окончании выдержки число колониеобразующих единиц (КОЕ) бактерий каждого штамма.

Хаспулатова Юлия: построить функцию, предсказывающую итоговое суммарное число КОЕ бактерий всех пяти штаммов по времени выдержки, температуре и концентрации триптона в растворе, и определить по ней оптимальные условия размножения стафилококка.

Бузун Назар: одинакова ли зависимость итогового числа КОЕ разных штаммов стафилококка от внешних условий?

Диагностика заболеваний позвоночника

Для 310 испытуемых измерены: наклон и смещение таза, угол изгиба поясницы, наклон плоскости тазовой поверхности крестца, радиус таза, степень смещения позвонков. Каждый из испытуемых либо здоров, либо болен спондилолистезом или межпозвонковой грыжей.

Мотренко Анастасия: построить функцию, предсказывающую вероятность наличия заболевания позвоночника, и доверительный интервал для неё.

Габдрахманов Айдар: построить функцию, предсказывающую вероятность наличия каждого из рассматриваемых заболеваний позвоночника, и доверительные интервалы для них.

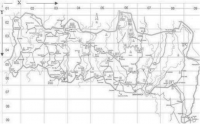
Лесные пожары в парке Монтезинью

Парк Монтезинью, разбиение на зоны.

Данные собраны в 2001-2003 годах в португальском природном парке Монтезинью. Известны: месяц и день недели, температура воздуха, относительная влажность, скорость ветра, число выпавших осадков, значения четырёх метеорологических индексов, координаты зоны, в которой были произведены эти измерения (см. рис.), а также площадь леса, уничтоженного произошедшим в этот день пожаром (если он был).

Савченко Валерий: построить модель, позволяющую оценить по рассматриваемым признакам вероятность пожара и доверительный интервал для неё.

Гафиатуллина Ильнара: построить модель, предсказывающую площадь леса, уничтоженного пожаром.

Оленин Алексей: известно, что метеорологические индексы каким-то образом рассчитываются на основе приведённых простых метеорологических показателей (температуры, влажности и т.д.). Построить и сравнить модели, предсказывающие площадь леса, уничтоженного пожаром, по двум наборам признаков: в один не входят простые метеороголические показатели, а из другого исключены метеорологические индексы.

Литература

Кобзарь А. И. Прикладная математическая статистика. — М.: Физматлит, 2006.

Ссылки

Источник — «http://machinelearning.ru/wiki/index.php?title=%D0%A1%D1%82%D0%B0%D1%82%D0%B8%D1%81%D1%82%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D0%B9_%D0%B0%D0%BD%D0%B0%D0%BB%D0%B8%D0%B7_%D0%B4%D0%B0%D0%BD%D0%BD%D1%8B%D1%85_%28%D0%BA%D1%83%D1%80%D1%81_%D0%BB%D0%B5%D0%BA%D1%86%D0%B8%D0%B9%2C_%D0%9A.%D0%92.%D0%92%D0%BE%D1%80%D0%BE%D0%BD%D1%86%D0%BE%D0%B2%29/2012%2C_%D0%A4%D0%A3%D0%9F%D0%9C»

Категория: Учебные курсы