Материал из MachineLearning.

| Формулировка задания находится в стадии формирования. Просьба не приступать к выполнению задания до тех пор, пока это предупреждение не будет удалено.
|
-
Начало выполнения задания: 27 сентября 2012
Срок сдачи: 10 октября 2012, 23:59
Среда реализации задания – MATLAB. Неэффективная реализация кода может негативно отразиться на оценке.
Формулировка задания
Рассматривается линейная динамическая система (ЛДС), в которой полное правдоподобие задается как:
=p(t_1)\prod_{n=2}^Np(t_n |t_{n-1})\prod_{n=1}^Np(x_n |t_n ),\\
p(t_n|t_{n-1})=\mathcal{N}(t_n|At_{n-1},\Gamma),\\
p(x_n|t_n)=\mathcal{N}(x_n|Ct_n,\Sigma),\\
p(t_1)=\mathcal{N}(t_1|\mu_0,V_0).
)
Все переменные модели являются непрерывными, т.е. 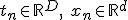 . Параметры модели
. Параметры модели 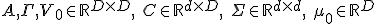 .
.
Данную ЛДС нужно протестировать на модельной задаче сопровождения (трекинга) объекта в пространстве.
Рассматривается также нелинейная динамическая система с нормальным шумом, в которой вероятности переходов задаются как:
 = \mathcal{N}(t_n|f(t_{n-1}),\Gamma),\\
p(x_n|t_n) = \mathcal{N}(x_n|g(t_n),\Sigma),\\
p(t_1) = \mathcal{N}(t_1|\mu_0,V_0).
)
Здесь 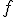 и
и 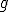 — известные вектор-функции.
— известные вектор-функции.
Для этой системы нужно реализовать расширенный фильтр Калмана и протестировать его работу на модельных данных.
Для выполнения задания необходимо:
- Реализовать алгоритм генерации выборки из вероятностной модели ЛДС и нелинейной ДС;
- Реализовать алгоритм онлайн фильтрации сигнала с помощью фильтра Калмана и с помощью расширенного фильтра Калмана;
- Реализовать обучение параметров ЛДС с учителем. При этом часть параметров ЛДС может быть задана пользователем;
- Протестировать реализованные алгоритмы на модельных данных;
- Написать отчет в формате PDF с описанием всех проведенных исследований. Данный отчет должен, в частности, включать в себя графики фильтрации сгенерированных траекторий для линейного и нелинейного случая.
Спецификация реализуемых функций
| Генерация выборки для ЛДС
|
| [X, T] = LDS_generate(N, A, C, G, S, mu0, V0)
|
| ВХОД
|
| N — количество точек в генерируемой последовательности, uint32;
|
A — матрица преобразования среднего в последовательности 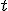 , матрица типа double размера D x D; , матрица типа double размера D x D;
|
C — матрица преобразования среднего при переходе от 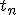 к к 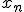 , матрица типа double размера d x D; , матрица типа double размера d x D;
|
G — ковариационная матрица для распределения ) , матрица типа double размера D x D; , матрица типа double размера D x D;
|
S — ковариационная матрица для распределения ) , матрица типа double размера d x d; , матрица типа double размера d x d;
|
mu0 — мат.ожидание априорного распределения ) , матрица типа double размера 1 x D; , матрица типа double размера 1 x D;
|
V0 — ковариационная матрица априорного распределения ) , матрица типа double размера D x D. , матрица типа double размера D x D.
|
|
| ВЫХОД
|
| X — сгенерированная наблюдаемая последовательность, матрица типа double размера N x d
|
| T — последовательность скрытых характеристик, матрица типа double размера N x D
|
|
Обратите внимание: в процедуре LDS_generate параметры D и d определяются неявно по размеру соответствующих элементов.
| Фильтр Калмана для ЛДС
|
| [M, V] = LDS_filter(X, A, C, G, S, mu0, V0)
|
| ВХОД
|
| X — входная последовательность, матрица типа double размера N x d, где N – количество точек в последовательности, d – количество признаков;
|
A — матрица преобразования среднего в последовательности 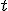 , матрица типа double размера D x D; , матрица типа double размера D x D;
|
C — матрица преобразования среднего при переходе от 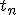 к к 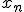 , матрица типа double размера d x D; , матрица типа double размера d x D;
|
G — ковариационная матрица для распределения ) , матрица типа double размера D x D; , матрица типа double размера D x D;
|
S — ковариационная матрица для распределения ) , матрица типа double размера d x d; , матрица типа double размера d x d;
|
mu0 — мат.ожидание априорного распределения ) , матрица типа double размера 1 x D; , матрица типа double размера 1 x D;
|
V0 — ковариационная матрица априорного распределения ) , матрица типа double размера D x D. , матрица типа double размера D x D.
|
|
| ВЫХОД
|
M — мат. ожидания распределений ) , матрица типа double размера N x D; , матрица типа double размера N x D;
|
V — ковариационные матрицы распределений ) , массив типа double размера D x D x N; , массив типа double размера D x D x N;
|
|
| Обучение с учителем для ЛДС
|
| [A, C, G, S] = LDS_train(X, T, ParameterName1, ParameterValue1, ParameterName2, ParameterValue2, ...)
|
| ВХОД
|
| X — входная последовательность наблюдаемых переменных, матрица типа double размера N x d, где N – количество точек в последовательности, d – число признаков;
|
| T — входная последовательность значений скрытых характеристик, матрица типа double размера N x D;
|
| (ParameterName, ParameterValue) — (необязательные аргументы) набор дополнительных параметров, возможны следующие названия параметров:
|
'A' — задаваемая пользователем матрица преобразования среднего в распределении ) (соответственно, ее не нужно вычислять внутри функции); (соответственно, ее не нужно вычислять внутри функции);
|
'C' — задаваемая пользователем матрица преобразования среднего в распределении ) ; ;
|
'G' — задаваемая пользователем матрица ковариации ) ; ;
|
'S' — задаваемая пользователем матрица ковариации в распределении ) ; ;
|
|
| ВЫХОД
|
A — матрица преобразования среднего в последовательности 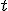 , матрица типа double размера D x D; , матрица типа double размера D x D;
|
C — матрица преобразования среднего при переходе от 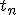 к к 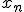 , матрица типа double размера d x D; , матрица типа double размера d x D;
|
G — ковариационная матрица для распределения ) , матрица типа double размера D x D; , матрица типа double размера D x D;
|
S — ковариационная матрица для распределения ) , матрица типа double размера d x d; , матрица типа double размера d x d;
|
|
| Генерация выборки для нелинейной динамической системы
|
| [X, T] = EKF_generate(N, func_horiz, func_vert, G, S, mu0, V0)
|
| ВХОД
|
| N — количество точек в генерируемой последовательности, uint32;
|
func_horiz — указатель на функцию 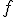 , сама функция должна возвращать две величины: значение (вектор длины D) и градиент (матрицу размера D x D); , сама функция должна возвращать две величины: значение (вектор длины D) и градиент (матрицу размера D x D);
|
func_vert — указатель на функцию 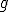 , сама функция должна возвращать свое значение (вектор длины d) и градиент (матрицу размера d x D); , сама функция должна возвращать свое значение (вектор длины d) и градиент (матрицу размера d x D);
|
G — ковариационная матрица для распределения ) , матрица типа double размера D x D; , матрица типа double размера D x D;
|
S — ковариационная матрица для распределения ) , матрица типа double размера d x d; , матрица типа double размера d x d;
|
mu0 — мат.ожидание априорного распределения ) , матрица типа double размера 1 x D; , матрица типа double размера 1 x D;
|
V0 — ковариационная матрица априорного распределения ) , матрица типа double размера D x D. , матрица типа double размера D x D.
|
|
| ВЫХОД
|
| X — сгенерированная наблюдаемая последовательность, матрица типа double размера N x d
|
| T — последовательность скрытых характеристик, матрица типа double размера N x D
|
|
Обратите внимание: в процедуре EKF_generate параметры D и d определяются неявно по размеру соответствующих элементов.
| Расширенный фильтр Калмана для нелинейной динамической системы
|
| [M, V] = EKF_filter(X, func_horiz, func_vert, G, S, mu0, V0)
|
| ВХОД
|
| X — входная последовательность, матрица типа double размера N x d, где N – количество точек в последовательности, d – количество признаков;
|
func_horiz — указатель на функцию 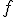 , сама функция должна возвращать две величины: значение (вектор длины D) и градиент (матрицу размера D x D); , сама функция должна возвращать две величины: значение (вектор длины D) и градиент (матрицу размера D x D);
|
func_vert — указатель на функцию 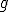 , сама функция должна возвращать свое значение (вектор длины d) и градиент (матрицу размера d x D); , сама функция должна возвращать свое значение (вектор длины d) и градиент (матрицу размера d x D);
|
G — ковариационная матрица для распределения ) , матрица типа double размера D x D; , матрица типа double размера D x D;
|
S — ковариационная матрица для распределения ) , матрица типа double размера d x d; , матрица типа double размера d x d;
|
mu0 — мат.ожидание априорного распределения ) , матрица типа double размера 1 x D; , матрица типа double размера 1 x D;
|
V0 — ковариационная матрица априорного распределения ) , матрица типа double размера D x D. , матрица типа double размера D x D.
|
|
| ВЫХОД
|
M — мат. ожидания распределений ) , матрица типа double размера N x D; , матрица типа double размера N x D;
|
V — ковариационные матрицы распределений ) , массив типа double размера D x D x N; , массив типа double размера D x D x N;
|
|
Рекомендации по выполнению задания
- В качестве модельных данных для тестирования ЛДС рассмотреть задачу сопровождения объекта в двухмерном пространстве. Для генерации траектории движения объекта использовать функцию LDS_generate с параметрами, описанными в лекции. При этом рекомендуется взять небольшой квант времени
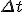 . Убедиться в том, что отфильтрованная по Калману траектория ближе к истинной, чем наблюдаемый сигнал.
. Убедиться в том, что отфильтрованная по Калману траектория ближе к истинной, чем наблюдаемый сигнал.
- При тестировании обучения с учителем убедиться в том, что правдоподобие траектории объекта в двухмерном пространстве, сгенерированной с помощью LDS_generate, не превосходит правдоподобие этой траектории для параметров, полученных с помощью LDS_train.
Оформление задания
Выполненный вариант задания необходимо прислать письмом по адресу bayesml@gmail.com с темой «[МОМО12] Задание 1. ФИО». Убедительная просьба присылать выполненное задание только один раз с окончательным вариантом. Новые версии будут рассматриваться только в самом крайнем случае. Также убедительная просьба строго придерживаться заданной выше спецификации реализуемых функций. Очень трудно проверять большое количество заданий, если у каждого будет свой формат реализации.
Письмо должно содержать:
- PDF-файл с описанием проведенных исследований
- Набор вспомогательных файлов при необходимости
. Параметры модели
.
и
— известные вектор-функции.
. Убедиться в том, что отфильтрованная по Калману траектория ближе к истинной, чем наблюдаемый сигнал.


