Методы оптимизации в машинном обучении (курс лекций)/2012/Задание 2

Материал из MachineLearning.

Внимание! Текст задания находится в стадии формирования. Просьба не приступать к выполнению задания до тех пор, пока это предупреждение не будет удалено.

Основная статья: Методы оптимизации в машинном обучении (курс лекций)

Начало выполнения задания: 27 октября 2012

Срок сдачи: 9 ноября (пятница), 23:59

Среда реализации задания – MATLAB.

Логистическая регрессия

Формулировка метода

Рассматривается задача классификации на два класса. Имеется обучающая выборка , где — вектор признаков для объекта , а — его метка класса. Задача заключается в предсказании метки класса для объекта, представленного своим вектором признаков .

В логистической регрессии предсказание метки класса осуществляется по знаку линейной функции:

,

где — некоторые веса. Настройка весов осуществляется путем минимизации следующего регуляризованного критерия:

.

Здесь — задаваемый пользователем параметр регуляризации.

Использование базисных функций

Использование 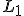-регуляризации

Формулировка задания

• Реализовать процедуру обучения логистической регрессии с квадратичной регуляризацией с помощью трех подходов:
  1. Метод Ньютона с ограниченным шагом (damped Newton) и адаптивным подбором длины шага,
  2. Метод L-BFGS с подбором длины шага через backtracking,
  3. Метод на основе верхней оценки Йакколы-Джордана для логистической функции, в котором на этапе решения СЛАУ используется метод сопряженных градиентов;
• Провести тестирование разработанных методов на модельных данных для различных сочетаний количества объектов и признаков, особое внимание при этом необходимо уделить случаю данных большого объема;
• Реализовать процедуру обучения -регуляризованной логистической регрессии с помощью двух подходов:
  1. Метод покоординатного спуска с подбором длины шага через backtracking,
  2. Метод с использованием верхней оценки Йаккола-Джордана для логистической функции и квадратичной оценки для функции модуля, в котором на этапе решения СЛАУ используется метод сопряженных градиентов;
• Провести тестирование разработанных методов на модельных данных для различных сочетаний количества объектов и признаков, особое внимание при этом необходимо уделить ситуации, когда число признаков превосходит число объектов, и случаю данных большого объема;
• Написать отчет в формате PDF с описанием всех проведенных исследований. Данный отчет должен содержать, в частности, необходимые формулы для методов с использованием верхних оценок: вид оптимизируемого функционала и формулы пересчета параметров.

Спецификация реализуемых функций

Минимизация функции с помощью метода Ньютона с ограниченным шагом
[x, f] = min_dampednewton(func, x0, param_name1, param_value1, ...)
ВХОД
func — указатель на минимизируемую функцию; x0 — начальное приближение, вектор; (param_name, param_value) — необязательные параметры, следующие названия и значения возможны: 'eps' — точность оптимизации по функции и аргументу, число, по умолчанию = 1e-5; 'params' — параметры процедуры адаптивной коррекции длины шага, вектор из двух чисел [alpha, v], где alpha — начальное значение длины шага, а v — мультипликатор шага; 'max_iter' — максимальное число итераций, число, по умолчанию = 100; 'display' — режим отображения, true или false, если true, то отображаются номер итерации, текущее значение функции, норма разности между аргументами на последней и предпоследней итерациях и др. показатели, по умолчанию = false;
ВЫХОД
x — найденное значение аргумента, вектор длины D; f — значение функции в точке оптимума x, число.

Прототип функции min_lbfgs для минимизации функции с помощью метода L-BFGS выглядит аналогично, 'params' определяет параметры метода backtracking для поиска оптимальной длины шага на очередной итерации. Возможным значением 'params' является вектор из трех чисел [alpha beta rho], где alpha — начальная длина шага, beta — делитель шага, rho — параметр из первого условия Флетчера.

Обучение логистической регрессии с помощью верхних оценок
[w, f] = logreg_ub(X, t, lambda, w0, param_name1, param_value1, ...)
ВХОД
X — обучающая выборка, матрица размера N x D, где N — число объектов, D — число признаков; t — метки классов для обучающей выборки, вектор длины N со значениями +1 и -1; lambda — значение параметра регуляризации, число; w0 — начальный вектор весов, вектор длины D; (param_name, param_value) — необязательные параметры, следующие названия и значения возможны: 'regul' — вид регуляризации, строка, возможные значения 'L2' и 'L1', по умолчанию = 'L2'; 'LS' — стратегия для решения промежуточных СЛАУ, строка, по умолчанию = 'chol', возможные значения: 'chol' — разложение Холецкого, эквивалентно матлабовской операции A\b; 'cg-full' — метод сопряженных градиентов, в котором операция умножения матрицы A на вектор w выполняется непосредственно; 'cg-cons' — метод сопряженных градиентов, в котором операция вида реализуется как . 'eps' — точность оптимизации по функции и аргументу, число, по умолчанию = 1e-5; 'max_iter' — максимальное число итераций, число, по умолчанию = 100; 'display' — режим отображения, true или false, если true, то отображаются номер итерации, текущее значение верхней границы, норма разности между весами на последней и предпоследней итерациях и др. показатели, по умолчанию = false;
ВЫХОД
w — найденное значение весов, вектор длины D; f — значение верхней границы (совпадает с самой функцией) в точке оптимума w, число.

Обратите внимание, что точность решения СЛАУ при использовании метода сопряженных градиентов должна превышать заданную точность eps.

Оформление задания

Выполненный вариант задания необходимо прислать письмом по адресу bayesml@gmail.com с темой «[МОМО12] Задание 2. ФИО». Убедительная просьба присылать выполненное задание только один раз с окончательным вариантом. Новые версии будут рассматриваться только в самом крайнем случае. Также убедительная просьба строго придерживаться заданной выше спецификации реализуемых функций.

Письмо должно содержать:

• PDF-файл с описанием проведенных исследований;
• Файлы min_golden.m, min_quadratic.m, min_cubic.m, min_brent.m, min_fletcher.m;
• Набор вспомогательных файлов при необходимости.