Методы оптимизации в машинном обучении (курс лекций)/2012/Задание 3

Материал из MachineLearning.

Текст задания находится в стадии формирования. Просьба не приступать к выполнению задания до тех пор, пока это предупреждение не будет удалено.

Основная статья: Методы оптимизации в машинном обучении (курс лекций)

Начало выполнения задания: 24 ноября 2012

Срок сдачи: 7 декабря 2012 (пятница), 23:59

Среда реализации задания – MATLAB.

Модель 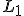-регуляризованной линейной регрессии

Формулировка задания

• Вывести двойственную задачу оптимизации для задачи обучения -регуляризованной линейной регрессии;
• Для полученной двойственной задачи предложить формулу вычисления допустимой двойственной точки по заданной прямой точке, на ее основе записать верхнюю оценку на зазор между решениями прямой и двойственной задач;
• Вывести необходимые формулы для решения гладкой задачи обучения (*) с помощью метода барьерных функций; предложить свой способ эффективного решения соответствующей СЛАУ, необходимые для этого формулы вставить в отчет;
• Реализовать метод барьерных функций для решения задачи (*);
• Вывести необходимые формулы для решения двойственной задачи с помощью прямо-двойственного метода внутренней точки; предложить свой способ эффективного решения возмущенной ККТ-системы, необходимые для этого формулы вставить в отчет;
• Реализовать прямо-двойственный метод внутренней точки для двойственной задачи;
• Реализовать на выбор проксимальный или покоординатный метод для решения задачи обучения -регуляризованной линейной регрессии;
• Провести экспериментальное сравнение трех реализованных методов на предмет скорости работы при 1) различных соотношениях между количеством объектов и признаков в данных и 2) различных значениях параметра точности ;
• Написать отчет в формате PDF с описанием всех проведенных исследований. Данный отчет должен содержать, в частности, необходимые формулы для всех методов. Также во всех приведенных экспериментах должно быть указано количество итераций, точность, параметры и время работы методов.

Спецификация реализуемых функций

Метод золотого сечения
[x_min, f_min, status] = min_golden(func, interval, param_name1, param_value1, ...)
ВХОД
func — указатель на оптимизируемую функцию; interval — границы интервала оптимизации, вектор типа double длины 2; (param_name, param_value) — необязательные параметры, следующие названия и значения возможны: 'eps' — точность оптимизации по аргументу, число, по умолчанию = 1e-5; 'max_iter' — максимальное число итераций, число, по умолчанию = 500; 'display' — режим отображения, true или false, если true, то отображаются номер итерации, текущее значение функции, аргумента, текущая точность и др. показатели, по умолчанию = false;
ВЫХОД
x_min — найденное значение минимума, число; f_min — значение функции в точке минимума, число; status — результаты оптимизации, структура со следующими полями: 'flag' — общий результат, число, равно 1, если достигнут оптимум с точностью eps, равно -1, если произошел выход по максимальному числу итераций; 'num_oracle' — количество обращений к оракулу;

Прототипы функций min_parabolic для метода парабол, min_qubic для кубических аппроксимаций и min_brent для метода Брента выглядят аналогично. В методе Брента добавляется параметр 'use_gradient' с возможными значениями true и false для учета случая оптимизации с производной и без. При отображении в методе Брента необходимо указывать способ выбора очередной точки на каждой итерации (golden/parabolic или bisection/parabolic).

Метод Флетчера
[alpha_min, f_min, status] = min_fletcher(func, x, d, param_name1, param_value1, ...)
ВХОД
func — указатель на оптимизируемую функцию; x — текущая точка, вектор типа double; d — направление минимизации, вектор типа double; (param_name, param_value) — необязательные параметры, следующие названия и значения возможны: 'params' — параметры метода [rho sigma tau xi], по умолчанию = [0.1 0.7 0.1 9]; 'max_iter' — максимальное число итераций, число, по умолчанию = 100; 'display' — режим отображения, true или false, по умолчанию = false;
ВЫХОД
alpha_min — найденное значение минимума для alpha, число; f_min — значение функции в точке минимума, число; status — результаты оптимизации, структура со следующими полями: 'flag' — общий результат, число, равно 1, если достигнут неточный оптимум, равно -1, если произошел выход по максимальному числу итераций; 'num_oracle' — количество обращений к оракулу;

Оформление задания

Выполненный вариант задания необходимо прислать письмом по адресу bayesml@gmail.com с темой «[МОМО12] Задание 3. ФИО». Убедительная просьба присылать выполненное задание только один раз с окончательным вариантом. Новые версии будут рассматриваться только в самом крайнем случае. Также убедительная просьба строго придерживаться заданной выше спецификации реализуемых функций.

Письмо должно содержать:

• PDF-файл с описанием проведенных исследований;
• Файлы min_golden.m, min_quadratic.m, min_cubic.m, min_brent.m, min_fletcher.m;
• Набор вспомогательных файлов при необходимости.