Применение метода главных компонент
Материал из MachineLearning.
Метод главных компонент - наиболее популярный метод сокращения размерности во многих приложениях.
Содержание |
Визуализация данных
Визуализация данных – представление в наглядной форме данных эксперимента или результатов теоретического исследования.
Первым выбором в визуализации множества данных является ортогональное проецирование на плоскость первых двух главных компонент (или 3-мерное пространство первых трёх главных компонент). Плоскость проектирования является, по сути плоским двумерным «экраном», расположенным таким образом, чтобы обеспечить «картинку» данных с наименьшими искажениями. Такая проекция будет оптимальна (среди всех ортогональных проекций на разные двумерные экраны) в трех отношениях:
- Минимальна сумма квадратов расстояний от точек данных до проекций на плоскость первых главных компонент, то есть экран расположен максимально близко по отношению к облаку точек.
- Минимальна сумма искажений квадратов расстояний между всеми парами точек из облака данных после проецирования точек на плоскость.
- Минимальна сумма искажений квадратов расстояний между всеми точками данных и их «центром тяжести».
Визуализация данных является одним из наиболее широко используемых приложений метода главных компонент и его нелинейных обобщений[1]
Компрессия изображений и видео
Для уменьшения пространственной избыточности пикселей при кодировании изображений и видео используется линейные преобразования блоков пикселей. Последующие квантования полученных коэффициентов и кодирование без потерь позволяют получить значительные коэффициенты сжатия. Использование преобразования PCA в качестве линейного преобразования является для некоторых типов данных оптимальным с точки зрения размера полученных данных при одинаковом искажении [1]. На данный момент этот метод активно не используется, в основном из-за большой вычислительной сложности. Также сжатия данных можно достичь отбрасывая последние коэффициенты преобразования.
Подавление шума на изображениях [1]
Основная суть метода — при удалении шума из блока пикселей представить окрестность этого блока в виде набора точек в многомерном пространстве, применить к нему PCA и оставить только первые компоненты преобразования. При этом предполагается, что в первых компонентах содержится основная полезная информация, оставшиеся же компоненты содержат ненужный шум. Применив обратное преобразование после редукции базиса главных компонент, мы получим изображение без шума.
Индексация видео
Основная идея — представить при помощи PCA каждый кадр видео несколькими значениями, которые в дальнейшем будут использоваться при построении базы данных и запросам к ней. Столь существенная редукция данных позволяет значительно увеличить скорость работы и устойчивость к ряду искажений в видео.
Биоинформатика
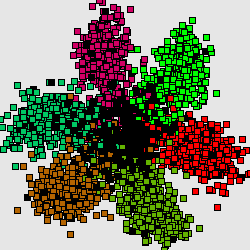
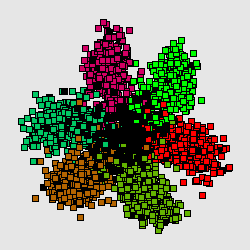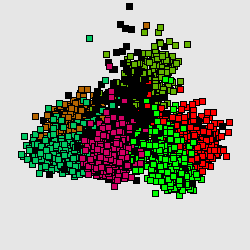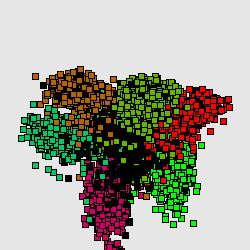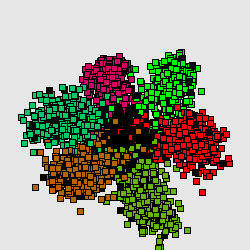
Метод главных компонент интенсивно используется в биоинформатике для сокращения размерности описания, выделения значимой информации, визуализации данных и др. Один из распространнённых вариантов использования — анализ соответствий (англ. Correspondence Analysis)[1][1]. На иллюстрациях (Рис. А, Б) генетический текст (см. статью Трансляция (биология)) представлен как множество точек в 64-мерном пространстве частот триплетов. Каждая точка соответствует фрагменту ДНК в скользящем окне длиной 300 нуклеотидов (ДНК-блуждание). Этот фрагмент разбивается на неперекрывающиеся триплеты, начиная с первой позиции. Относительные частоты этих триплетов в фрагменте и составляют 64-мерный вектор. На Рис. А представлена проекция на первые 2 главные компоненты для генома бактерии Streptomyces coelicolor. На Рис. Б представлена проекция на первые 3 главные комроненты. Оттенками красного и коричневого выделены фрагменты кодирующих последовательностей в прямой цепи ДНК, а оттенками зеленого выделены фрагменты кодирующих последовательностей в обратной цепи ДНК. Черным помечены фрагменты, принадлежащие некодирующей части. Анализ методом главных компонент большинства известных бактериальных геномов представлен на специализированном сайте[1].
Хемометрика
Метод главных компонент — один из основных методов в хемометрике (англ. Chemometrics). Позволяет разделить матрицу исходных данных X на две части: «содержательную» и «шум». По наиболее популярному определению [1] «Хемометрика — это химическая дисциплина, применяющая математические, статистические и другие методы, основанные на формальной логике, для построения или отбора оптимальных методов измерения и планов эксперимента, а также для извлечения наиболее важной информации при анализе экспериментальных данных».
Психодиагностика
Психодиагностика является одной из наиболее разработанных областей приложения метода главных компонент [1]. Стратегия использования основывается на гипотезе об автоинформативности экспериментальных данных, которая подразумевает, что диагностическую модель можно создать путем аппроксимации геометрической структуры множества объектов в пространстве исходных признаков. Хорошую линейную диагностическую модель удается построить, когда значительная часть исходных признаков внутренне согласованна. Если эта внутренняя согласованность отражает искомый психологический конструкт, то параметры линейной диагностической модели (веса признаков) дает метод главных компонент.
Общественные науки
Метод главных компонент — один из основных инструментов эконометрики. Он применяется для: (1) наглядного представления данных; (2) обеспечения лаконизма моделей, упрощения счета и интерпретации; (3) сжатия объемов хранимой информации. Метод обеспечивает максимальную информативность и минимальное искажение геометрической структуры исходных данных. В социологии метод небходим для решения первых двух основных задач[1]: (1) анализ данных (описание результатов опросов или других исследований, представленных в виде массивов числовых данных); (2) описание социальных явлений (построение моделей явлений, в том числе и математических моделей). В политологии метод главных компонент был основным инструментом проекта «Политический Атлас Современности»[1] для линейного и нелинейного анализа рейтингов 192 стран мира по пяти специально разработанным интегральным индексам (уровня жизни, международного влияния, угроз, государственности и демократии). Для картографии результатов этого анализа разработана специальная ГИС (Геоинформационная система), объединяющая географическое пространство с пространством признаков.
Сокращение размерности динамических моделей
Проклятие размерности (англ. Curse of dimensionality}}) затрудняет моделирование сложных систем. Сокращение размерности модели — необходимое условие успеха моделирования. Для достижения этой цели создана разветвленная математическая технология. Метод главных компонент также используется в этих задачах (часто под названием истинное или собственное ортогональное разложение — англ. proper orthogonal decomposition (POD)). Например, при описании динамики турбулентности динамические переменные — поле скоростей — принадлежат бесконечномерному пространству (или, если предствлять поле его значениями на достаточно мелкой сетке, — конечномерному пространству большой размерности). Можно набрать большую коллекцию мгновенных значений полей и применить к этому множеству многомерных «векторов данных» метод главных компонент. Эти главные компоненты называются также эмпирические собственные векторы. В некоторых случаях (структурная турбулентность) метод дает впечатляющее сокращение размерности[1] Другие области применения этой техники сокращения динамических моделей чрезвычайно разнообразны — от теоретических основ химической технологии (англ. chemical engineering science) до океанологии и климатологии.
Литература
Основные руководства (стандарт де-факто)
- Айвазян С. А., Бухштабер В. М., Енюков И. С., Мешалкин Л. Д. Прикладная статистика. Классификация и снижение размерности.— М.: Финансы и статистика, 1989.— 607 с.
- Рао С. Р., Линейные статистические методы и их применения.— М.: Наука (Физматлит), 1968.— 548 с.
- Jolliffe I.T. Principal Component Analysis, Series: Springer Series in Statistics, 2nd ed., Springer, NY, 2002, XXIX, 487 p. 28 illus. ISBN 978-0-387-95442-4
Сборник современных обзоров
- Gorban A. N., Kegl B., Wunsch D., Zinovyev A. Y. (Eds.), Principal Manifolds for Data Visualisation and Dimension Reduction, Series: Lecture Notes in Computational Science and Engineering 58, Springer, Berlin — Heidelberg — New York, 2007, XXIV, 340 p. 82 illus. ISBN 978-3-540-73749-0 (а также онлайн).
Ссылки
- A tutorial on Principal Components Analysis, Lindsay I Smith, 2002
- Нелинейный метод главных компонент (сайт-библиотека)
Примечания

