Однослойные сети RBF для решения задач регрессии (пример)

Материал из MachineLearning.

Версия от 12:15, 3 октября 2013; Mikethehuman (Обсуждение | вклад)

(разн.) ← Предыдущая | Текущая версия (разн.) | Следующая → (разн.)

Цель работы - решить задачу регрессии с помощью сети радиальных базисных функций и исследовать некоторые свойства алгоритма.

Радиальная функция - это функция $f(x)$ , зависящая только от расстояния между $x$ и фиксированной точкой пространства $X$ . В данной работе используются гауссианы $p_j(x) = N(x; \mu _j ,\Sigma _j)$ , которые можно представить в виде $p_j(x) = N_j exp(-\frac{1}{2} \rho _j (x, \mu _j)$
где $N_j = (2\pi)^ {-\frac{n}{2}}(\sigma _{j1}, \dots ,\sigma _{jn})^{-1}$ - нормировочный множитель,
$\rho _j(x, x')$ - взвешенная евклидова метрика в $n$ -мерном пространстве $X$ :
$~\rho (x, x') = \sum ^n _{d = 1} \sigma ^{-2} _{jd} |\xi _d - \xi _d '|$ ,
$x = (\xi _1, . . . ,\xi _n), x' = (\xi _1 ', . . . , \xi _n')$ .
Сеть радиальных базисных функций - нейронная сеть прямого распространения сигнала, которая содержит промежуточный (скрытый) слой радиально симметричных нейронов. Такой нейрон преобразовывает расстояние от данного входного вектора до соответствующей ему фиксированной точки пространства $X$ по некоторому нелинейному закону, заданному радиальной функцией. В данной статье мы рассмотрим применение этой нейронной сети к решению задачи регрессии с помощью восстановления смесей распределений.

Содержание

1 Постановка задачи
2 Описание алгоритма
- 2.1 Разделение смеси рапределений
- 2.2 Восстановление регрессии
3 Вычислительный эксперимент
4 Исходный код
5 См. также
6 Литература

Постановка задачи

Задана выборка — множество $X^N=\{{x}_1,\ldots,{x}_N|x\in\R^M\}$ значений свободных переменных и множество $\{y_1,\ldots, y_N| y\in\R\}$ соответствующих им значений зависимой переменной. Предполагается, что на множестве объектов задана плотность распределения $p(x)$ , представимая в виде смеси распределений - $k$ гауссиан с параметрами $\mu_j$ и $\Sigma_j$ : $p(x) = \sum_{j=1}^k w_jp_j(x) = \sum_{j=1}^k w_jN(x;\mu_j,\Sigma_j).$
$N(x;\mu_j,\Sigma_j) = \frac{1}{\sqrt{(2\pi)^ndet\Sigma_j}}e^{-\frac{1}{2}(x-\mu_j)\Sigma_j^{-1}(x-\mu_j)^{T}}$
Требуется решить задачу регрессии с помощью однослойной сети RBF, параметрами которой являются
$k$ - число компонент смеси,
$w_j$ - веса компонент,
$\theta_j=(\mu_j,\Sigma_j)$ - центры и дисперсия компонент,
$y(\mu_j)=Y_j$ - значения зависимой переменной в центрах компонент.
Смесь распределений требуется восстановить с помощью EM-алгоритма с добавлением компонент.
Таким образом решается задача регрессии с помощью однослойной сети RBF, обучаемой с помощью EM-алгоритма с добавлением компонент.

Описание алгоритма

Разделение смеси рапределений

Настройка параметров RBF-сети происходит с помощью EM-алгоритма с добавлением компонент. Идея EM-алгоритма заключается во введении вспомогательного вектора скрытых переменных $G$ : $g_{ij} = P(\theta_j |x_i)$ . С одной стороны, он может быть вычислен, если известны значения вектора параметров $\theta$ , с другой стороны, поиск максимума правдоподобия сильно упрощается, если известны значения скрытых переменных. EM-алгоритм состоит из итерационного повторения двух шагов. На E-шаге вычисляется ожидаемое значение (expectation) вектора скрытых переменных $G$ по текущему приближению вектора параметров $\theta$ . На М-шаге решается задача максимизации правдоподобия (maximization) и находится следующее приближение вектора $\theta$ по текущим значениям векторов $G$ и $\theta$ .

Если число компонент смеси заранее неизвестно, то применяется EM-алгоритм с последовательным добавлением компонент. Его идея заключается в том, что если данные описаны смесью $k$ компонент, то можно добавить в смесь $(k+1)$ -ю компоненту, построенную на плохо описанных элементах.
Элемент $x_i$ считается плохо описанным, если его правдободобие $p(x_i)<\frac{\max_i {\{p(x_i)\}}}{R}$ , $R$ - параметр.
Далее на смеси из $(k+1)$ -ой компоненты запускается EM-алгоритм.

Для более подробного описания см.

Восстановление регрессии

Значения зависимой переменной в центрах компонент
$Y_j=y(\mu_j)=\frac{\sum_{i=1}^N y_ip_j(x_i)}{\sum_{i=1}^N p_j(x_i)}$
Значение $a(x)$ для произвольного $x \in R^m$ получим, используя формулу Надарая-Ватсона
$a(x)=\frac{\sum_{j=1}^k Y_jw_jp_j(x)}{\sum_{j=1}^k w_jp_j(x)}$
Эта формула интуитивно очевидна: значение $a(x)$ есть среднее $Y_j$ по центрам компонент с учетом вероятности того, что объект $x$ принадлежит $j$ -ой компоненте смеси.

Вычислительный эксперимент

Эксперименты проводились на модельных данных. $x \in R$ , т.е. один признак. Цель эксперимента - проверить работу описанного алгоритма, исследовать его сходимость.

Пример 1

Задана функция $y=x$ . Выборка $X^N$ сгенерирована случайно согласно следующему распределению: несколько нормальных классов с центрами в точках $\mu_j=j$ , $j=1\ldots4$ и нормальной дисперсией $\sigma_j=0.03$ . В каждом классе $150$ объектов. К значениям $y_1,\ldots, y_N$ добавлен нормальный шум с дисперсией $0.05$
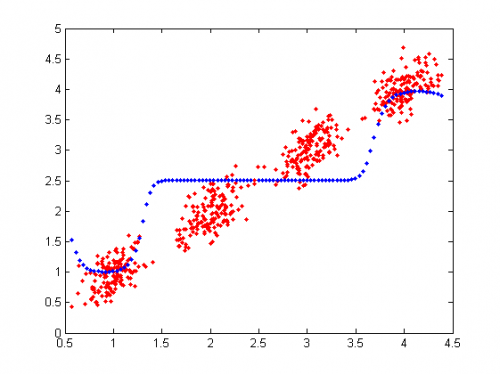
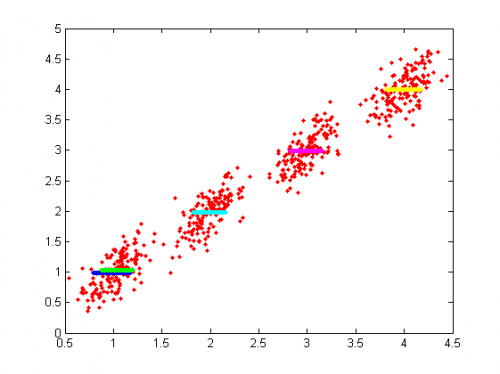
Красный цвет - данные, синий - полученная в результате работы алгоритма зависимость $y(x)$

Результат разделения смеси распределений (середина полосы-центр компоненты $\mu_j$ , полуширина - корень из дисперсии компоненты $\sigma_j$ , координата по оси $y$ - значение зависимой переменной в центре компоненты $Y_j$ ):

Найдено 4 компоненты
[4.0402; 2.5110; 2.5089; 0.9861] - центры,
[0.0271; 0.4256; 0.4257; 0.0188] - дисперсии ,
[0.2257; 0.1908; 0.3537; 0.2299] - веса.

Вторая и третья компоненты совпадают, т.е. на самом дела найдено всего 3 компоненты, одна из которых разбита на 2. Дальнейшее разделение смеси приводит только к большему разделению этой компоненты.
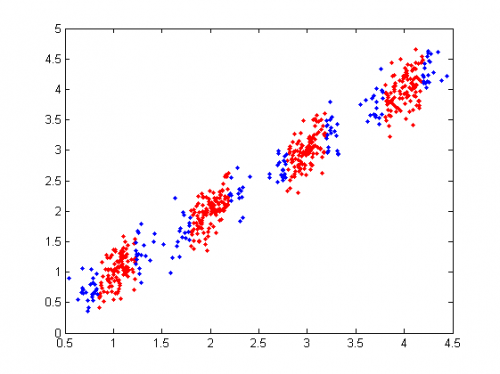
Плохо описанные элементы на следующем шаге(синим цветом):

Видно, что центр новой компоненты из плохо описанных элементов попадает в точку $2.5$ , и в результате EM-итераций новя компонента не отделяется от уже существующих там второй и третей компонент.

Пример 2

Те же данные, что и в примере 1, попытка отделить новую компоненту от старой. Если она попадает в то место, где уже есть старая, то перед запуском EM-итераций сдвигаем ее центр на небольшую величину.

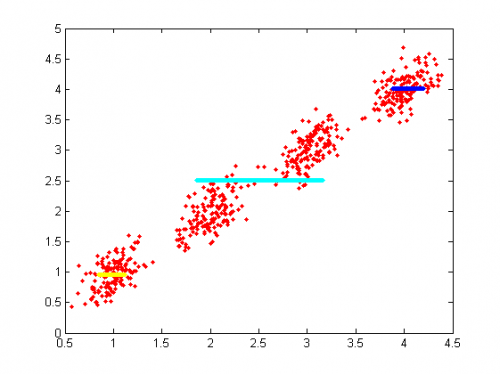
Результат разделения смеси распределений

Плохо описанные элементы:

Как видно, совпадения компонент уже нет. Но дальнейшее разделение смеси невозможно, т.к. ковариационная матрица одной из компонент $\Sigma_j$ оказалась вырожденной, а для подсчета правдободобия требуется ее обращать.

Пример 3

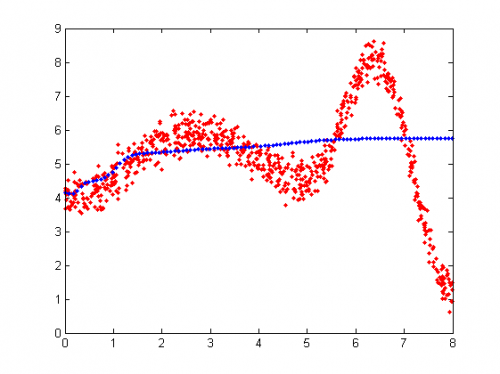
Выборка $X^N$ сгенерирована случайно согласно равномерному распределению. К значениям $y_1,\ldots, y_N$ добавлен нормальный шум с дисперсией $0.01$

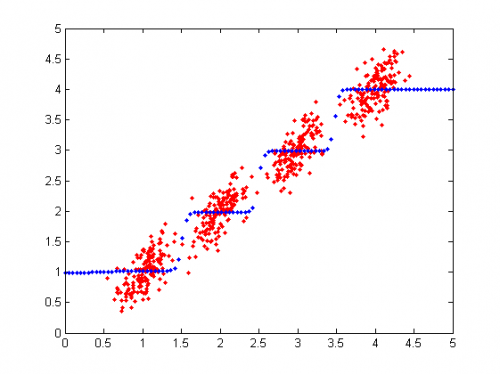
Результат разделения смеси распределений

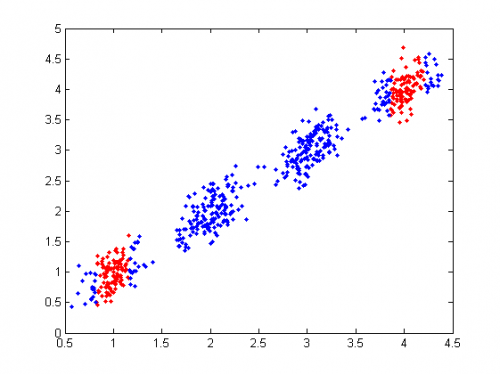
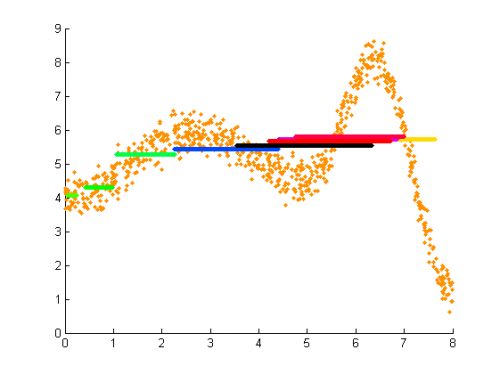
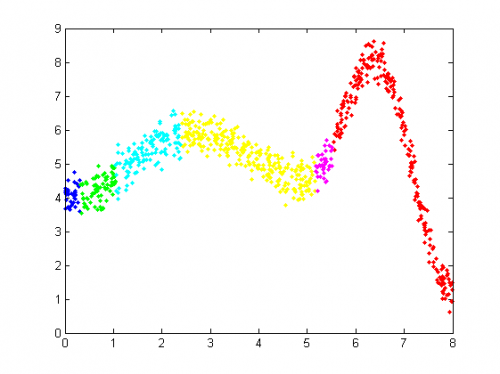
На следующем графике покажем кластеризацию на основе разделения смеси: каждый элемент $x_i$ отнесен к компоненте
$j_i$ , вероятность принадлежности к которой максимальна с учетом весов, т.е.
$j_i=arg \max_{j=1\ldots k} \{w_jp_j(x_i)\}$ , $i=1\ldots N$ .

Видно, что для лучшего восстановления регрессии требуется продолжить разделение смеси, в частности, разделить изображенные на рисунке красным и желтым цветом компоненты на несколько.

Исходный код

Скачать код MATLAB можно здесь: RBFlearn.m

См. также

Литература

Хайкин, Саймон. Нейронные сети: полный курс, 2-е изд., испр. : Пер. с англ. - М. : ООО "И.Д. Вильямс", 2006. - 1104 с. : ил. - Парал. тит. англ. ISBN 5-8459-0890-6 (рус.)
К. В. Воронцов, Лекции по линейным алгоритмам классификации и регрессии[[1]]