Метод Парзеновского окна (пример)

Материал из MachineLearning.

Версия от 12:33, 3 октября 2013; Mikethehuman (Обсуждение | вклад)

(разн.) ← Предыдущая | Текущая версия (разн.) | Следующая → (разн.)

Метод Парзеновского окна принадлежит к непараметрическим методам классификации и представляет собой одну из возможных реализаций байесовского подхода к решению задачи классификации. Он естественным образом возникает при предположении о байесовости вероятностных распределений объектов. В методе производится классификация объекта по находящимся на некотором расстоянии от него объектах с весом, зависящим от расстояния. Алгоритм имеет ряд параметров, которые будут более детально рассмотрены в последующих разделах.

Содержание

1 Постановка задачи разделения классов методом парзеновского окна
2 Алгоритм отыскания оптимальных параметров
3 Вычислительный эксперимент
- 3.1 Работа алгоритма на реальных данных
4 Исходный код
5 Смотри также
6 Литература

Постановка задачи разделения классов методом парзеновского окна

Пусть у нас задана выборка $\{(\mathbf{x}_i,y_i)\}_{i=1}^m$ , где $X^m$ = $\{\mathbf{x}_i\}_{i=1}^m$ - множество объектов, а $Y^m$ = $\{\mathbf{y}_i\}_{i=1}^m$ - множество ответов на этих объектах. Кроме того, задан объект $x_0$ , который небоходимо классифицировать с помощью алгоритма $a(x;X^{l},h)$ . Тогда если задана парзеновская оценка плотности $\hat{p}_{y,h}=\frac{1}{l_y V(h)}\sum_{i=1}^l {[}y_i = y{]} K\left(\frac{\ro{}(x,x_i)}{h}\right),$ где $V(h)$ - некоторая функция от ширины окна, а $l_y$ - дополнительный параметр, зависящий от класса, то задача состоит в том, что бы подобрать параметр $h$ , ширину окна, и $K$ , ядерную функцию, таким образом, что бы при классификации с помощью метода парзеновского окна функционал качества достигал бы своего максимума при работе алгоритма с заданными параметрами: $a(x;X^{l},h)=\arg \max_{y\in Y} \lambda_{y} \sum_{i=1}^l {[}y_i = y{]} K\left(\frac{\ro{}(x,x_i)}{h}\right).$

В этой формуле $\lambda_{y}$ - цена правильного ответа для каждого класса из $Y$

Алгоритм отыскания оптимальных параметров

Чтобы найти ширину окна и наиболее подходящий нам тип ядра, мы воспользуемся принципом максимального правдоподобия и исключением объектов по одному leave-one-out:

$h^{*}=\arg{ } \max_{h} \sum_{i=1}^l \log \hat{p}_h (x_i;X^{m}{/}x_i).$

То есть, мы будем восстанавливать значение класса для одного объекта из нашей выборки и максимизировать логарифм количества правильных ответов при исключении по очереди всех объектов выборки. Максимизация этого значения происходит по двум параметрам - ширине окна $h$ и типу ядерной функции. Ширину окна мы можем подобрать из некоторого диапазона $\delta{}H$ , полученного из эмпирических предположений. Ядро выбирается из нижеприведенного набора ядер:

#	ядро $K(r)$	формула
1	Епанечникова	$K_1(r)=E(r)=\frac{3}{4}(1-r^2){[}{\|}r{\|}<=1{]}$
2	Квартическое	$K_2(r)=Q(r)=\frac{15}{16}(1-r^2)^2{[}{\|}r{\|}<=1{]}$
3	Треугольное	$K_3(r)=T(r)=(1-{\|}r{\|}){[}{\|}r{\|}<=1{]}$
4	Гауссовское	$K_4(r)=G(r)=(2\pi)^{(-\frac{1}{2})}exp(-\frac{1}{2}r^2)$
5	Прямоугольное	$K_5(r)=\Pi(r)=\frac{1}{2}{[}{\|}r{\|}<=1{]}$

Получившееся выражение имеет достаточно понятный вид:

$(h^{*},K^{*}_s(r))=\arg{ } \max_{\small s\in\{1,2,3,4,5\}} \max_{h\in\delta{}H} \sum_{i=1}^l \log \hat{p}_h (x_i;X^{m}{/}x_i).$

Вычислительный эксперимент

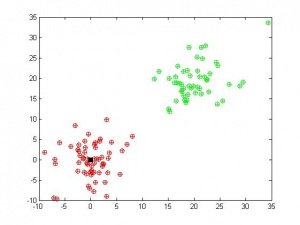
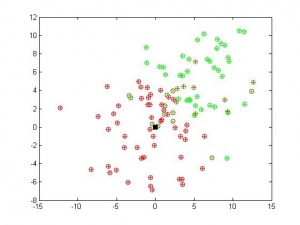
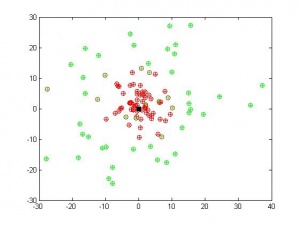
Вычислительный эксперимент был проведен на реальных и модельных данных. В качестве модельных данных были взяты точки из двух двумерных нормальных распределений с разными математическими ожиданиями и дисперсиями (соответственно, были получены два класса объектов). После запуска алгоритма порядка 30 раз были получены следующие результаты:

Код получения данных:

%NORMGENERATION generation of normal data in 2 classes with different
%parameteres to be described in V: V(1, 1) V(1, 2) parameters of normal
%distribution for first class; V(2, 1) V(2, 2) parameters of normal
%distribution for first class; V(1, 3) - number of properties; V(1, 4),
%V(2,4) - number of objects in first and second class
firstClass = random('normal', V(1, 1), V(1, 2), V(1, 3), V(1, 4));
secondClass = random('normal', V(2, 1), V(2, 2), V(1, 3), V(2, 4));
variables = [firstClass , secondClass];
responses = [ones(1, V(1, 4)), zeros(1, V(2, 4))];

Для каждой ядерной функции был проведен отдельный эксперимент, но из-за небольшого различия в результатах, мы их здесь не приводим. В каждом случае была использована своя матрица параметров двухмерного распределения $V=\{M_1,\sigma_1^2,m,n_1{;}M_2,\sigma_2^2,m,n_2\}$ , где $M_i$ - математическое ожидание для $i$ -го класса, $\sigma_i^2$ -дисперсия, $m=2$ - размерность пространства признаков, $n_i$ - количество элемнтов каждого класса

#	$\sigma_1^2$	$n_1$	$M_2$	$\sigma_2^2$	$n_2$
1	4	60	20	4	50
2	4	60	5	4	50
3	4	60	0	12	50

Мы видим, что при хорошо разделимых классах, наш алгоритм работает замечательно при правильно подобранном значение $k$ и любом ядре.

Во втором случае классы были сближены, что привело к некоторому неустранимому числу ошибок.

В третьем случае были взяты два класса с одинаковыми математическими ожиданиями, но разными дисперсиями. Алгоритм достаточно хорошо разделил и их.

Кроме того, в каждом случае был проведен эксперимент для различных ядерных функций. Результаты - в таблице ниже:

#	ядро $K(r)$	Эксперимент 1	Эксперимент 2	Эксперимент 3
1	Епанечникова	0%	13,64%	20,91%
2	Квартическое	0%	13,64%	20,00%
3	Треугольное	0%	13,64%	20,00%
4	Гауссовское	0%	13,64%	17,27%
5	Прямоугольное	0%	12,73%	21,82%

На пересечении строки с названием ядра и столба с номером эксперимента - процент ошибок для соответствующей ядерной функций и эксперимента. Как видно из таблицы, результаты для разных ядерных функций отличаются незначительно.

Работа алгоритма на реальных данных

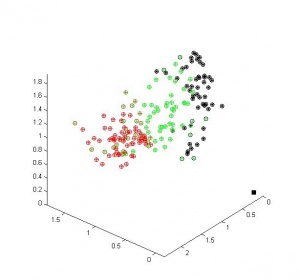
В качестве реальной задачи была выбрана задача классификации происхождения вина (3 класса) по трем признакам: общее содержание фенолов (Total phenols), содержание флавоноидных (Flavanoids) и нефлавоноидных (Nonflavanoid phenols) фенолов. Данные хорошо разделимы по этим трем признакам.

Мы видим, что наш алгоритм достаточно хорошо разделил объекты на три класса, сделав очень небольшое число ошибок.

Исходный код

Скачать листинги алгоритмов можно здесь [1]

Смотри также

Литература

Воронцов К. В. Лекции по линейным алгоритмам классификации.
Christopher M. Bishop Pattern Recognition and Machine Learning. — Hardcover. — 2006. — 740 с.
Pascal Vincent, Yoshua Bengio Manifold Parzen Windows. — 2002.
Erik Mcdermott, Shigeru Katagiri A Parzen Window Based Derivation Of Minimum Classification Error From The Theoretical Bayes Classification Risk. — 2002.