Статистический анализ данных (курс лекций, К.В.Воронцов)/2013

Материал из MachineLearning.

Версия от 08:03, 21 октября 2013; Riabenko (Обсуждение | вклад)

(разн.) ← Предыдущая | Текущая версия (разн.) | Следующая → (разн.)

Содержание

1 Оценки
2 Задание 1. Исследование свойств одномерных статистических критериев на модельных данных
- 2.1 Пример задания
- 2.2 Задания
  - 2.2.1 Анализ поведения схожих критериев
  - 2.2.2 Анализ устойчивости критериев к нарушению предположений
3 Ссылки

Оценки

Студент	#1 (1 балл)	#2 (2 балла)	Рецензирование #2 (1 балл)	#3 (2 балла)	Рецензирование #3 (1 балл)	Сумма
Березин Алексей	1
Борисов Михаил
Гавриков Михаил	1
Зак Евгений
Исмагилов Тимур
Кондрашкин Дмитрий	0.9
Куракин Александр	1
Лобачева Екатерина	1
Любимцева Мария	1
Малышева Екатерина	1
Меркулова Татьяна	1
Морозова Дарья
Нижибицкий Евгений	1
Новиков Максим	1
Огнева Дарья
Остапец Андрей	1
Потапенко Анна	1
Ромов Петр	0.9
Фонарев Александр	1
Шаймарданов Ильдар	1

Штраф за просрочку сдачи заданий начисляется из расчета 0.1 балла за сутки.
Задание считается сданным на момент получения проверяющим письма с отчётом (и кодом, если это указано в задании), при условии отсутствия необходимости внесения дополнений и исправлений.
Для допуска к экзамену необходимо сдать как минимум два задания, обязательно включая первое.

Задание 1. Исследование свойств одномерных статистических критериев на модельных данных

Необходимо провести исследование одного или нескольких классических критериев проверки статистических гипотез. Интерес представляет поведение достигаемого уровня значимости (p-value) как функции размера выборок и параметров распределения. В соответствии с индивидуальными параметрами задания необходимо указанным способом сгенерировать одну или несколько выборок из заданного распределения, выполнить проверку гипотезы при помощи соответствующего критерия, а затем многократно повторить эту процедуру для различных значений параметров. По результатам расчётов необходимо построить требуемые в задании графики, среди которых могут быть следующие:

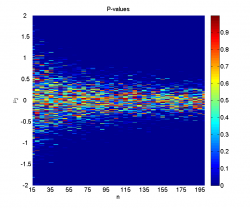
график зависимости достигаемого уровня значимости от значений параметров при однократном проведении эксперимента;
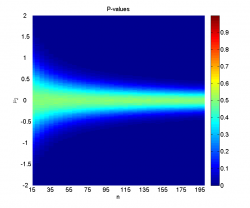
график зависимости достигаемого уровня значимости одного или двух критериев от значений параметров, усреднённого по большому количеству повторений эксперимента (например, по 1000 повторений);
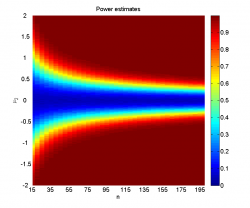
график с эмпирическими оценками мощности одного или двух критериев для разных значений параметров.

В качестве оценки мощности принимается доля отвержений нулевой гипотезы среди всех проверок. То есть, если эксперимент повторялся $k$ раз для каждого набора значений параметров, и в $m$ из $k$ случаев гипотеза была отвергнута на некотором фиксированном уровне значимости $\alpha$ (примем $\alpha=0.05$ ), оценкой мощности будет отношение $m/k.$

Необходимо сдать: выполненный в Tex или Microsoft Word отчёт с описанием алгоритма, построенными графиками и выводами (объяснение полученных результатов моделирования, границы применимости критерия и т.д.), а также код на R, Матлабе или Питоне, при запуске которого на экран выводятся графики, соответствующие имеющимся в отчёте.

Задание принимается до 23:59 19.10.

Пример задания

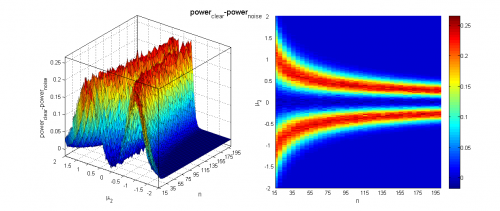
Исследуем чувствительность классического двухвыборочного критерия Стьюдента для проверки гипотезы однородности против альтернативы сдвига при зашумлении выборок наблюдениями, взятыми из равномерного распределения.

$X_1^n, \;\; X_{1i} \sim 0.9\cdot N(\mu_1,1)+ 0.1\cdot U\left[-5+\mu_1,5+\mu_1\right]$ — выборка длины $n$ из смеси стандартного нормального $N(\mu_1,1)$ и равномерного $U\left[-5+\mu_1,5+\mu_1\right]$ распределений с весами $0.9$ и $0.1$ соответственно (при генерации выборки используется случайный датчик — если его значение не превосходит $0.9$ , то добавляем в выборку элемент, взятый из нормального распределения, иначе — элемент, взятый из равномерного).

$X_2^n, \;\; X_{2i} \sim 0.9\cdot N(\mu_2,1)+ 0.1\cdot U\left[-5+\mu_2,5+\mu_2\right]$ — аналогичная выборка.

$H_0\,:\; \mu_1=\mu_2, \;\; H_1\,:\; \mu_1\neq\mu_2.$

$\mu_1=0, \;\; \mu_2=-2\,:\,0.01\,:\,2, \;\; n=15\,:\,5\,:\,200.$

При каждом значении $\mu_2$ выборки для разных значений $n$ генерируются независимо.

Значения достигаемого уровня значимости при однократной генерации выборок.

Значения достигаемого уровня значимости, усрёднённые по 3000 экспериментам.

Значения эмпирических оценок мощности критерия при проведении 3000 экспериментов $(\alpha=0.05).$

Заметим, что однократная генерация выборок даёт достаточно нестабильные результаты, не позволяя точно оценить границы области, где нулевая гипотеза отклоняется, поэтому и необходимо усреднение по большому числу экспериментов.

Видно, что при достаточно большой разнице между средними и большом размере выборок наличие шума не мешает уверенно отклонять гипотезу однородности. Когда, наоборот, разница между средними невелика (меньше 0.2-0.5 в зависимости от размера выборок), мощность близка к нулю, а среднее значение достигаемого уровня значимости колеблется около 0.5, что логично, так как его распределение при справедливости нулевой гипотезы равномерно на $[0,1]$ .

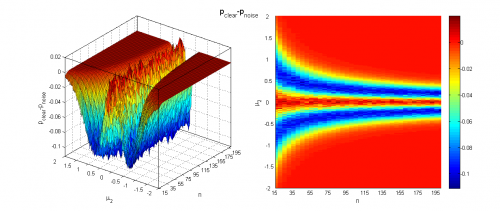
Чтобы оценить вклад зашумления выборок, оценим при всех значениях параметра мощность критерия и средний достигаемый уровень значимости на аналогичных выборках без шума и сравним результаты.

Разность средних достигаемых уровней значимости на выборках без шума и с шумом.

Разность эмпирических оценок мощности на выборках без шума и с шумом.

Видно, что наличие шума всё меньше влияет на работу критерия с ростом объёма выборок и разницы между их средними. Тем не менее, в некоторых областях изменения параметров потеря мощности из-за 10% зашумления может составлять до 20%, а средний достигаемый уровень значимости может быть выше на 0.1.

Отметим, что приведённые количественные выводы справедливы только для шума рассматриваемой структуры.

Задания

Анализ поведения схожих критериев

Требуется исследовать поведение указанной пары статистических критериев, подходящих для решения одной и той же задачи, сравнить мощность и достигаемые уровни значимости и сделать выводы о границах применимости критериев. Необходимо для каждого из критериев построить графики зависимости достигаемых уровней значимости и оценок мощностей от параметров, и показать, в каких областях изменения параметров предпочтительнее использовать тот или иной критерий. Для получения более гладких графиков рекомендуется применять оба критерия к одним и тем же выборкам, а не генерировать их отдельно для каждого критерия.

$X^n, \;\; X_i\sim Ber(p);$
$H_0\,:\, p=\frac{1}{2}, \;\; H_1\,:\, p\neq\frac{1}{2};$
$p=0.01\,:\,0.01\,:\,0.99, \;\; n=5\,:\,1\,:\,50.$

Гавриков: сравнить Z-критерий и точный критерий для доли.

Потапенко: сравнить критерии, основанные на доверительных интервалах Вальда и Уилсона (нулевая гипотеза отвергается на уровне значимости 5%, если 95% доверительный интервал для параметра не содержит $\frac{1}{2}$ ).

$X^n, \;\; X_i\sim N(\mu,\sigma);$
$H_0\,:$ среднее значение $X$ равно нулю, $H_1\,:$ среднее значение $X$ не равно нулю;
$\mu=-2\,:\,0.01\,:\,2, \;\; \sigma=1, \;\; n=5\,:\,1\,:\,50.$

Нижибицкий: сравнить одновыборочные T- и Z-критерии.

Зак: сравнить критерий знаковых рангов Уилкоксона и одновыборочный перестановочный критерий с суммой элементов в качестве статистики.

$X_1^{n}, \;\; X_{1i} \sim N(\mu_1, \sigma_1^2),\;\;X_2^{n}, \;\; X_{2i} \sim N(\mu_2, \sigma_2^2);$
$H_0\,:$ средние выборок равны, $\;H_1\,:$ средние выборок не равны;
$\mu_1=0, \;\; \sigma_1=1.$

Остапец: $\mu_2=-2\,:\,0.02\,:\,2, \;\; \sigma_2 = 0.5\,:\,0.01\,:\,2, \;\; n=30.$ Сравнить критерий Стьюдента для неизвестных равных дисперсий и двухвыборочный перестановочный критерий, основанный на статистике критерия Стьюдента для неизвестных равных дисперсий.

Морозова: $\mu_2=-2\,:\,0.02\,:\,2, \;\; \sigma_2 = 1, \;\; n=5\,:\,1\,:\,50.$ Сравнить критерий Аспина-Уэлша и двухвыборочный перестановочный критерий с разностью средних в качестве статистики.

Шаймарданов: $\mu_2=-2\,:\,0.02\,:\,2, \;\; \sigma_2 = 1, \;\; n=5\,:\,1\,:\,50.$ Сравнить критерий Уилкоксона-Манна-Уитни и критерий знаков.

$X_1^n, \;\; X_{1i} \sim 0.5\cdot N(0,1)+ 0.5\cdot U\left[-a,a\right], \;\; X_2^n, \;\; X_{2i} \sim 0.5\cdot N(0,\sigma^2)+ 0.5\cdot U\left[-a,a\right]$ — выборки длины $n$ из смеси нормального и равномерного $U\left[-a,a\right]$ распределений с равными весами (при генерации выборки используется случайный датчик — если его значение не превосходит $0.5$ , то добавляем в выборку элемент, взятый из нормального распределения, иначе — элемент, взятый из равномерного).
$H_0\,:$ дисперсии двух выборок равны, $\;H_1\,:$ дисперсии двух выборок не равны;
$\sigma=0.1\,:\,0.05\,:\,4.$

Кондрашкин: $a=3, \;\; n=10\,:\,5\,:\,100.$ Сравнить критерий Зигеля-Тьюки и критерий Брауна-Форсайта.

Борисов: $a=0.5\,:\,0.1\,:\,5, \;\; n=50.$ Сравнить критерий Брауна-Форсайта и критерий Фишера.

Огнева: $a=5, \;\; n=5\,:\,1\,:\,50.$ Сравнить WM-критерий и перестановочный критерий, основанный на статистике Али.

$X^n, \;\; X_i \sim p\cdot N(0,1)+ \left(1-p\right)\cdot U\left[-a,a\right]$ — выборка длины $n$ из смеси стандартного нормального $N(0,1)$ и равномерного $U\left[-a,a\right]$ распределений с весами $p$ и $1-p$ соответственно (при генерации выборки используется случайный датчик — если его значение не превосходит $p$ , то добавляем в выборку элемент, взятый из нормального распределения, иначе — элемент, взятый из равномерного).
$H_0\,:\; X_i \sim N, \;\;\; H_1\,:\; H_0$ неверна;
$n=10\,:\,5\,:\,100.$

Фонарев: $a=1, \;\; p=0\,:\,0.02\,:\,1.$ Сравнить критерий Шапиро-Уилка и критерий Колмогорова-Смирнова.

Лобачева: $a=2, \;\; p=0\,:\,0.02\,:\,1.$ Сравнить критерий омега-квадрат и критерий Жарка-Бера.

Исмагилов: $a=0.5\,:\,0.1\,:\,5, \;\; p=0.25.$ Сравнить критерий Колмогорова-Смирнова и критерий хи-квадрат.

Анализ устойчивости критериев к нарушению предположений

Требуется исследовать поведение указанного критерия в условиях нарушения лежащих в его основе предположений. Оценить мощность и достигаемый уровень значимости критерия при различных значениях параметров, сделать выводы об устойчивости

Одновыборочный критерий Стьюдента, нарушение предположения о нормальности.

$X^n, \;\; X_i \sim p\cdot N(\mu,1)+ \left(1-p\right)\cdot U\left[-a+\mu,a+\mu\right]$ — выборка длины $n$ из смеси нормального $N(\mu,1)$ и равномерного $U\left[-a+\mu,a+\mu\right]$ распределений с весами $p$ и $1-p$ соответственно (при генерации каждой выборки используется случайный датчик — если его значение не превосходит $p$ , то добавляем в выборку элемент, взятый из нормального распределения, иначе — элемент, взятый из равномерного).
$H_0\,:\; \mu=0, \;\; H_1\,:\; \mu\neq0.$

Березин: $\mu=-2\,:\,0.01\,:\,2, \;\; p=0.8, \;\; a=1, \;\; n=15\,:\,5\,:\,200.$

Малышева: $\mu=1, \;\; p=0\,:\,0.01\,:\,1, \;\; a=2, \;\; n=15\,:\,5\,:\,200.$

Ромов: $\mu=-2\,:\,0.01\,:\,2, \;\; p=0\,:\,0.01\,:\,1, \;\; a=1, \;\; n=150.$

Новиков: $\mu=0.5, \;\; p=0\,:\,0.01\,:\,1, \;\; a=0.1\,:\,0.1\,:\,5, \;\; n=100.$

Критерий Фишера для проверки равенства дисперсий, нарушение предположения о нормальности.

$X_1^n, \;\; X_{1i} \sim p_1\cdot N(0,\sigma_1^2)+ \left(1-p_1\right)\cdot U\left[-a,a\right]$ — выборка длины $n$ из смеси нормального $N(0,\sigma_1^2)$ и равномерного $U[-a,a]$ распределений с весами $p_1$ и $1-p_1$ соответственно (при генерации выборки используется случайный датчик — если его значение не превосходит $p_1$ , то добавляем в выборку элемент, взятый из нормального распределения, иначе — элемент, взятый из равномерного),
$X_2^n,\;\; X_{2i} \sim p_2\cdot N(0,\sigma_2^2)+ \left(1-p_2\right)\cdot U\left[-a,a\right]$ — аналогичная выборка,
$H_0\,:$ дисперсии двух выборок равны, $\;H_1\,:$ дисперсии двух выборок не равны;
$\sigma_1=2, \;\; \sigma_2=0.1\,:\,0.05\,:\,4.$