Участник:Vitsemgol/Биномиальное распределение одной случайной величины

Материал из MachineLearning.

Версия от 07:49, 15 ноября 2013; Vitsemgol (Обсуждение | вклад)

(разн.) ← Предыдущая | Текущая версия (разн.) | Следующая → (разн.)

**Биномиальное распределение**
Функция вероятности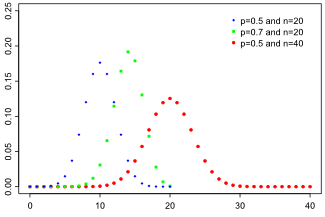
Функция распределения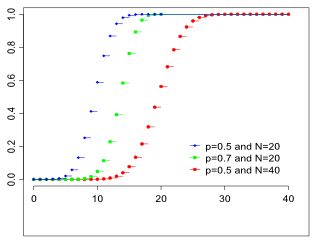
Параметры	$n \geq 0$ — число «испытаний» $0\leq p \leq 1$ — вероятность «успеха»
Носитель	$k \in \{0,\ldots,n\}\!$
Функция вероятности	${n \choose k}\,p^k q^{n-k} \!$
Функция распределения	$I_{1-p}(n-\lfloor k\rfloor, 1+\lfloor k\rfloor) \!$
Математическое ожидание	$np\!$
Медиана	одно из $\{[np]-1, [np], [np]+1\}$
Мода	$\lfloor (n+1)\,p\rfloor\!$
Дисперсия	$npq\!$
Коэффициент асимметрии	$\frac{1-2p}{\sqrt{npq}}\!$
Коэффициент эксцесса	$\frac{1-6pq}{npq}\!$
Информационная энтропия	$\frac12 \log_2 \big( 2\pi e\, np(1-p) \big) + O \left( \frac{1}{n} \right)$
Производящая функция моментов	$(q + pe^t)^n \!$
Характеристическая функция	$(q + pe^{it})^n \!$

Содержание

1 Определение
2 Основные свойства
3 Асимптотические приближения при больших
- 3.1 Приближение Пуассона
- 3.2 Нормальное приближение
4 Биномиальное распределение не может быть распределением одной случайной величины
- 4.1 Доказательство первое
- 4.2 Доказательство второе - Буняковского

Определение

Биномиальное распределение — дискретное распределение вероятностей одной случайной величины $X,$ принимающей целочисленные значения $k=0,1,\ldots,n$ с вероятностями:

$P(X=k)={n \choose k}p^k(1-p)^{n-k}.$

Данное распределение характеризуется двумя параметрами: целым числом $n>0,$ называемым числом испытаний, и вещественным числом $p,$ $0\le p\le 1,$ называемом вероятностью успеха в одном испытании. Биномиальное распределение — одно из основных распределений вероятностей, связанных с последовательностью независимых испытаний. Если проводится серия из $n$ независимых испытаний, в каждом из которых может произойти "успех" с вероятностью $p,$ то случайная величина, равная числу успехов во всей серии, имеет указанное распределение. Эта величина также может быть представлена в виде суммы $X=X_1+\cdots+X_n$ независимых слагаемых, имеющих распределение Бернулли.

Основные свойства

Характеристическая функция: $\phi(t)=(1+p(e^{it}-1))^n.$

Моменты:

Математическое ожидание: $MX=np.$
Дисперсия: $DX=np(1-p).$
Асимметрия: $\gamma_1=\frac{1-2p}{\sqrt{np(1-p)}};$ при $p=0.5$ распределение симметрично относительно центра $n/2.$

Асимптотические приближения при больших $n$

Если значения $n$ велики, то непосредственное вычисление вероятностей событий, связанных с данной случайной величиной, технически затруднительно. В этих случаях можно использовать приближения биномиального распределения распределением Пуассона и нормальным (приближение Муавра-Лапласа).

Приближение Пуассона

Приближение распределением Пуассона применяется в ситуациях, когда значения $n$ большие, а значения $p$ близки к нулю. При этом биномиальное распределение аппроксимируется распределением Пуассона с параметром $\lambda=np.$

Строгая формулировка: если $n\to\infty$ и $p\to 0$ таким образом, что $np\to\lambda,$ то

$P(X=k)\to\frac{\lambda^k}{k!}e^{-\lambda},\quad k=0, 1, 2, \ldots$

Более того, справедлива следующая оценка. Пусть $Y$ — случайная величина, имеющая распределение Пуассона с параметром $\lambda=np.$ Тогда для произвольного множества $B\subset\{0,1,2,\ldots\}$ справедливо неравенство:

$|P(X\in B) - P(Y\in B)|\le 2np^2.$

Нормальное приближение

Приближение нормальным распределением используется в ситуациях, когда $n\to\infty,$ а $p$ фиксировано. Это приближение можно рассматривать как частный случай центральной предельной теоремы, применение которой основано на представлении $X$ в виде суммы $n$ слагаемых. Приближение основано на том, что при указанных условиях распределение нормированной величины

$X'=\frac{X-MX}{\sqrt{DX}}=\frac{X-np}{\sqrt{npq},$ где $q=1-p,$

близко к стандартному нормальному.

Биномиальное распределение не может быть распределением одной случайной величины

Доказательство первое

Если биномиальное распределение одной случайной величины имеет математическое ожидание $MX=np$ , то при условии $n>\frac{1}{p}$ математическое ожидание биномиального распределения одной случайной величины будет превышать единицу $MX=np>1$ , что недопустимо, поскольку согласно второй аксиоме Колмогорова (см. Аксиоматика Колмогорова) сумма всех вероятностей любого распределения обязана быть равной единице.