Обсуждение участника:Strijov

Материал из MachineLearning.

Версия от 16:53, 14 октября 2008; Strijov (Обсуждение | вклад)

(разн.) ← Предыдущая | Текущая версия (разн.) | Следующая → (разн.)

Содержание

1 Временно: Метод главных компонент
2 Оформление статей
3 Для пополнения тулбокса
4 Список наблюдения
5 Вниманию участников
6 Метод главных компонент
7 С приездом
8 Спасибо!

Временно: Метод главных компонент

Метод главных компонент — способ снижения размерности пространства данных.

Он заключается в нахождении линейного ортогонального преобразования исходной матрицы данных в пространство меньшей размерности.

При этом выбираются такая ортогональная система координат, которая обеспечивает наименьшую потерю информации в исходных данных.

Последнее подразуменает минимальную среднеквадратичную ошибку при проекции данных в пространство заданной размерности.

Определение метода главных компонент

Векторы-строки матрицы исходных данных показаны звездочками. Красным крестом отмечен первый вектор-столбец матрицы вращения . Точками отмечены проекции векторов на новую систему координат. Сумма квадратов длин синих линий есть ошибка количество информации, утраченной при снижении размерности пространства.

Векторы-строки матрицы исходных данных $A$ показаны звездочками. Красным крестом отмечен первый вектор-столбец матрицы вращения $V$ . Точками отмечены проекции векторов на новую систему координат. Сумма квадратов длин синих линий есть ошибка — количество информации, утраченной при снижении размерности пространства.

Одной из задач аппроксимации является задача приближения множества векторов-строк $\mathbf{a}_i$ матрицы $A$ их проекциями на некоторую новую ортогональную систему координат.

Эта система отыскивается на множестве преобразований вращений $V$ начальной системы координат.

При этом множество аппроксимируемых векторов $\mathbf{a}_i$ , $i=1,...,m$ , отображается в новое множество векторов $\mathbf{z}_i$ , где $\mathbf{a}_i,\mathbf{z}_i\in\mathbb{R}^n$ .

Оператором отображения

$Z=A^TV$

является ортонормальная матрица $V$ , то есть $VV^T=I$ — единичная матрица.

Столбцы $Z$ называются главными компонентами матрицы $A$ . Матрица $V$ строится таким образом, что среднеквадратическая разность между векторами $\mathbf{a}_i$ и проекцией этих векторов на ортогональную систему координат, заданных $\mathbf{z}_i$ минимальна.

Наиболее удобным способом получения матрицы $V$ является сингулярное разложение матрицы $A$ :

$A=U\Lambda V^T.$

Метод главных компонент позволяет с помощью $k$ первых главных компонент можно восстановить исходную матрицу с минимальной ошибкой.

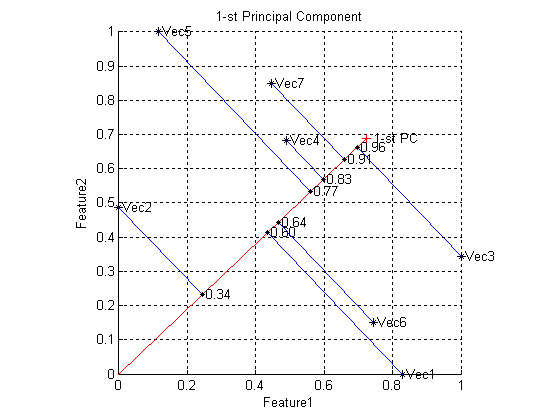
Критерий минимального значения суммы квадратов расстояния от векторов-столбцов матрицы данных до их проекций на первую главную компоненту называется критерием наибольшей информативности C.Р. Рао.

Кроме того, матрица $V$ выполняет декоррелирующее преобразование, называемое также преобразованием Карунена-Лоэва. В результате этого преобразования исчезает возможная корреляция между векторами-столбцами исходной матрицы $A$ . Рао было показано, что строки матрицы $V$ есть собственные векторы ковариационной матрицы $\Sigma=A^TA,$ где матрица $A$ центрирована — из каждого ее столбца вычтено среднее значение по этому столбцу.

Понятие наибольшей информативности

Рассмотрим $n$ -мерную случайную величину $A$ с ковариационной матрицей $\Sigma=A^TA$ . Обозначим $\mu_1,\dots,\mu_n$ — соответствующие собственные числа и $\mathbf{v}_1,\dots,\mathbf{v}_n$ — собственные векторы матрицы $\Sigma$ . Заметим, что собственные числа и элементы собственных векторов матрицы $\Sigma$ всегда действительны. Тогда по теореме о собственных числах $\Sigma=\sum_{i=1}^n\mu_i\mathbf{v}_i\mathbf{v}_i^T,$ $I=\sum_{i=1}^n\mathbf{v}_i\mathbf{v}_i^T,$ $\mathbf{v}_i^T{\Sigma}\mathbf{v}_i=\mu_i,$ $\mathbf{v}_i^T{\Sigma}\mathbf{v}_j=0,$ $i\neq{j}.$ (*) Случайная величина $\mathbf{z}_i=\mathbf{v}_i^TA$ называется $i$ -й главной компонентой случайной величины $A$ . Матрица вращения $V$ составлена из векторов-столбцов $\mathbf{v}_1,\ldots,\mathbf{v}_n$ . Матрица главных компонент $Z=A^TV$ имеет следующие свойства.

Смотри также

Литература

Рао С.Р. Линейные статистические методы и их применения. М.: Наука. 1968. — С. 530-533.
Айвазян С.А., Бухштабер В.М., Енюков И.С., Мешалкин Л.Д. Прикладная статистика. Классификация и снижение размерности. М.: Финансы и статистика. 1989.
Jolliffe I.T. Principal Component Analysis, Springer Series in Statistics. Springer. 2002.
Pearson, K. (1901). "On Lines and Planes of Closest Fit to Systems of Points in Space". Philosophical Magazine 2 (6): 559–572. [1]

Внешние ссылки

Нелинейный метод главных компонент
Principal components analysis at wikipedia.org
[http://ru.wikipedia.org/wiki/%D0%9C%D0%B5%D1%82%D0%BE%D0%B4_%D0%B3%D0%BB%D0%B0%D0%B2%D0%BD%D1%8B%D1%85_%D0%BA%D0%BE%D0%BC%D0%BF%D0%BE%D0%BD%D0%B5%D0%BD%D1%82 Метод главных компонент на

wikipedia.org]

Оформление статей

В статье обязательно должны присутствовать:

начальное определение, которое четко позиционирует понятие в рамках направления, сформулированное таким образом, чтобы оно было понятно и стороннему человеку, имеющему общую математическую подготовку;
категории - это единственный реальный инструмент поиска статей, кроме поиска по названию;
ссылки из своей статьи на другие и из других статей на текущую; ссылаться при этом можно и на пока еще не созданные статьи

Для пополнения тулбокса

Вадим, теперь есть возможность использовать шаблон {{S}} для установки правильных инициалов в статьях. Например, {{S|В. В. Стрижов}} даст такой результат В. В. Стрижов. --Yury Chekhovich 18:52, 12 февраля 2008 (MSK)

Список наблюдения

Рекомендую в настройках в закладке "Список наблюдения" включить следующие галочки "Добавлять созданные мной страницы в список наблюдения" и "Добавлять изменённые мной страницы в список наблюдения". Тае удобнее следить за изменениями на страницах, которые правил. --Yury Chekhovich 13:09, 14 февраля 2008 (MSK)

Вниманию участников

Появилась страница Вниманию участников предназначенная для общения участников по проекту. Предлагаю все идеи и проблемы вносить туда. --Yury Chekhovich 13:51, 29 февраля 2008 (MSK)

Метод главных компонент

Вадим, я обнаружил пустую эту пустую статью созданную участником Vadim Strijov :). Кинул туда буквально одно предложение, чтобы она не была пустой. У тебя нет желания её написать? Можно использовать и этот материал из Википедии. --Yury Chekhovich 10:33, 5 марта 2008 (MSK)

Уважаемый Вадим Викторович, я закачал материал из Википедии в Метод главных компонент, начал собирать подзаголовки для расширения. Устойчивость главных компонент, Сколько главных компонент нужно оставлять, Анализ соответствий ... . Добавьте и Вы свои пожелания, пригласите также коллег.--Agor153 14:57, 2 июля 2008 (MSD)

- Да, тут Андрей Зиновьев на пару недель из Парижа приехал в Россию. Мне удалось с ним связаться и спросить, не возражает ли он против публикации его книги "Визуализация многомерных данных" (2000 г.) на Вашем ресурсе. Он не возражает. А оно Вам надо? (Закономерный и своевременный вопрос ;).)--Agor153 02:12, 3 июля 2008 (MSD)

Спасибо! Да, оно нам надо. Опубликуем. Есть вот такой вопрос. Так как сайт поддерживают официальные организации: РФФИ, Форексис, ВЦ, то мы не должны нарушать авторские права. Мы должны будем поставить заметку, что автор согласен с публикацией и e-mail автора. И вопрос к Вам и к Андрею Зиновьеву: если книга издавалась, то какие права на нее имеет издательство? Разрешит ли оно такую публикацию? --Strijov 11:40, 3 июля 2008 (MSD)

ОК, попробую связаться. Думаю, что с издательством пробем не будет - но пусть он спросит. Все контакты займут, вероятно, несколько недель. (Эти "французские" ученые летом путешествуют вовсю, да и провинциальное российское издательство, вероятно, тоже отдыхает :).)--Agor153 14:06, 3 июля 2008 (MSD)

Здравствуйте, меня зoвут Андрей Зиновьев. Отвечаю на вопрос: на книге стоят два копирайта "Андрей Зиновьев" и "Институт Вычислительного Моделирования СО РАН". Я даю полное согласие на использование файла книги, который можно взять здесь http://pca.narod.ru/ZinovyevBook.pdf. С издательством не будет никаких проблем, они претензий на копирайт не имеют. --zinovyev 18:00, 12 августа 2008 (MSD)

Андрей, большое спасибо! --Strijov 01:53, 17 августа 2008 (MSD)

С приездом

Смотрю, ты сразу же рьяно взялся за дело :)) --Yury Chekhovich 18:52, 16 марта 2008 (MSK)

Спасибо!

--Strijov 19:32, 16 марта 2008 (MSK)

Источник — «http://machinelearning.ru/wiki/index.php?title=%D0%9E%D0%B1%D1%81%D1%83%D0%B6%D0%B4%D0%B5%D0%BD%D0%B8%D0%B5_%D1%83%D1%87%D0%B0%D1%81%D1%82%D0%BD%D0%B8%D0%BA%D0%B0:Strijov»