Метод покоординатного спуска
Материал из MachineLearning.
Содержание |
Постановка задачи
Рассмотрим задачу поиска минимума функции , записываемую в виде:
Метод покоординатного спуска (Метод Гаусса-Зейделя)
Алгоритм
Вход: функция
Выход: найденная точка оптимума
- Инициализация некоторым значением
- повторять:
- для
- фиксируем значения всех переменных кроме
, получая одномерную функцию
- проводим одномерную оптимизацию по переменной
, любым методом одномерной оптимизации
- если выполен критерий останова, то возвращаем текущее значение
- фиксируем значения всех переменных кроме
- для
Критерий останова
Критерии остановки процесса приближенного нахождения минимума могут быть основаны на различных соображениях. Некоторые из них:
Здечь --- значение, полученное после
-го шага оптимизации.
Сходимость метода
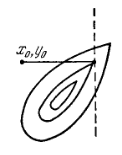
Легко убедится, что существуют функции, когда метод координатного спуска не приводит даже в локальный оптимум.
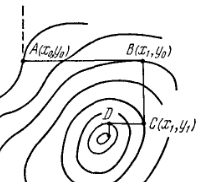
Пусть линии уровня образуют истинный овраг (рис.2), когда спуск по любой координате приводит на <<дно>> оврага, а любое движение по следующей координате (пунктирная линия) ведет на подъем. Никакой дальнейший спуск по координатам в данном случае невозможен, хотя минимум еще не достигнут.
Теорема о сходимости метода покоординатного спуска.
Для простоты рассмотрим функцию двух переменных . Выберем некоторое началное приближение
и проведем линию уровня через эту точку. Пусть в области
, ограниченной этой линией уровня, выполняются неравенства, означающий положительную определенность квадратичной формы:
Тогда спуск по координатам сходится к минимуму из данного начального приближения, причем линейно.
Числовые примеры
Рекомендации программисту
Заключение
Ссылки
Список литературы
- А.А.Самарский, А.В.Гулин. Численные методы. Москва «Наука», 1989.
- Н.С.Бахвалов, Н.П.Жидков, Г.М.Кобельков. Численные методы. Лаборатория Базовых Знаний, 2003.
- Н.Н.Калиткин. Численные методы. Москва «Наука», 1978.