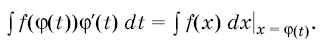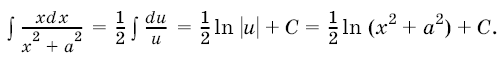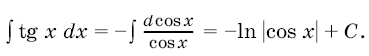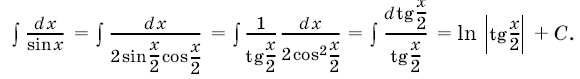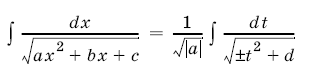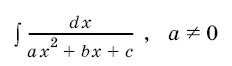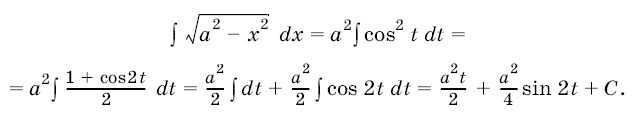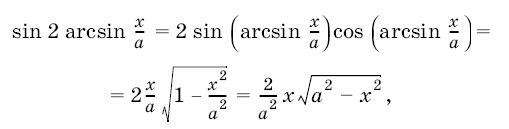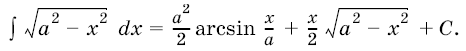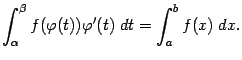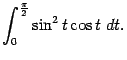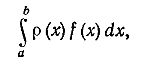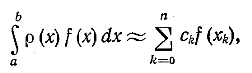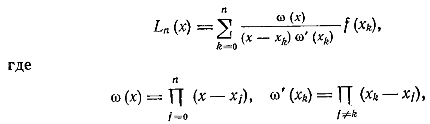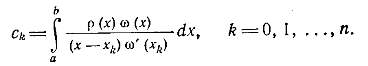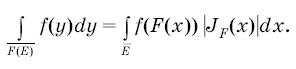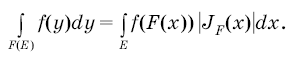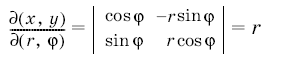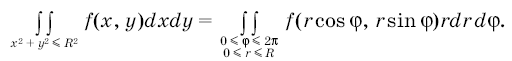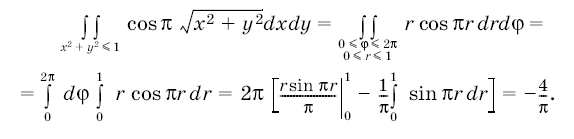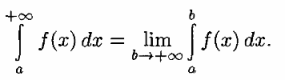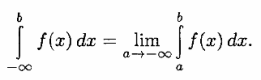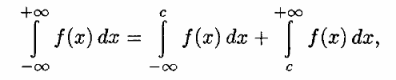Участник:Пасконова Ольга/Песочница
Материал из MachineLearning.
Содержание |
Формулы для определителя
1. Если матрица невырожденная, то
и
Знак плюс или минус дается определителем матрицы (или
) и зависит от того, является число перестановок строк в приведении четным или нечетным. Для треугольных сомножителей имеем
и
2.
Формула замены переменных в неопределенном интеграле
Рассмотрим свойство неопределенного интеграла, часто оказывающееся полезным при вычислении первообразных элементарных функций.
Теорема.
Пусть функции и
определены соответственно на промежутках
и
, причем
. Если функция
имеет на
первообразную
и, следовательно,
а функция дифференцируема на
, то функция
имеет на
, первообразную
и
Формула (1) называется формулой интегрирования подстановкой, а именно подстановкой . Это название объясняется тем, что если формулу (2) записать в виде
то будет видно, что, для того чтобы вычислить интеграл ![]() ), можно сделать подстановку
), можно сделать подстановку , вычислить интеграл
и затем вернуться к переменной
, положив
.
Примеры.
1. Для вычисления интеграла естественно сделать подстановку
, тогда
2. Для вычисления интеграла 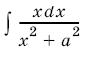 удобно применить подстановку
удобно применить подстановку
:
3. При вычислении интегралов вида ![]() полезна подстановка
полезна подстановка
:
Например,
Иногда, прежде чем применить метод интегрирования подстановкой, приходится проделать более сложные преобразования подынтегральной функции:
Отметим, что формулу (2) бывает целесообразно использовать и в обратном порядке, т.е. справа палево. Именно, иногда удобно вычисление интеграла с помощью соответствующей замены переменного
свести к вычислению интеграла
![]() (если этот интеграл в каком-то смысле «проще» исходного).
(если этот интеграл в каком-то смысле «проще» исходного).
В случае, когда функция имеет обратную
, перейдя в обеих частях формулы (2) к переменной
с помощью подстановки
и поменяв местами стороны равенства, получим
Эта формула называется обычно формулой интегрирования заменой переменной.
Для того чтобы существовала функция , обратная
, в дополнение к условиям теоремы достаточно, например, потребовать, чтобы на рассматриваемом промежутке
функция
была строго монотонной. В этом случае, существует однозначная обратная функция
.
4. Интегралы вида 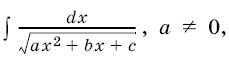 в том случае, когда подкоренное выражение неотрицательно на некотором промежутке, легко сводятся с помощью заме¬ны переменного к табличным.
в том случае, когда подкоренное выражение неотрицательно на некотором промежутке, легко сводятся с помощью заме¬ны переменного к табличным.
Действительно, замечая, что 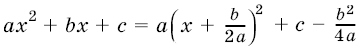 , сделаем замену переменной
, сделаем замену переменной ![]() и положим
и положим 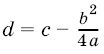 . Тогда
. Тогда 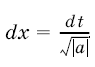 и, в силу формулы (2), получим
и, в силу формулы (2), получим
(перед стоит знак плюс, если а > 0, и знак минус, если а < 0). Интеграл, стоящий в правой части равенства, является табличным. Найдя его по соответствующим формулам и вернувшись от переменной
к переменной
, получим искомый интеграл.
Подобным же приемом вычисляются и интегралы вида
5. Интеграл ![]() можно вычислить с помощью подстановки
можно вычислить с помощью подстановки
. Имеем
, поэтому
Подставляя это выражение и замечая, что
окончательно будем иметь
Заметим, что для проверки результата, полученного при вычислении неопределенного интеграла, достаточно его продифференцировать, после чего должно получиться подынтегральное выражение вычисляемого иптеграла.
Формула замены переменных в определенном интеграле
Теорема.
Пусть функция непрерывна на отрезке
, а функция
имеет непрерывную производную
на отрезке
, причём все значения
при
принадлежат отрезку
, в том числе
и
. Тогда имеет место равенство
Замечание.
Заметим, что доказанная формула, в отличие от формулы замены переменной в неопределённом интеграле, даёт нам возможность после перехода к интегралу от функции новой переменной не возвращаться к исходному интегралу от функции переменной
. После того, как замена сделана, мы можем "забыть", как выглядел исходный интеграл, и продолжать преобразования интеграла от функции новой переменной. Именно на том, что к старой переменной возвращаться не приходится, мы и получаем экономию усилий при применении формулы замены переменной в определённом интеграле, по сравнению с тем, что получилось бы, если бы мы просто нашли первообразную и применили формулу Ньютона - Лейбница.
Обратим ваше внимание на важную особенность формулы: кроме подынтегрального выражения, при замене переменной меняются и пределы интегрирования. Действительно, в интеграле по новой переменной должны быть указаны пределы изменения именно
(то есть
и
), в то время как в исходном интеграле по переменной
указаны пределы изменения
(то есть
и
).
Советы о том, какая замена целесообразна для вычисления того или иного интеграла, - те же самые, что и при вычислении неопределённых интегралов, так что тут ничего нового изучать не придётся.
Пример.
Вычислим интеграл
Для этого сделаем замену , откуда
. Кроме того, при
имеем
, а при
имеем
. Получаем:
Квадратурные формулы интерполяционного типа
Будем рассматривать формулы приближенного вычисления интегралов
где — заданная интегрируемая функция (так называемая весовая функция) и
— достаточно гладкая функция. Рассматриваемые далее формулы имеют вид
где и
— числа,
.
Получим квадратурные формулы путем замены интерполяционным многочленом сразу на всем отрезке
. Полученные таким образом формулы называются квадратурными формулами интерполяционного типа. Как правило, точность этих формул возрастает с увеличением числа узлов интерполирования. Формулы прямоугольников, трапеций и Симпсона являются частными случаями квадратурных формул интерполяционного типа, когда
.
Получим выражения для коэффициентов квадратурных формул интерполяционного типа.
Пусть на отрезке заданы узлы интерполирования
. Предполагается, что среди этих узлов нет совпадающих, в остальном они могут быть расположены как угодно на
.
Заменяя в интеграле (3) функцию интерполяционным многочленом Лагранжа
получим приближенную формулу (4), где
Таким образом, формула (4) является квадратурной формулой интерполяционного типа тогда и только тогда, когда ее коэффициенты вычисляются по правилу (5).
Формула замены переменных в кратном интеграле
Пусть — непрерывно дифференцируемое взаимпо-однозпачное отображение открытого множества
в пространство
и его якобиан
не обращается в нуль на множестве
.
Теорема.
Если — измеримое множество, содержащееся вместе со своим замыканием
в открытом множестве
:
, а функция
непрерывна на множестве
, то
Эта формула равносильна формуле
Действительно, ограниченная функция одновременно интегрируема или нет как на измеримом множестве, так и на его замыкании, причем в случае интегрируемости интегралы от функции по множеству и по его замыканию совпадают.
В нашем случае функции и
![]() непрерывны соответственно на компактах
непрерывны соответственно на компактах и
(являющихся замыканием измеримых множеств
и
), следовательно, ограничены и интегрируемы на них.
Таким образом, все входящие в формулы (6) и (7) интегралы существуют, а сами эти формулы равносильны. Эти формулы называются формулами замены переменных в кратном интеграле.
Замена переменных в кратном интеграле часто существенно упрощает его исследование и вычисление. При этом в отличие от однократного интеграла нередко целью замены переменного является не упрощение подынтегральной функции, а переход к более простой области интегрирования даже ценой некоторого усложнения подынтегральной функции.
В качестве примера применения формулы замены переменных в кратном интеграле рассмотрим для двумерного интеграла случай перехода от декартовых координат к полярным.
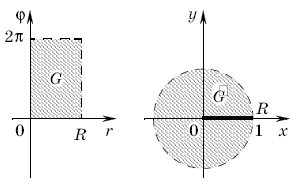
Рассмотрим плоскость, на которой декартовы координаты обозначены ,
и на ней открытый прямоугольник
При отображении
прямоугольник отображается на множество
плоскости с декартовыми координатами
, которое представляет собой круг
![]() , из которого удален радиус
, из которого удален радиус ![]() .
.
Отображение (8) и его якобиан
непрерывно продолжаемы на замкнутый прямоугольник
образом которого при продолженном отображении является замкнутый круг , на котором
отображение (8) уже не является взаимно-однозначным: взаимная однозначность нарушается на границе прямоугольника
— отрезки
![]() при
при и
отображаются в один и тот же отрезок
![]() ,
, , а отрезок
![]() и вовсе отображается в точку (0, 0). Якобиан продолженного отображения обращается в нуль при
и вовсе отображается в точку (0, 0). Якобиан продолженного отображения обращается в нуль при .
Для отображения (8) и непрерывной на круге ![]() функции
функции имеет место формула
Приведем конкретный пример вычисления интеграла по этой формуле:
Сведения об интегралах с бесконечными пределами
Определение.
Пусть функция непрерывна на бесконечном промежутке
. Несобственным интегралом от функции
на промежутке
называется предел
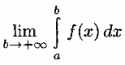 и обозначается
и обозначается
Определение.
Пусть функция непрерывна на бесконечном промежутке
. Несобственным интегралом от функции f(x) на промежутке
называется предел
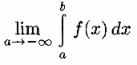 и обозначается
и обозначается
Определение.
Пусть функция непрерывна на всей числовой оси. Несобственный интеграл от функции
на бесконечном промежутке
определяется равенством
где — любое число на оси
.
Из определений следует, что сходящиеся несобственные интегралы с бесконечными пределами интегрирования являются конечными пределами определенных интегралов с переменными верхним или нижним пределами при стремлении этих пределов к бесконечности.
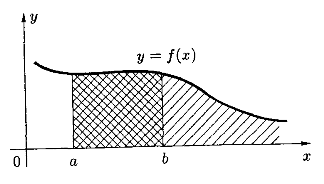
Пусть функция непрерывна и неотрицательна на бесконечном промежутке
. Известно, что интеграл
численно равен площади криволинейной трапеции, ограниченной снизу отрезком
оси
, сверху — кривой
, слева и справа — прямыми
и
. При возрастании
прямая
перемещается вправо вдоль оси
. Если при этом интеграл
сходится, то его величину принимают за площадь бесконечной трапеции, ограниченной снизу осью
, сверху — графиком функции
, слева — прямой
.