EM-алгоритм с последовательным добавлением компонент (пример)

Материал из MachineLearning.

Версия от 18:09, 17 мая 2009; Pavlov99 (Обсуждение | вклад)

(разн.) ← Предыдущая | Текущая версия (разн.) | Следующая → (разн.)

Содержание

1 Постановка задачи
2 Алгоритм отыскания оптимальных параметров
3 Вычислительный эксперимент
4 Исходный код
5 Смотри также
6 Литература
7 Замечания

EM-алгоритм с последовательным добавлением компонент — метод нахождения функции плотности объектов, представляющей смесь распределений. В тех случаях, когда "форму" класса не удаётся описать каким-либо одним распределением, можно попробовать описать её смесью $k$ распределений, каждое из которых описывается функцией правдоподобия $p_j(x)$ .

$p(x) = \sum_{i=1}^k w_jp_j(x)$

$w_j$ - априорная вероятность $j$ -й компоненты. Функции правдоподобия принадлежат параметрическому семейству распределений $\varphi(x; \theta)$ и отличаются только значениями параметра $p_j(x) = \varphi(x; \theta_j)$

Задача разделения смеси заключается в том, чтобы, имея выборку $X^m$ случайных и независимых наблюдений из смеси $p(x)$ , зная число $k$ и функцию $\varphi$ , оценить вектор параметров $\Theta = (w_1,...,w_k,\theta_1,...,\theta_k)$

В данной статье рассматривается смесь гауссовских распределений выборки. Предполагается, что произвольную функцию распределения можно представить в виде их линейной комбинации. Количество компонент смеси, т.е. число гауссианов в линейной комбинации, произвольно.

EM-алгоритм был предложен и исследован М.И.Шлезингером как инструмент для самопроизвольной классификации образов. Область его применения чрезвычайно широка: дискриминантный анализ, кластеризация, восстановление пропусков в данных, обработка сигналов и изображений. Алгоритм решает задачу исключающего или (XOR)

Постановка задачи

Задана выборка $\{(\mathbf{x}_i,y_i)\}_{i=1}^m$ , в которой $X^m$ = $\{\mathbf{x}_i\}_{i=1}^m$ - множество объектов, $Y^m$ = $\{\mathbf{y}_i\}_{i=1}^m$ - множество ответов. Предполагается, что на множестве объектов задана плотность распределения $p(x)$ , представленная в виде смеси $k$ гауссиан с параметрами $\mu$ и $\Sigma$ ,

$p(x) = \sum_{i=1}^k w_jp_j(x) = \sum_{i=1}^k w_jN(x;\mu_j,\Sigma_j).$ $N(x;\mu_j,\Sigma_j) = \frac{1}{\sqrt{(2\pi)^ndet\Sigma_j}}e^{-\frac{1}{2}(x-\mu_j)\Sigma_j^{-1}(x-\mu_j)^{T}}$

Задача разделения смеси заключается в том, чтобы, имея выборку $X^m$ случайных и независимых наблюдений из смеси $p(x)$ оценить вектор параметров $\theta = (w_1,...,w_k,\mu_1,...,\mu_k,\Sigma_1,...,\Sigma_k)$ доставляющий максимум функции правдоподобия

$Q(\Theta) = \ln\prod_{i=1}^mp(x_i|w,\mu,\Sigma) = \sum_{i=1}^m\ln\sum_{j=1}^kw_jp_j(x_i) \rightarrow \max_{\Theta}$

Алгоритм отыскания оптимальных параметров

Оптимальные параметры отыскиваются последовательно с помощью EM-алгоритма. Идея заключается во введении вспомогательного вектора скрытых переменных $G$ , обладающего двумя замечательными свойствами. С одной стороны, он может быть вычислен, если известны значения вектора параметров $\Theta$ , с другой стороны, поиск максимума правдоподобия сильно упрощается, если известны значения скрытых переменных. EM-алгоритм состоит из итерационного повторения двух шагов. На E-шаге вычисляется ожидаемое значение (expectation) вектора скрытых переменных $G$ по текущему приближению вектора параметров $\Theta$ . На М-шаге решается задача максимизации правдоподобия (maximization) и находится следующее приближение вектора $\Theta$ по текущим значениям векторов $G$ и $\Theta$ .

Если число компонент смеси заранее неизвестно, то применяется EM-алгоритм с последовательным добавлением компонент. Предположим, что смесь содержит одну компоненту ( $k=1$ ) и проделаем алгоритм EM( $X,1$ ). Найдем плохо классифицированные элементы: Если функция правдоподобия на объекте меньше своего максимального значения в R раз, то добавим элемент ко множеству U. Параметр R выбирается на основании эвристических соображений, как правило $R \in [2,10]$ . Множество U полагается пустым и увеличивается по мере добавления в него элементов. Если размер U оказался больше $m_0$ , то считаем, что текущее распределение плохо описывает смесь. Текущее распределение определяется только числом компонент $k$ . Увеличим его на единицу и запустим еще раз EM( $X,k+1$ ). Алгоритм остановится, когда число плохо классифицированных объектов будет меньше $m_0$ . Этот параметр характеризует количество элементов, по которому можно восстановить гауссовское распределение. Как правило $m_0 \geq 10$

Вход:

Выборка $X^m = \{x_1,...,x_m\}$ ; $R$ - максимальный допустимый разброс правдоподобия объектов; $m_0$ - минимальная длина выборки, по которой можно восстановить плотность; $\delta$ - параметр критерия останова;

Выход:

$k$ - число компонент смеси; $\Theta = (w_j,\mu_j,\Sigma_j)_{j=1}^k$

Алгоритм

1. начальное приближение - одна компонента:
     $k:=1; \qquad w_1:=1; \qquad \mu_1=\frac{1}{w_1}\sum_{i=1}^m g_{i1}x_i; \qquad \Sigma_1 = \frac{1}{mw_1}\sum_{i=1}^m g_{i1}(x_i-\mu_j)(x_i-\mu_j)^{T};$
2. для всех $k:= 2,3,4...$
3.      выделить объекты с низким правдоподобием
         $U:= \{x_i \in X^m\ | ~ p(x_i) < \frac{max_j ~ p(x_j)}{R} \}$
4.      Если $|U|<m_0$ то выход из цикла по $k$
5.      Начальное приближение для $k$ компоненты:
         $w_k:=\frac{1}{m}|U|; \qquad \mu_k=\frac{1}{mw_k}\sum_{i=1}^m g_{ik}x_i; \qquad \Sigma_k = \frac{1}{mw_k}\sum_{i=1}^m g_{ik}(x_i-\mu_j)(x_i-\mu_j)^{T};$
         $w_j:=w_j(1-w_k) \qquad j = 1,...,k-1;$
6.     $EM(X^m,k,\Theta,\delta);$

Вычислительный эксперимент

Алгоритм тестируется на модельных и реальных данных.

Пример 1

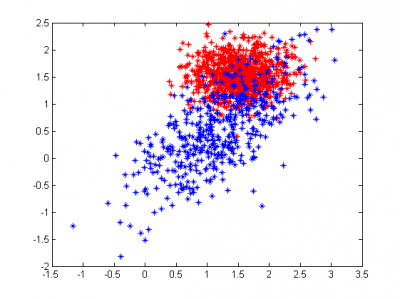
Рассмотрим пример на модельных данных. Выборка состоит из четырех классов. Красный класс представляет собой смесь двух гауссовских распределений с диагональной и недиагональной матрицами ковариации. Остальные классы являются одним гауссовским рапределением. Дисперсия зеленого класса меньше дисперсий остальных, поэтому его элементы находятся ближе к центру. Дисперсия бирюзовых по одной координате больше, чем по другой, в результате чего класс визуально вытянулся. Центры классов располагаются близко, некоторые классы линейно неразделимы.

[X1, Y1] = gengaussdata(150, [0;0], [1/4,1/2]);
[X2, Y2] = gengaussdata(150, [4;0], [1 5/6;5/6 1]);
[X4, Y4] = gengaussdata(120, [2;4], [1/10;1/10]);
[X3, Y3] = gengaussdata(200, [-2,2], [1/3, 1/3]);
[X5, Y5] = gengaussdata(200, [2,2], [1.25, 1/20]);
X=[X1;X2;X3;X4;X5];
%Y are answers (numbers of classes)
Y=[Y1;Y2;Y3+1;Y4+2;Y5+3];
hold off
drawdata(X,Y,'*');
%learning algorithm
[W,M,Sigma,k,Ytheta] = emlearn(X, Y, [2,40,0.001])
 
%testing and geting answers from algorithm
[Yanswer] = emtest(X, M, Sigma, Ytheta);
 
drawdata(X,Yanswer,'o');
 
%printing centers of classes according to algorithm decision
printcenters(M);

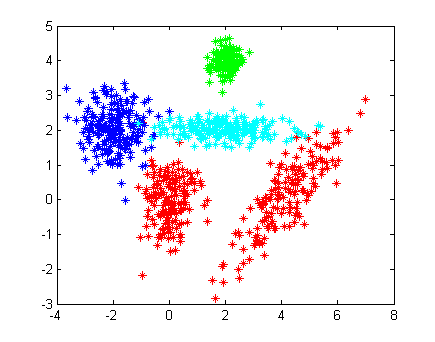
Истинное распределение классов показано на рисунке слева. Одинаковым цветом помечены элементы одного класса. Как можно заметить, некоторые представители "красных", "бирюзовых" и "синих" перемешались.

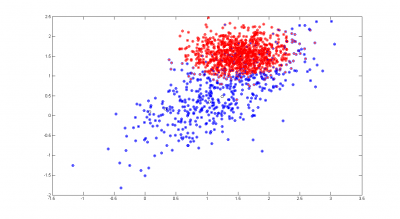
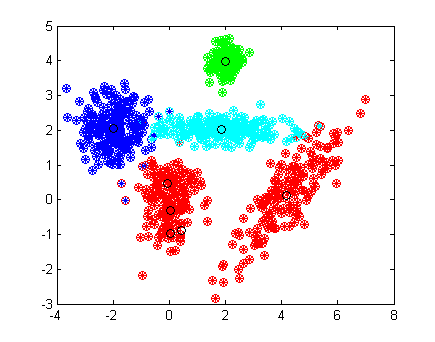
Качество обучения алгоритма проверяется на той же выборке. На правом рисунке кружками показаны полученные ответы, цвет отвечает за принадлежность к соответствующему классу. Центры классов, отмечены черным кружками. Алгоритм нашел восемь гауссовских распределений вместо четырех, причем одна из красных компонент описывается сразу 4 гауссианами, в то время как остальные компоненты выборки - одной. Этот факт говорит о том, что одна гауссиана плохо приближает данное распределение, и, для уменьшения числа ошибок, следует приблизить её большим числом гауссиан. Алгоритм допустил 16 ошибок, что на выборке из 820 элементов составляет менее 2%.

Пример 2

В качестве второго примера возьмем два плохо разделимых класса. Центры классов находятся на расстоянии меньшем дисперсии каждого из них. Можно наблюдать синие элементы, расположенные ближе к центру красного класса, чем к центру своего.

Алгоритм выделил четыре гауссовских распределения в синем классе. Благодаря этому, хорошо классифицировались некоторые синие элементы, находящиеся ближе к красному классу.

Ирисы Фишера

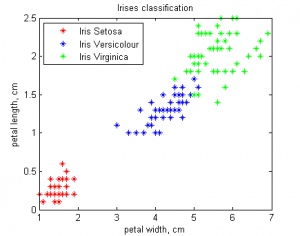
Проверку алгоритма проведем на классической задаче: Ирисы Фишера Объектами являются три типа ирисов: setosa, versicolor, virginica

У каждого объекта есть четыре признака: длина лепестка, ширина лепестка, длина чашелистика, ширина чашелистика. Для удобства визуализации результатов будем использовать первые два признака.

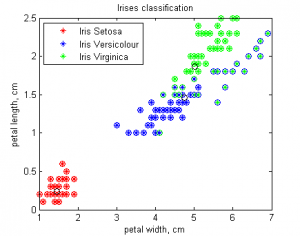
load 'iris2.data'
X = iris2(:,[3,4]);
Y = [ones([50,1]);2*ones([50,1]);3*ones([50,1])];
hold off
drawdata(X,Y,'*');
title('Irises classification')
xlabel('petal width, cm');
ylabel('petal length, cm');
legend('Iris Setosa','Iris Versicolour','Iris Virginica','Location','NorthWest');
[W,M,Sigma,k,Ytheta] = emlearn(X, Y, [2,20,0.0005])
[Yanswer] = emtest(X, M, Sigma, Ytheta);
drawdata(X,Yanswer,'o')

Алгоритм хорошо отделил ирисы setosa от остальных, но допустил 30% ошибок при разделении ирисов versicolor и virginica. Это произошло потому, что алгоритм изначально решал задачу кластеризации и лишь потом задачу классификации, приписывая каждому кластеру номер наиболее хорошо приближаемого им класса. Для разделения последних двух классов можно использовать линейные алгоритмы классификации, либо решать с помощью EM-алгоритма, используя все четыре признака.

Исходный код

Скачать листинги алгоритмов можно здесь EMk.m, emlearn.m, emtest.m

Смотри также

Литература

К. В. Воронцов, Лекции по статистическим (байесовским) алгоритмам классификации
Bishop C. - Pattern Recognition and Machine Learning (Springer, 2006)
The on-line textbook: Information Theory, Inference, and Learning Algorithms, by David J.C. MacKay includes simple examples of the EM-algorithm such as clustering using the soft K-means algorithm, and emphasizes the variational view of the EM-algorithm.
Журавлёв, Юрий Иванович Об алгебраическом подходе к решению задач распознавания или классификации // Проблемы кибернетики. 1978 Т. 33.С. 5–68.
Jordan M. I., Xu L. Convergence results for the EM algorithm to mixtures of experts architectures: Tech. Rep. A.I. Memo No. 1458: MIT, Cambridge, MA, 1993.
Шлезингер М., Главач В. Десять лекций по статистическому и структурному распознаванию. - Киев: Наукова думка, 2004.
Шлезингер М. И. О самопроизвольном различении образов // Читающие автоматы. - Киев, Наукова думка, 1965

Данная статья является непроверенным учебным заданием.

Студент: Участник:Кирилл Павлов

Преподаватель: Участник:В.В.Стрижов

Срок: 28 мая 2009

До указанного срока статья не должна редактироваться другими участниками проекта MachineLearning.ru. По его окончании любой участник вправе исправить данную статью по своему усмотрению и удалить данное предупреждение, выводимое с помощью шаблона {{Задание}}.

См. также методические указания по использованию Ресурса MachineLearning.ru в учебном процессе.

Замечания

Источник — «http://machinelearning.ru/wiki/index.php?title=EM-%D0%B0%D0%BB%D0%B3%D0%BE%D1%80%D0%B8%D1%82%D0%BC_%D1%81_%D0%BF%D0%BE%D1%81%D0%BB%D0%B5%D0%B4%D0%BE%D0%B2%D0%B0%D1%82%D0%B5%D0%BB%D1%8C%D0%BD%D1%8B%D0%BC_%D0%B4%D0%BE%D0%B1%D0%B0%D0%B2%D0%BB%D0%B5%D0%BD%D0%B8%D0%B5%D0%BC_%D0%BA%D0%BE%D0%BC%D0%BF%D0%BE%D0%BD%D0%B5%D0%BD%D1%82_%28%D0%BF%D1%80%D0%B8%D0%BC%D0%B5%D1%80%29»

Категории: Непроверенные учебные задания | Учебные материалы | Классификация | Прикладная статистика