Многомерная интерполяция и аппроксимация на основе теории случайных функций

Материал из MachineLearning.

Содержание 1 Вступление 2 Подход к многомерной интерполяции и аппроксимации на основе теории случайных функций. 2.1 Введение. 2.2 Многомерная интерполяция. 2.3 Дисперсия случайной функции. Множество реализаций, удовлетворяющих узлам интерполяции. 2.4 Многомерная аппроксимация. 2.5 Выводы. 3 Метод машинного обучения. 4 Демонстрация в среде Matlab.

Вступление

(в настоящий момент идет ввод и редактирование статьи, в силу того, что объем довольно значителен а опыта разметки еще нет (прошу прощения за это), сначала планирую выложить описание самого итогового метода, чтобы читатели смогли при желании с ним ознакомиться, затем примеры реализации функций и демонстрации в Matlab, а затем теоретическую часть с обоснованием)

Данную статью условно можно поделить на две части.

• Первая часть посвящена использованию основ теории случайных функций применительно к задачам многомерной интерполяции и аппроксимации, а также машинному обучению и их теоретическому обоснованию. Цель теоретической части показать, что машинное обучение в его парадигме “обучения с учителем”, задачи многомерной интерполяции и аппроксимации, могут быть обобщены на основе теории случайных функций.
  
• Во второй части изложены практические выводы из положений первой части в виде законченного метода машинного обучения (метода многомерной интерполяции и аппроксимации). Если читателя интересуют сугубо практические вопросы, Вы можете перейти сразу к изложению метода.
  
• Предложенный метод позволяет получить точное решение задачи многомерной интерполяции или аппроксимации (“обучение с учителем”) гарантирующее оптимальность (при определенных минимальных допущениях, указанных в теоретической части). Метод достаточно прост и сводится к системе линейных уравнений, что может у читателя не знакомого с вопросом без изучения теоретической части вызвать подозрения в работоспособности или обобщающей способности метода. Но смею Вас уверить, что столь простая математическая конструкция в данном случае никак не ограничивает возможности. Если постараться объяснить кратко, то способности метода обеспечивает “специальная функция”, полученная в теоретической части, применение которой в системе линейных уравнений гарантированно обеспечивает оптимальное, с точки зрения аппарата случайных функций, решение. Использование данной функции позволяет сводить задачи многомерной интерполяции и аппроксимации или самые разнообразные задачи машинного обучения (с определенными допущениями) к решению системы линейных уравнений, гарантируя оптимальность полученного решения, отсутствие переобучения, осцилляций интерполянта и других нежелательных эффектов (если говорить более строго, то в реальных вычислениях используется лишь приближение теоретической “идеальной” функции в используемой части спектра, функция, которую можно записать алгебраически).

Подход к многомерной интерполяции и аппроксимации на основе теории случайных функций.

Введение.

Многомерная интерполяция.

Дисперсия случайной функции. Множество реализаций, удовлетворяющих узлам интерполяции.

Многомерная аппроксимация.

Выводы.

Метод машинного обучения.

Выпишем отдельно ключевые выражения, полученные в теоретической части в виде законченного метода.

• Пусть последовательность представляет собой набор входных векторов для обучения. Пусть соответствующие им представляют собой набор выходных значений. Если значения на выходе представляют собой не один, а набор значений (вектора), то представленные преобразования можно рассмотреть последовательно для каждого из выходных параметров.
  
• Метод позволяет определить функцию, связывающую значения на входе и на выходе (которая будет являться наиболее вероятной реализацией случайной функции, о чем шла речь в теоретической части). Метод также позволяет для произвольного входного значения определить среднеквадратическое отклонение ошибки, которую может дать полученная функция.
  

Функция, связывающая значения обучающей выборки на входе и на выходе будет определяться выражением (103):

Функцию из (103) определим как (104):

где - коэффициенты
- норма (длина) вектора

Коэффициенты для (103) вычисляются из системы линейных уравнений (105):

где - среднеквадратическое отклонение для шума в точке

• Значения определяют априорно предполагаемый уровень шума (погрешности) в данных обучения и соответственно степень приближения, с которой функция (103) воспроизведет данные обучения.
  
• Если , то это будет соответствовать частному случаю, когда погрешность или любая противоречивость в данных отсутствует и, искомая функция должна точно воспроизвести обучающую выборку. Т.е. задача обучения превращается в задачу многомерной интерполяции.
• Если , то это будет соответствовать случаю, когда предполагается что в данных обучения одинаково на всей выборке содержится шум, имеющий нормальное распределение со среднеквадратическим отклонением равным . Задачу обучения можно рассматривать как многомерную аппроксимацию.
  
• Если же уровень шума и его распределение в пространстве обучения неравномерно но известно, его наличие может быть задано в виде функции (или достаточно только ее значений в узлах интерполяции).

Рассмотрим теперь коэффициенты в выражении (104).

• Коэффициенты и в “идеальном случае” должны быть приблизительно равны и устремлены в бесконечность. В реальных вычислениях в качестве этих коэффициентов можно использовать при условии нормирования входных значений в диапазоне [-1,1] (они должны быть на несколько порядков больше диапазона изменения входных значений). С увеличением и разница от использования функции (104) вместо “идеальной функции” устремляется в область все более низких частот (при разложении искомой функции в спектр) измеряемыми и все меньше влияет на результаты обучения в области параметрического пространства, где находится обучающая выборка.
• Коэффициент ,назовем его “калибровочным”, связан со свойствами априорной случайной функции. Хотя непосредственно случайные функции в представленных выражениях (103) - (105) не используются, эти выражения выведены на их основе. (Если и обучение сводится к многомерной интерполяции, значение можно взять произвольным, поскольку при решении системы (105) и вычислении функции (103) он сократится.)

Процедура вычисления (предлагаемый вариант):

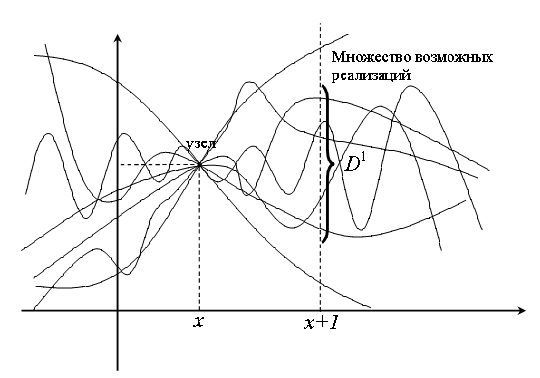
Рис.10. Оценка желаемой дисперсии на единичном расстоянии.

• Калибровка требуется, чтобы найти баланс между возможными погрешностями, неточностями и противоречиями в данных обучения и возможной нелинейностью самой функции, связывающей вход и выход.
• Предположим известно, что искомая функция (103) проходит через некий узел. Для калибровки можно априорно задать желаемый уровень дисперсии множества возможных реализаций на единичном расстоянии от узла. С увеличением при вычислениях (103) – (105) все “ большая роль” будет отводиться возможной нелинейности самой функции, с уменьшением – все больше “списываться” на наличие неточностей в данных обучения. При известном можно вычислить требуемый коэффициент :

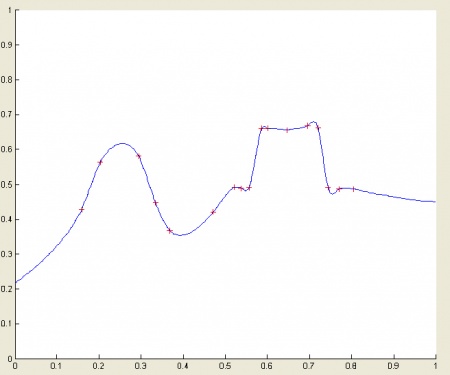
Рис.11. Пример одномерной интерполяции.

• На рис.11. представлен пример одномерной интерполяции (при ). Как видно из рисунка, интерполяция выполнена качественно (отсутствуют осцилляции, которые, например, часто имеют место при использовании интерполяционного многочлена Лагранжа).
• С вводом , интерполяция легко превращается в аппроксимацию - Рис.12.

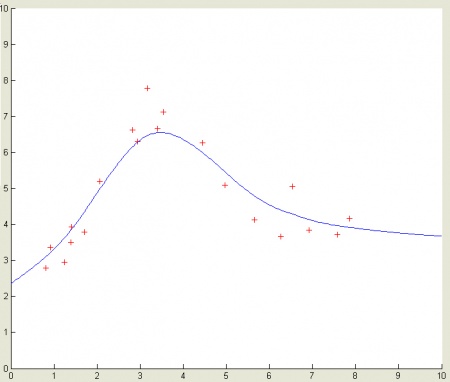
Рис.12. Пример одномерной аппроксимации.

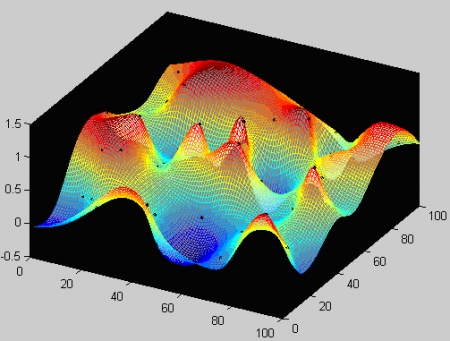
Рис.13. Пример двумерной интерполяции.

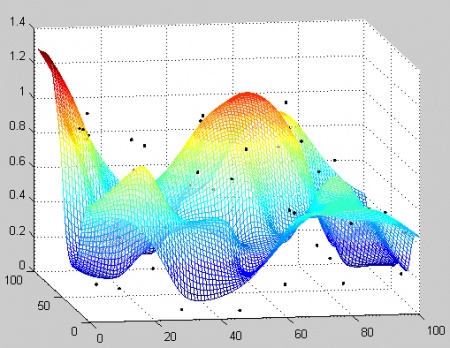
Рис.14. Пример двумерной аппроксимации.

• На Рис. 11 – 14 представлены примеры интерполяции и аппроксимации в одномерном и двумерном случае в целях наглядности результатов. Выражения (103) – (105) могут быть использованы без ограничений для пространства любой размерности.
• Для определения среднеквадратического отклонения возможной ошибки были получены выражения:

• Значение определяется следующим выражением:

• А коэффициенты из (108) находятся решением системы уравнений (109):

• Необходимо отметить, что при расчете среднеквадратического отклонения для каждого значения , необходимо рассчитать индивидуальное значение и заново решать систему уравнений (109) (хотя вычисления можно упростить, единожды вычислив обратную матрицу).
  

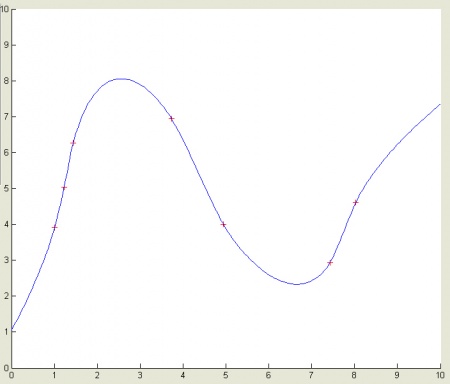
Рис.15. Пример одномерной интерполяции.

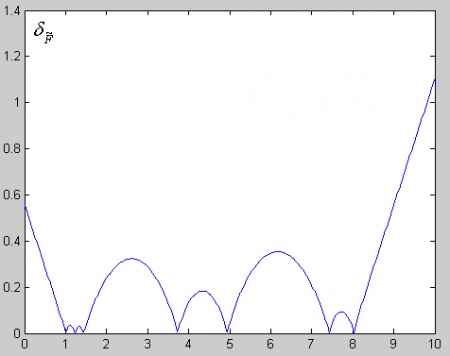
Рис.16. Среднеквадратическое отклонение распределения возможной ошибки как случайной величины для найденной функции на Рис.15

• Ожидаемая ошибка функции (103) как случайная величина (исходя из теоретических положений в первой части) будет иметь нормальное распределение с рассчитанным по (107) среднеквадратическим отклонением и математическим ожиданием равным нулю. Зная это, мы можем ее отобразить графически, как показано на Рис.17.
  

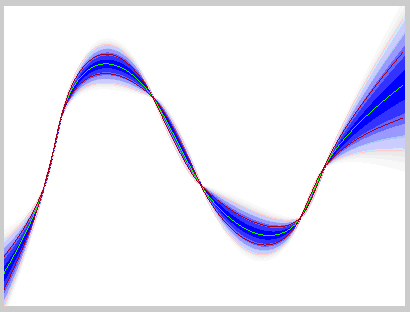
Рис.17. Возможная ожидаемая ошибка, или распределение реализаций случайной функции, удовлетворяющих данным обучения

• С другой стороны, то, что мы можем понимать под возможной ошибкой, представляет собой распределение значений возможных реализаций априорной случайной функции (рассмотренной в теоретической части) которые удовлетворяют данным обучения.
  

Ниже представлены рисунки, демонстрирующие аппроксимацию.

Рис.18. Пример одномерной аппроксимации.

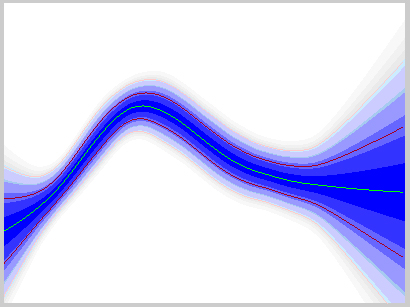
Рис.19. Распределение реализаций или возможная ожидаемая ошибка (для функции на Рис.18).

• Среднеквадратическая ошибка в (107) отражает разброс значений связанный с возможным распределением реализаций. Если требуется учесть возможный шум в самих данных, то для вычисления среднеквадратического отклонения можно воспользоваться выражением:

Демонстрация в среде Matlab.