Многомерная интерполяция и аппроксимация на основе теории случайных функций
Материал из MachineLearning.
Содержание |
Вступление
- Данную статью условно можно поделить на две части.
- Первая часть посвящена использованию основ теории случайных функций применительно к задачам многомерной интерполяции и аппроксимации, а также машинному обучению и их теоретическому обоснованию. Цель теоретической части показать, что машинное обучение в его парадигме “обучения с учителем”, задачи многомерной интерполяции и аппроксимации, могут быть обобщены на основе теории случайных функций.
- Во второй части изложены практические выводы из положений первой части в виде законченного метода машинного обучения (метода многомерной интерполяции и аппроксимации). Если читателя интересуют сугубо практические вопросы, Вы можете перейти сразу к изложению метода.
- Предложенный метод позволяет получить точное решение задачи многомерной интерполяции или аппроксимации (“обучение с учителем”) гарантирующее оптимальность (при определенных минимальных допущениях, указанных в теоретической части). Метод достаточно прост и сводится к системе линейных уравнений, что может у читателя не знакомого с вопросом без изучения теоретической части вызвать подозрения в работоспособности или обобщающей способности метода. Но смею Вас уверить, что столь простая математическая конструкция в данном случае никак не ограничивает возможности. Если постараться объяснить кратко, то способности метода обеспечивает “специальная функция”, полученная в теоретической части, применение которой в системе линейных уравнений гарантированно обеспечивает оптимальное, с точки зрения аппарата случайных функций, решение. Использование данной функции позволяет сводить задачи многомерной интерполяции и аппроксимации или самые разнообразные задачи машинного обучения (с определенными допущениями) к решению системы линейных уравнений, гарантируя оптимальность полученного решения, отсутствие переобучения, осцилляций интерполянта и других нежелательных эффектов (если говорить более строго, то в реальных вычислениях используется лишь приближение теоретической “идеальной” функции в используемой части спектра, функция, которую можно записать алгебраически).
Подход к многомерной интерполяции и аппроксимации на основе теории случайных функций.
Введение.
- Цель данной статьи показать, что машинное обучение в его парадигме “обучения с учителем”, задачи многомерной интерполяции и аппроксимации, могут быть обобщены на основе теории случайных функций.
Использование математического аппарата случайных функций удобно для теоретического обоснования методов машинного обучения, а понятие “вероятность реализации” может служить критерием для обоснования обобщающих способностей метода обучения.
- Ниже будет показано, что использование понятия случайной функции и связанных с ней теоретических построений позволяет получать точные решения задач машинного обучения как задач многомерной интерполяции (или аппроксимации) гарантируя оптимальность решения с точки зрения критерия вероятности. Существует способ при минимальных допущениях получить оптимальное решение задачи машинного обучения путем решения системы линейных уравнений (с доказательством его единственности и оптимальности). Это позволяет получить точное решение, что снимает проблему поиска глобального оптимума и выбора топологии сети, которые имеют место во многих существующих итеративных алгоритмах “обучения с учителем” искусственных нейронных сетей.
Теорией случайных процессов называется математическая наука, изучающая закономерности случайных явлений в динамике их развития. Аналогично тому, как понятие случайного процесса является обобщением понятия случайной величины, случайная функция является обобщением понятия случайного процесса, поскольку функции могут зависеть не от одного, а от нескольких аргументов.
- Реализациями случайной функции являются функции, вид которых она принимает при наблюдении или, например, при проведении опыта. Сама же случайная функция представляет собой множество своих реализаций, с соответствующим распределением вероятностей. Для любой функции, проявления которой мы можем наблюдать, любую функцию которую мы можем в каком-либо смысле рассматривать, всегда можно поставить в соответствие случайную функцию, реализацией которой мы можем ее считать без каких-либо дополнительных предположений или допущений. Даже если мы рассматриваем какую-то конкретную функцию, например, вида y=2x, то и в этом случае мы можем ее считать частным случаем случайной функции, множество реализаций которой состоит из одного элемента с вероятностью реализации равной единице.
При решении задачи многомерной интерполяции или аппроксимации или при машинном обучении по набору примеров требуется связать с помощью некоторой функции значения входных и выходных переменных. Решая подобные задачи, требуется найти нужные функции, удовлетворяющие обучающим векторам, если это машинное обучение, либо узлам интерполяции в случае многомерной интерполяции, притом что таких функций, удовлетворяющих данным, может быть бесконечное множество.
- При создании любого метода решения, выбор всегда будет осуществляться на основе определенных положений. Рассмотрим задачу машинного обучения либо многомерную интерполяцию или аппроксимацию. Предположим, что искомую нами функцию можно рассматривать как реализацию некоторой случайной функции, о которой (о реализации) несет информацию рассматриваемый набор обучающих векторов (либо узлов интерполяции).
При таком подходе естественным критерием для поиска требуемой функции будет вероятность ее как реализации. Поиск нужной функции в этом случае превращается в поиск наиболее вероятной из реализаций случайной функции, которые удовлетворяют обучающим примерам либо узлам интерполяции в случае интерполяции.
- Эта идея является основой предлагаемого на рассмотрение в данной работе метода. Для любой наблюдаемой в окружающем мире функции всегда можно поставить в соответствие случайную функцию, реализацией которой она будет являться, поэтому считая искомую функцию реализацией случайной функции, не уточняя ее характеристик, мы пока еще не делаем никаких дополнительных предположении или допущений, но в то же время можем использовать математический аппарат теории случайных функций.
Адекватность такого подхода, его область применимости, будет целиком определяться тем, какими конкретными характеристиками мы наделим априорную случайную функцию, используя которую мы будем решать ту или иную задачу.
Многомерная интерполяция.
Рассмотрим задачу многомерной интерполяции, предполагая, что узлы интерполяции принадлежат реализации некоторой случайной функции.
- Предположим, что функцию (1) можно считать реализацией некоторой случайной функции
которую можно записать как (2):
где - координатные функции,
- случайные величины,
- функция математического ожидания
- Под координатными функциями в (2) мы можем понимать любые произвольные функции. Условие заключается в том, что существуют какие-то координатные функции, такие, что мы можем через них записать случайную функцию вида (2). Количество слагаемых в (2) может быть произвольным, т.е. полагаем, что m может быть любым, в том числе и равным бесконечности (как вариант, сумма в (2) может быть обобщена до интеграла). В качестве частного случая (2) можно рассматривать, например, разложение в бесконечный ряд синусов и косинусов, когда реализациями данной случайной функции может быть множество всех непрерывных вещественных функций.
- Предполагаем, что в (2) случайные величины
независимы, распределены по нормальному закону, с математическими ожиданиями равными нулю и дисперсией равной единице.
- Потенциально требование именно к нормальному закону на данном необязательно (но может быть спользовано в дальнейшем, например, при анализе и отображении подмножеств реализаций). Для выполнения следующих нескольких преобразований достаточно было бы потребовать, чтобы совместный закон распределения вероятностей для случайных величин из (2) был симметричным относительно начала координат и монотонно убывал с увеличением расстояний от начала координат.
- Требования в (2) для случайных величин к математическому ожиданию равному нулю и дисперсии равной единице сделаны для удобства дальнейших преобразований. Если они не выполняются, можно сделать преобразование, получив снова выражение (2), но чтобы эти требования были выполнены. Предположим, что для какой-либо случайной величины дисперсия не равна единице, тогда мы можем заменить ее и одновременно заменить соответствующую ей координатную функцию (умножив ее на коэффициент), снова получив выражение вида (2). Если же математическое ожидание какой-либо случайной величины в (2) не равно нулю, тогда можно выполнить преобразование, изменив функцию математического ожидания таким образом, чтобы опять свести к виду (2).
- Рассмотрим подробнее функцию
. В частном случае она может быть равна нулю или константе.
- Если эта функция заранее известна, то мы можем исключить ее из дальнейших преобразований, осуществив вычитание ее значений из узлов интерполяции и одновременно удалив из выражения (2). После того как интерполяция по модифицированным узлам будет выполнена мы можем снова прибавить ее к полученному решению для получения окончательного результата.
- Если эта функция заранее не известна, тогда мы можем принять ее за некую реализацию еще одной случайной функции которую можно снова выразить через выражение (2), и дальше повторять эту процедуру в случае необходимости.
Исключив функцию математического ожидания, получим выражение случайной функции:
- Обозначим через
конкретные значения случайных величин из (3), которые они приняли для какой-либо реализации. Тогда плотность распределения вероятностей реализаций в пространстве параметров
(т.е. вероятность реализации случайной функции вида (3), когда случайные величины
принимают некие конкретные значения
) запишется в виде (4):
Пусть последовательности
представляют собой координаты и соответствующие им значения узлов интерполяции.
- Считая, что узлы интерполяции принадлежат одной из реализаций случайной функции (3), которой соответствует вектор
, их можно выразить в виде системы уравнений (6):
- Используя приведенные выше выражения, можно сказать, что наиболее вероятной реализацией случайной функции вида (3) соответствующей узлам интерполяции будет та, при которой функция плотности вероятности (4) принимает максимальное значение с учетом системы ограничений в виде равенств (6).
Поиск максимума функции (4), равносилен поиску минимума функции (7):
- Отсюда можно сделать вывод, что решение задачи многомерной интерполяции как поиск наиболее вероятной реализации функции (2) или (3) удовлетворяющей узлам интерполяции, сводится к задаче квадратичного программирования с ограничениями в виде равенств.
Для поиска минимума (7) при системе ограничений (6), воспользуемся методом множителей Лагранжа.
- Найдем Функцию Лагранжа:
Обозначим вектором решение задачи.
Из условия опять получим уравнения (6).
Из условия получим:
Обозначим последовательности значений координатных функций как вектора
.
Введем коэффициенты обозначив
.
Тогда (9) можно записать через новые обозначения в виде линейной комбинации векторов (10):
- Выражение (10) можно интерпретировать с геометрической точки зрения. Поиск минимума функции (7), с системой ограничений (6), равносилен опусканию перпендикуляра из начала координат на гиперплоскость, образуемую пересечением гиперплоскостей, заданных в виде уравнений (6) (подставив в (6) значения координатных функций, мы можем понимать их как задание гиперплоскостей и их пересечения в n-мерном пространстве), следовательно,
будет являться линейной комбинацией их перпендикуляров.
Систему ограничений (6) можно записать через скалярные произведения векторов (11):
Заменив изпользуя (10) получаем систему уравнений:
Обозначим как вектор последовательность значений
.
Тогда наиболее вероятную реализацию случайной функции (3) можно выразить как выражение (13):
Рассмотрим более подробно скалярное произведение :
что является не чем иным как каноническим разложением корреляционной функции.
Тогда систему уравнений (12) можно записать в виде (15):
а выражение (13), для наиболее вероятной реализации, в виде (16):
- Таким образом, можно сделать вывод, что наиболее вероятной реализацией случайной функции (3), удовлетворяющей узлам интерполяции, будет линейная комбинация сечений ее корреляционных функций.
- Следовательно, зная корреляционную функцию и решив систему уравнений (15), мы получим наиболее вероятную реализацию (16) в рамках данной случайной функции.
- Если же теперь рассмотреть интерполяцию как вариант метода машинного обучения то полученный результат можно легко обобщить на вариант с несколькими выходами, поскольку левая часть уравнений (15) для разных выходных переменных будет одинаковой (если конечно зависимость между входами и разными выходами можно рассматривать, пользуясь одной случайной функцией). В этом случае можно вычислить единую обратную матрицу уравнений (15), которую можно использовать для интерполяции при любых возможных вариантах значений выходных переменных.
- Однако чтобы осуществить подобные расчеты, необходимо знать, какой корреляционной функцией пользоваться (или знать все координатные функции, что будет достаточно для вычисления корреляционной функции), а также знать функцию математического ожидания в (2) либо корректно преобразовать в (3).
Рассмотрим случай, когда нет априорной информации о том, в рамках какой случайной функции можно решать задачу интерполяции. Устранение неопределенности осуществляется выбором корреляционной функции, сделав определенные предположения.
- Предположим, что изначально потенциальными вариантами интерполянта (искомой функции) могут быть любые непрерывные вещественные функции и об их априорном распределении вероятностей между собой не известно. Предположим, что в этом случае, априорно любые точки, а также направления в пространстве интерполяции равнозначны между собой. Поэтому потребуем, чтобы интерполяция не зависела от выбора системы отсчета узлов интерполяции, от операций ее поворота, положения начала координат и масштаба. Т.е. если мы в пространстве интерполяции введем новую систему отсчета (оси координат, путем операций поворота и сдвига исходных), найдем координаты узлов интерполяции в этой новой системе отсчета и выполним интерполяцию, то полученная функция, при переводе ее в исходную систему отсчета должна совпасть с функцией, полученной по исходным узлам. Потребуем выполнения того же свойства и при переходе к новой системе отсчета путем одновременного изменения масштаба по всем координатам (умножив на единый коэффициент значения всех входных и выходных переменных).
- Эти требования можно обеспечить, введя набор положений об априорных вероятностях существования той или иной реализации рассматриваемой случайной функции. Примем априорно равновероятными реализации преобразующиеся друг в друга с помощью операций сдвига поворота или являющиеся подобными друг другу при изменении масштаба. Это допущение обеспечивает выполнение свойств интерполяции при переходе к другой системе отсчета (описанные выше). Действительно, если это допущение выполняется, то при переходе к другой системе отсчета (любым описанным выше способом) появляется возможность отобразить множество реализаций на самого себя таким образом, что мы получим эквивалентную задачу.
- Обозначенных выше требований, не смотря на то, что они и так выглядят естественными в условиях априорной неопределенности, достаточно, чтобы однозначно вычислить корреляционную функцию, необходимую для выражений (15) и (16).
Обозначим сформулированные требования в виде набора положений:
1. Плотность вероятности реализаций, преобразующихся друг в друга параллельным переносом системы координат должна быть одинаковой. Предположим, что мы имеем две реализации и
такие, что:
Тогда плотность вероятности реализаций и
должна быть равна.
2. Плотность вероятности реализаций, преобразующихся друг в друга одинаковым изменением масштаба по всем направлениям должна быть одинаковой. Предположим, что мы имеем две реализации и
такие, что:
где - некоторый коэффициент
Тогда плотность вероятности реализаций и
должна быть равна.
3. Плотность вероятности реализаций, преобразующихся друг в друга поворотом системы координат должна быть одинаковой. Предположим, что мы имеем две реализации и
такие, что:
где - некоторая матрица поворота
Тогда плотность вероятности реализаций и
должна быть равна.
- Выполнение первого пункта означает, что случайная функция будет стационарной. В этом случае ее можно записать в виде многомерного спектрального разложения. Обозначим
ее спектральную плотность (неотрицательная вещественная функция, симметричная относительно любых частот
и
).
- их скалярное произведение
- В выражении (20)
- реализация комплексной случайной функции, каждое значение которой является независимой случайной величиной (кроме дополнительного условия, о котором ниже) имеющей нормальное распределение, единичную дисперсию и математическое ожидание равное нулю, как для вещественной, так и мнимой части. Выражение (20) можно считать частным случаем (3), в котором
, роль координатных функций выполняет
, а аналогом значений случайных величин выступает
. Функцию можно считать разложением реализации по базису функций пропорциональному
.
- Наложим дополнительное условие на
(а соответственно, на случайную функцию), поскольку мы рассматриваем в данный момент интерполяцию вещественных функций, то ее значения для любых значений частот
и
должны быть комплексно-сопряженными. Чтобы отразить это условие поделим пространство частот
на две части
и
. Осуществить это разделение нужно таким образом, чтобы любые частоты
и
лежали разных частях (например, любой гиперплоскостью, проходящей через начало координат). Тогда
можно записать как:
- Где
и
можно рассматривать как реализации вещественных случайных функций, каждое значение которых одинаково для частот
и
, является независимой случайной величиной, имеющей нормальное распределение, математическое ожидание равное нулю и дисперсию равную единице.
При выполнении условия на вещественность реализаций случайную функцию (20) можно записать как (22):
Поскольку и
симметричны относительно
и
, то во втором интеграле в (22) можно перейти к области интегрирования
заменив знак перед частотой. В этом случае получим:
Выполнив далее преобразования, получим:
- Поскольку каждое значение
(для пар частот
и
) является независимой комплексной случайной величиной, с математическим ожиданием равным нулю и дисперсией равной единице, мы можем получить (25) - аналог выражения (7), минимизация которого при выполнении ограничений на узлы интерполяции обеспечит наиболее вероятную реализацию.
Для двух любых реализаций, имеющих одинаковую априорную вероятность значение (25) должно иметь одинаковое значение.
Выражение (25) можно записать как (26):
Пусть последовательность и соответствующие им
- представляют собой узлы интерполяции. Тогда используя полученное выражение (24) ограничения на эти узлы будут представлять собой систему уравнений:
Поиск наиболее вероятной реализации будет соответствовать нахождению функций и
таких, при которых выполняются условия (27) и минимизируется значение выражения (26).
- Дальнейшие рассуждения можно выполнить аналогично (8) – (16).
- Функция Лагранжа примет вид:
При дифференцировании (28) по можно снова получить систему (27).
Поскольку любое значение функций и
для произвольного
выражения (28) можно считать независимой переменной, то соответственно по каждому из них можно выполнить независимое дифференцирование. В этом случае получим выражения:
Подставив решения (29) и (30) в систему (24) получим выражение наиболее вероятной реализации:
Выражение (31) преобразуется в (32):
Поскольку подынтегральное выражение в (32) инвариантно к изменению на
, то мы можем перейти целиком в область интегрирования
:
Введем коэффициенты:
Выражение для корреляционной функции (на самом деле, из-за введенных коэффициентов, это будет функция пропорциональная корреляционной):
Как видно из (35) спектральная плотность случайной функции играет роль спектра для ее корреляционной функции. Сама же корреляционная функция превращается в автокорреляционную, что и следовало ожидать из условия стационарности:
- Отсутствие в (35 - 36) синусной составляющей, говорит о том, что автокорреляционная функция должна быть симметрична относительно нуля, что можно было ожидать. Соответственно в случае, если спектральная плотность случайной функции будет известна, появляется потенциальная возможность вычислить автокорреляционную функцию.
Тогда наиболее вероятную реализацию можно выразить:
Найдем систему уравнений для вычисления коэффициентов в (37). Подставив (29) и (30) в (27) получим:
Используя (34) и (36) в (38) получим систему уравнений для вычисления коэффициентов для (37) (аналог (15)):
- Таким образом, мы получили выражения (37) и (39) - аналоги выражение (15) и (16), а также выражение (36) для корреляционной функции. Для раскрытия неопределенности остается определить спектральную плотность
случайной функции.
- Обозначим как
спектральное разложение Фурье реализаций рассматриваемой нами случайной функции. Из выражения (20) - спектрального разложения случайной функции видно, что спектр реализаций будет равен:
- Теперь вернемся ко второму пункту (выражение (18)).
Обозначим за спектр некоторой функции
, а
- спектр некоторой функции
.
Будем считать, что
т.е. функции подобны, но совпадают в масштабе k:1.
Поскольку
- их скалярное произведение
Получим
Откуда можно вывести соотношение спектров подобных функций:
Для обеих рассмотренных функций значение выражения (25) должно быть одинаковым.
Функцию для (25) можно выразить через спектры реализаций и спектральную плотность случайной функции:
Приравнивая выражение (25) для двух рассмотренных выше реализаций (причем, поскольку под знаком интегрирования берется значение по модулю, мы можем интегрировать по ), а также используя выражения (44) и (45) получаем:
Из выражения (46), сравнивая начало и конец полученных равенств можно получить соотношение для спектральной плотности:
Чтобы выполнялось третье положение (19), автокорреляционная функция должна обладать радиальной симметрией. Соответственно радиальной симметрией должна обладать и спектральная плотность. Тогда из (47) можно получить выражение для спектральной плотности:
где - некоторый коэффициент
или(то же самое):
- Таким образом, в выражении (48-49) мы получили искомую спектральную плотность случайной функции. При использовании корреляционной функции с таким спектром и решении системы линейных уравнений (39) будет гарантированно получена наиболее вероятная реализация случайной функции (если брать в качестве основы положения (17) – (19)).
- Коэффициент
в (48) – (49) может быть любым, поскольку его изменение одновременно увеличит или уменьшит все коэффициенты левой части системы уравнений (39) и в уравнении (37) в одинаковое количество раз, а соответственно и коэффициенты решения, которые при подстановке в (37) дадут ту же самую функцию.
- Для непосредственно вычисления выражения функции со спектром (49) можно воспользоваться свойством симметричности функции. В этом случае для упрощения можно сначала рассмотреть одномерный вариант, после чего получить многомерный вариант, воспользовавшись требованием симметричности.
В одномерном случае требуемая спектральная плотность будет:
Тогда выражение для автокорреляционной функции (36) в одномерном случае примет вид:
Выражение (51) можно записать как:
Последовательно интегрируя по частям, получим:
В качестве последнего правого слагаемого в (53) был получен интегральный косинус. Рассмотрим его более подробно:
Интегральный косинус может быть раскрыт:
где - постоянная Эйлера
Используя (53) и (55) получим:
Таким образом, получаем результат:
- Хотя в реальных вычислениях невозможно использовать
, можно взять ее значение сколь угодно близкое к нулю, тем самым приблизив ее спектр к выражению (50). Для вычислений вместо (57) может быть использован более упрощенный вариант (58).
- Учитывая, что коэффициент
в (48)-(49) можно взять любым (возьмем равным 0.5), а также воспользовавшись свойством симметричности, получаем вариант функции для многомерного случая:
где - норма ветора,
Выпишем еще раз выражения (39) и (37):
- Таким образом, в виде (58)-(60) получаем итоговые выражения метода многомерной интерполяции. Метод в пределе функции (58) обеспечивает поиск наиболее вероятной реализации случайной функции, удовлетворяющей положениям (17)-(19) об инвариантности преобразований систем отсчета.
- При реальных расчетах (как показали вычислительные эксперименты) в качестве
и
можно брать числа примерно одного порядка и на много порядков больше диапазона изменения
. Ниже еще вернемся к этому вопросу.
- Как видно из рисунка, использование функции (58) позволяет производить качественную интерполяцию нелинейных функций с помощью обычной системы линейных уравнений, что и следует из теории.
Дисперсия случайной функции. Множество реализаций, удовлетворяющих узлам интерполяции.
- В рассмотренном выше случае под решением задачи интерполяции (58-60) подразумевался поиск наиболее вероятной реализации случайной функции, удовлетворяющей узлам интерполяции. Однако целиком множество реализаций, удовлетворяющих узлам интерполяции, кроме некоторых частных случаев выражения (3), бесконечно. Было бы полезно иметь характеристики этого множества, кроме того, они необходимы, чтобы перейти от задачи многомерной интерполяции к задаче аппроксимации (как алгоритма полноценного машинного обучения).
- Выразим дисперсию случайной функции (3) для некоторой произвольной точки
, зная, что дисперсии всех случайных величин из (3) равны единице:
- Как видно из (60) дисперсия случайной функции (3) в точке
равна значению ее корреляционной функции от двух одинаковых значений этой точки. Для случайной функции с автокорреляционной функцией (51), (57) либо (58) дисперсия будет одинаковой во всех точках и равна их значению от нуля. Для (58) значение дисперсии будет равно
:
- Поскольку в (58) значение
устремлено в бесконечность то в пределе и дисперсия такой случайной функции будет равна бесконечности.
Рассмотрим, чем будет являться значение реализации случайной функции (3) для некого конкретного значения .
- Обозначим как
вектор значений
.
- Обознаяим как
вектор
случайных величин из (3).
Тогда:
Значение случайной функции (3) или (63) для некого конкретного значения будет являться случайной величиной распределенной по нормальному закону с дисперсией определяемой формулами (61- 62).
- Пусть последовательность
и соответствующие им
- представляют собой узлы интерполяции.
- Обозначим векторами
последовательности значений
- Тогда вектор
можно будет представить как сумму двух перпендикулярных векторов:
где
Причем потребуем, чтобы вектор был перпендикулярен любому из векторов
. Тогда разложение (64) для каждого конкретного
будет индивидуальным и единственным. Коэффициенты
в (65) всегда можно подобрать таким образом, чтобы получить разложение (64), поскольку при таком разложении (64-65) количество уравнений равно количеству неизвестных. Вектор
, по сути, является проекцией вектора
на гиперплоскость, образуемой базисом из векторов
, а вектор
является оставшейся его частью, перпендикулярной данной гиперплоскости.
- Тогда (63) можно записать как:
Из (66) видно, что при таком представлении случайную величину можно считать суммой двух случайных величин
и
, причем они будут независимые. Докажем это.
- Любой набор случайных значений вектора
также можно разложить на два перпендикулярных вектора:
где
Также потребуем, чтобы вектор был перпендикулярен любому из векторов
. Тогда получим:
Часть слагаемых из (69) сократятся, в силу того, что скалярное произведение перпендикулярных векторов равно нулю.
- Коэффициенты
из (68) являются коэффициентами
из (10) или (15).
- Вектора
и
являются перпендикулярными и образуют в сумме вектор
, имеющий многомерный нормальный закон распределения. Следовательно, в силу свойств нормального закона распределения мы можем рассматривать (66) как разложение исходной случайной функции на сумму
и
двух независимых случайных функций.
- Рассмотрим
:
Что при известных значениях в узлах интерполяции автоматически превращается в наиболее вероятную реализацию, вычисляемую через формулы (15) и (16).
- Таким образом, случайную функцию (3) при известных координатах узлов интерполяции можно представить как сумму двух независимых случайных функций.
- случайную функцию, реализациями которых являются функции, вычисляемые через (15) и (16) как наиболее вероятные реализации исходной случайной функции (3) и
- случайную функцию, представляющую собой разность (“ошибку”) между найденной наиболее вероятной реализацией и настоящей реализацией случайной функции о которой нам не известно.
- Если рассматривать
как случайную величину в конкретной точке
то она будет распределена по нормальному закону с математическим ожиданием равным нулю.
- Следует отметить тот факт, что поскольку разложение (64)-(65) не зависит от конкретных значений в узлах интерполяции то и функция
, а соответственно и вероятность ошибки интерполяции при любом конкретном
не будет зависеть от значений в узлах интерполяции, а только от расположения координат самих узлов.
Предположим, что известны значения искомой функции в узлах интерполяции. Тогда выражение (66) обратится в следующий вид (введем новое обозначение):
где - наиболее вероятная реализация, вычисленная в (15)-(16)
- Выражение (73) можно понимать как случайную функцию выражающую целиком множество реализаций удовлетворяющих узлам интерполяции (с соответствующим распределением вероятностей между ними).
Дисперсию (61) случайной функции используя (69) можно записать:
Дисперсия случайной функции (73) будет равна:
Рассмотрим , где
- координата одного из узлов интерполяции.
Получаем систему уравнений:
Выразим дисперсию :
Повторим еще раз функцию (58):
где - норма ветора,
Если использовать полученную автокорреляционную функцию (58) то получим систему уравнений:
Как видно из (79) получилась система уравнений, левая часть которой совпадает с (59), но в правой части вместо значений в узлах интерполяции находятся значения автокорреляционной функции.
Выражение дисперсии :
Тогда дисперсия множества реализаций, удовлетворяющих узлам:
- Если рассматривать множество реализаций, удовлетворяющих узлам интерполяции с соответствующим им распределением как новую случайную функцию, то среднеквадратическое отклонение такой функции будет:
- Как уже отмечалось ранее, умножение корреляционной или автокорреляционной функции в уравнениях (15) - (16) или (58) – (60) на любой конечный ненулевой коэффициент и использование такой новой функции не изменит найденную в этих уравнениях наиболее вероятную реализацию.
- Однако при работе с дисперсией значение автокорреляционной функции в нуле будет напрямую влиять на ее значение. Кроме того, как будет видно ниже, это влияет на результаты при переходе к задаче многомерной аппроксимации.
- Поскольку умножение автокорреляционной функции на конечный ненулевой коэффициент не влияет на результаты интерполяции, можно выполнить “калибровку” дисперсии автокорреляционной функции в соответствии с априорными предпочтениями (которые могут следовать из условий решаемой задачи).
- Осуществить калибровку можно различными способами. Ниже предложен один из вариантов.
- Калибровку можно осуществить оценкой на основе априорных предпочтений и заданием коэффициента перед автокорреляционной функцией.
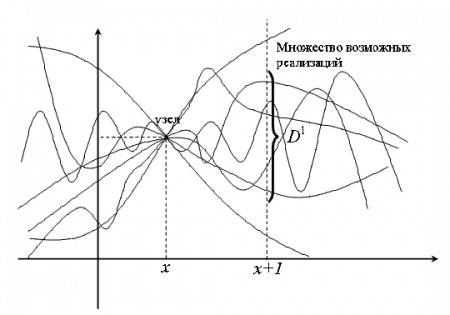
Рис.2. Априорная оценка дисперсии на единичном расстоянии от узла интерполяции.
- Предположим известно значение реализации случайной функции в одном узле интерполяции (Рис.2.). Если существует возможность каким-либо образом оценить или сделать предположение о величине дисперсии разброса реализаций на единичном расстоянии от него, тогда можно выполнить калибровку.
- Допустим, что мы хотим, чтобы используемая нами априорная случайная функция обладала такими свойствами, чтобы на единичном расстоянии от известного узла дисперсия разброса реализаций, удовлетворяющих узлу, равнялась некоторому желаемому значению
.
- Предположим, что используется функция (58) с заданными значениями
и
, используемыми в реальных вычислениях. Введем калибровочный коэффициент:
где - калибровочный коэффициент
Вычислим значение калибровочного коэффициента при заданных и
такое, чтобы дисперсия на единичном расстоянии от узла равнялась желаемому значению
.
Из (79) получим:
Подставим (83) в (84):
Выразим :
Тогда:
Выразим желаемую дисперсию на единичном расстоянии:
Выполнив преобразования, получим:
Откуда можно вычислить коэффициент калибровки:
Пример:
Рассмотрим случай одномерной интерполяции. Пусть область интерполяции находится в диапазоне от 0 до 10. Будем использовать следующие значения для функции (83): .
- Вычислим калибровочный коэффициент:
- На Рис.3. представлен пример одномерной интерполяции, полученный с использованием функции (83) и уравнений (59) – (60). Однако, как уже было сказано выше, калибровочный коэффициент
не влияет на результат интерполяции (на вычисление наиболее вероятной реализации).
- Найдем среднеквадратическое отклонение случайной функции, представляющей собой подмножество реализаций априорной случайной функции удовлетворяющих узлам интерполяции (выражения (79) – (82)). Результат представлен на Рис.4.
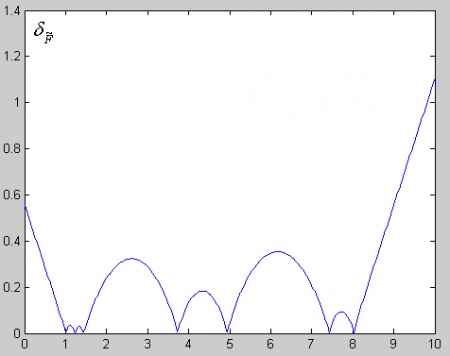
Рис.4. Среднеквадратическое отклонение множества реализаций, удовлетворяющих узлам интерполяции.
- Случайная функция (73) для произвольного
представляет собой случайную величину, имеющую нормальное распределение. При известном среднеквадратическом отклонении мы можем отобразить полученное множество реализаций графически (Рис.5).
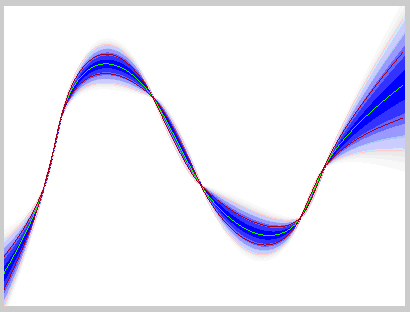
Рис.5. Графическое отображение множества реализаций, удовлетворяющих узлам интерполяции. Интенсивностью синего цвета символизируется вероятность прохождения реализации через данные точки.
- Как видно из Рис.4. среднеквадратическое отклонение в узлах интерполяции равно нулю, что соответствует ожиданиям, поскольку значения искомой функции в этих узлах известны и соответственно никакой неопределенности быть не может.
- Выше был представлен пример одномерной интерполяции и вычисления для данного частного случая среднеквадратического отклонения по оставшемуся множеству реализаций, удовлетворяющих узлам. Был рассмотрен одномерный случай в силу наглядности его графического отображения. Для представленных преобразований нет ограничения по размерности пространства интерполяции.
- Если рассматривать подобную интерполяцию как метод машинного обучения, то вычисление среднеквадратического отклонения
может позволить не только вычислять значения выходных переменных но и оценить их надежность, возможный разброс их значений.
- Несмотря на то, что вычислительные эксперименты убедительно подтверждают работоспособность метода при использовании
(при области интерполяции измеряемой единицами), остается открытым вопрос о влиянии их значений на погрешность интерполяции по сравнению с рассчитанной “идеальной функцией” (57) – (58).
- Очевидно, что такая погрешность связана с отклонением спектра используемой автокорреляционной функции от эталонного спектра (49) –(50), что также может привести к искажению полученного интерполянта в этой же частотной области. Анализируя выражение (52) – поскольку при конечных коэффициентах в (58),
в (52) не достигает нуля, можно сделать вывод, что главные искажения сведутся в низкочастотную область в пределах
или
, что при
и области интерполяции [0,10] не должно значительно сказываться на результатах.
- Однако вопрос о погрешности остается открытым, чему планируется в дальнейшем посвятить отдельную исследовательскую работу.
Многомерная аппроксимация.
- При решении задачи многомерной интерполяции предполагалось, что искомая реализация должна точно соответствовать узлам интерполяции. Если переводить в термины машинного обучения, был рассмотрен вариант такого обучения, когда ошибка обучения должна быть равна нулю. Во многих случаях точно воспроизводить обучающую выборку не требуется или это может вредно сказаться на качестве обобщающих способностей. Данные могут быть не точными, содержать погрешности или даже быть противоречивыми. Т.е. требуется решение задачи не интерполяции, а аппроксимации многомерных данных.
- Перейти к задаче аппроксимации можно предположив, что значения улов интерполяции могут не соответствовать породившей их реализации и могут отличаться от ее значений на некоторую случайную величину.
- Пусть последовательность
и соответствующие им
- представляют собой узлы интерполяции. Предположим, что координаты узлов
представляют собой комплексные числа, к которым были прибавлены бесконечно малые мнимые части, такие, что теперь координаты узлов не могут быть точно равны не между собой, ни какому либо другому вещественному числу.
- В этом случае выражение (3) мы можем модифицировать следующим образом:
- обновленные координаты узлов интерполяции
- В выражении (91) были добавлены дополнительные случайные величины, а также набор функций
, которые принимают значение равное
в соответствующих им узлах интерполяции и имеющие нулевое значение во всех остальных точках.
- Поскольку значения узлов интерполяции не могут точно равняться друг другу, ни какому либо другому вещественному значению, функции
принимают ненулевое значение исключительно для соответствующих узлов и, выражения (91) и (92) полностью имитируют наличие погрешностей в значениях узлов интерполяции. Использование такой случайной функции (91) будет эквивалентно наличию в значениях узлов интерполяции шума, с нормальным распределением и среднеквадратическим отклонением равным
. В то же время мы можем использовать функции
как полноценные дополнительные координатные функции в выражении (3).
- Приняв
как дополнительные координатные функции в (3) можно выполнить без изменений все преобразования (3) – (16). Изменения коснутся лишь корреляционной функции, обозначим ее как
:
- некоторые произвольные значения
- Тогда корреляционную функцию в
- узлах интерполяции можно выразить как:
- Для произвольных вещественных значений
корреляционная функция останется неизменной (14).
- Используя (94) получим, что учет существования шума в значениях узлов интерполяции с нормальным законом распределения и среднеквадратическим отклонением равным
эквивалентен добавлению в уравнение (15) к главной диагонали значений
(дисперсию шума).
- Для автокорреляционной функции (58) или (83) получаем систему уравнений:
- Уравнение для наиболее вероятной реализации остается неизменным:
Пример аппроксимации:
Графическое отображение множества реализаций, соответствующее аппроксимации представлено на Рис.7.
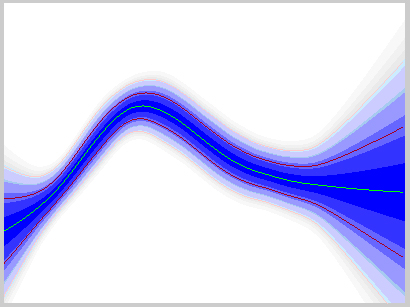
Рис.7. Пример отображения множества реализаций при аппроксимации.
Поскольку мы ввели учет шума с помощью дополнительных координатных функций то все рассуждения, касающиеся дисперсии случайной функции (61) – (62) остаются в силе. Изменения коснутся только системы уравнений (79), которую теперь можно представить как (98):
- Следует отметить, что в результате вычисления среднеквадратического отклонения реализаций, удовлетворяющих узлам (отображенное на рис.7) – его значение отражает лишь распределение порождающих реализаций случайной функции без учета возможных погрешностей в их значениях.
- В выражении (92) функции
принимают значение равное
либо нулевое значение. Однако если известно распределение шума в области аппроксимации, это распределение можно непосредственно учесть в выражении (92), поскольку для каждого узла может быть задано индивидуальное значение среднеквадратического отклонения шума:
где - значение среднеквадратического отклонения шума в
Тогда выражение (96) примет вид:
где
А выражение (98) будет:
- Пример. Рассмотрим одномерный случай.
Предположим, распределение шума (его среднеквадратического отклонения) в области аппроксимации определяется выражением:
Т.е. в области около нуля шум почти отсутствует и возрастает по мере удаления.
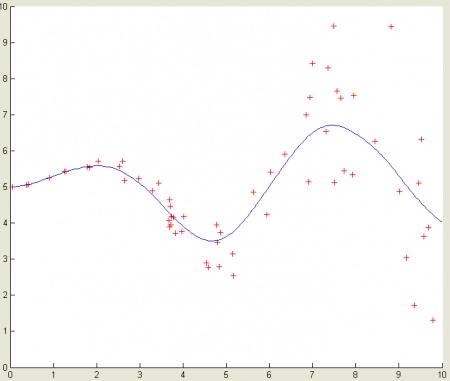
Рис.8. Аппроксимация с учетом распределения шума.
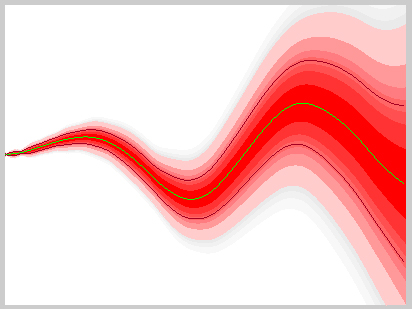
Рис.9. Графическое отображение множества реализаций.
- На рис.8. представлена аппроксимация с использованием системы уравнений (100) и выражением для среднеквадратического значения в распределении шума (102).
- На рис.9. для более наглядного сравнения с рис.8. множество реализаций отображено с учетом шума (102).
Выводы.
- Проведенные рассуждения и преобразования показывают, что интерполяция и аппроксимация могут быть обобщены на основе теории случайных функций как поиск наиболее вероятных реализаций, удовлетворяющих информации об узлах. В результате был получен метод, которые можно рассматривать как метод “машинного обучения”, имеющий точное решение, обеспечивающий получение оптимального результата по критерию вероятности, при соблюдении введенных условий по преобразованию систем отсчета.
Метод машинного обучения.
Выпишем отдельно ключевые выражения, полученные в теоретической части в виде законченного метода.
- Пусть последовательность
представляет собой набор входных векторов для обучения. Пусть соответствующие им
представляют собой набор выходных значений. Если значения на выходе представляют собой не один, а набор значений (вектора), то представленные преобразования можно рассмотреть последовательно для каждого из выходных параметров.
- Метод позволяет определить функцию, связывающую значения на входе и на выходе (которая будет являться наиболее вероятной реализацией случайной функции, о чем шла речь в теоретической части). Метод также позволяет для произвольного входного значения определить среднеквадратическое отклонение ошибки, которую может дать полученная функция.
Функция, связывающая значения обучающей выборки на входе и на выходе будет определяться выражением (103):
Функцию из (103) определим как (104):
где - коэффициенты
- норма (длина) вектора
Коэффициенты для (103) вычисляются из системы линейных уравнений (105):
где
- Значения
определяют априорно предполагаемый уровень шума (погрешности) в данных обучения и соответственно степень приближения, с которой функция (103) воспроизведет данные обучения.
- Если
, то это будет соответствовать частному случаю, когда погрешность или любая противоречивость в данных отсутствует и, искомая функция должна точно воспроизвести обучающую выборку. Т.е. задача обучения превращается в задачу многомерной интерполяции.
- Если
, то это будет соответствовать случаю, когда предполагается что в данных обучения одинаково на всей выборке содержится шум, имеющий нормальное распределение со среднеквадратическим отклонением равным
. Задачу обучения можно рассматривать как многомерную аппроксимацию.
- Если же уровень шума и его распределение в пространстве обучения неравномерно но известно, его наличие может быть задано в виде функции
(или достаточно только ее значений в узлах интерполяции).
Рассмотрим теперь коэффициенты в выражении (104).
- Коэффициенты
и
в “идеальном случае” должны быть приблизительно равны и устремлены в бесконечность. В реальных вычислениях в качестве этих коэффициентов можно использовать
при условии нормирования входных значений в диапазоне [-1,1] (они должны быть на несколько порядков больше диапазона изменения входных значений). С увеличением
и
разница от использования функции (104) вместо “идеальной функции” устремляется в область все более низких частот (при разложении искомой функции в спектр) измеряемыми
и все меньше влияет на результаты обучения в области параметрического пространства, где находится обучающая выборка.
- Коэффициент
,назовем его “калибровочным”, связан со свойствами априорной случайной функции. Хотя непосредственно случайные функции в представленных выражениях (103) - (105) не используются, эти выражения выведены на их основе. (Если
и обучение сводится к многомерной интерполяции, значение
можно взять произвольным, поскольку при решении системы (105) и вычислении функции (103) он сократится.)
Процедура вычисления (предлагаемый вариант):

Рис.10. Оценка желаемой дисперсии на единичном расстоянии.
- Калибровка требуется, чтобы найти баланс между возможными погрешностями, неточностями и противоречиями в данных обучения и возможной нелинейностью самой функции, связывающей вход и выход.
- Предположим известно, что искомая функция (103) проходит через некий узел. Для калибровки можно априорно задать желаемый уровень дисперсии множества возможных реализаций
на единичном расстоянии от узла. С увеличением
при вычислениях (103) – (105) все “ большая роль” будет отводиться возможной нелинейности самой функции, с уменьшением – все больше “списываться” на наличие неточностей в данных обучения. При известном
можно вычислить требуемый коэффициент
:
Рис.11. Пример одномерной интерполяции.
- На рис.11. представлен пример одномерной интерполяции (при
). Как видно из рисунка, интерполяция выполнена качественно (отсутствуют осцилляции, которые, например, часто имеют место при использовании интерполяционного многочлена Лагранжа).
- С вводом
, интерполяция легко превращается в аппроксимацию - Рис.12.
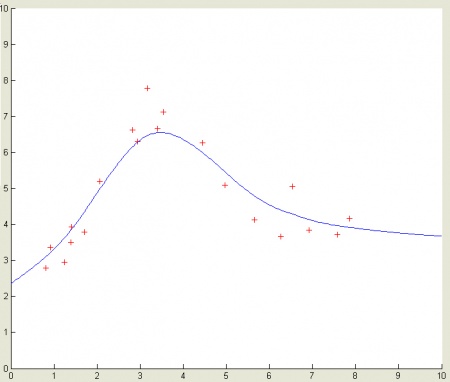
Рис.12. Пример одномерной аппроксимации.
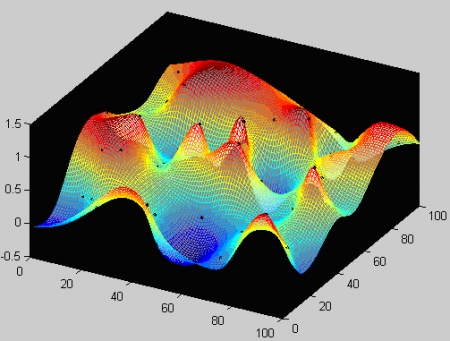
Рис.13. Пример двумерной интерполяции.
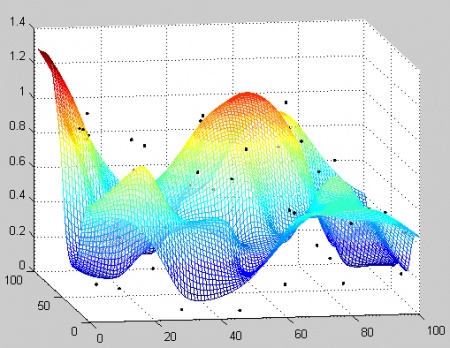
Рис.14. Пример двумерной аппроксимации.
- На Рис. 11 – 14 представлены примеры интерполяции и аппроксимации в одномерном и двумерном случае в целях наглядности результатов. Выражения (103) – (105) могут быть использованы без ограничений для пространства любой размерности.
- Для определения среднеквадратического отклонения возможной ошибки были получены выражения:
- Значение
определяется следующим выражением:
- А коэффициенты
из (108) находятся решением системы уравнений (109):
- Необходимо отметить, что при расчете среднеквадратического отклонения для каждого значения
, необходимо рассчитать индивидуальное значение
и заново решать систему уравнений (109) (хотя вычисления можно упростить, единожды вычислив обратную матрицу).
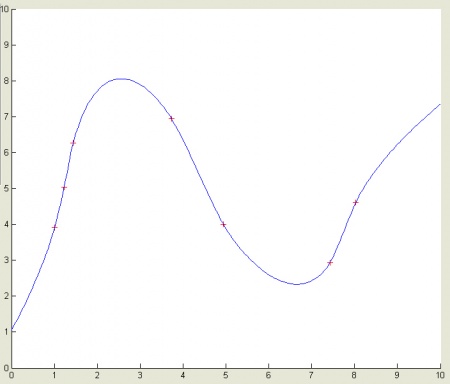
Рис.15. Пример одномерной интерполяции.

Рис.16. Среднеквадратическое отклонение распределения возможной ошибки как случайной величины для найденной функции на Рис.15
- Ожидаемая ошибка функции (103) как случайная величина (исходя из теоретических положений в первой части) будет иметь нормальное распределение с рассчитанным по (107) среднеквадратическим отклонением и математическим ожиданием равным нулю. Зная это, мы можем ее отобразить графически, как показано на Рис.17.

Рис.17. Возможная ожидаемая ошибка, или распределение реализаций случайной функции, удовлетворяющих данным обучения
- С другой стороны, то, что мы можем понимать под возможной ошибкой, представляет собой распределение значений возможных реализаций априорной случайной функции (рассмотренной в теоретической части) которые удовлетворяют данным обучения.
Ниже представлены рисунки, демонстрирующие аппроксимацию.

Рис.18. Пример одномерной аппроксимации.

Рис.19. Распределение реализаций или возможная ожидаемая ошибка (для функции на Рис.18).
- Среднеквадратическая ошибка в (107) отражает разброс значений связанный с возможным распределением реализаций. Если требуется учесть возможный шум в самих данных, то для вычисления среднеквадратического отклонения можно воспользоваться выражением:
Пример. Рассмотрим одномерный случай.
- Предположим, распределение шума (его среднеквадратического отклонения) в области аппроксимации определяется выражением:
- Т.е. в области около нуля шум почти отсутствует и возрастает по мере удаления.

Рис.20. Аппроксимация с учетом распределения шума.

Рис.21. Графическое отображение множества реализаций (с учетом шума).
Демонстрация в среде Matlab.
Предложенный подход к машинному обучению был реализован в виде набора функций в среде Matlab.
Ссылка [52Кб]на файл-архив с функциями.
Кроме самих функций в архиве содержатся программы-демонстрации в виде графического интерфейса пользователя в среде Matlab.
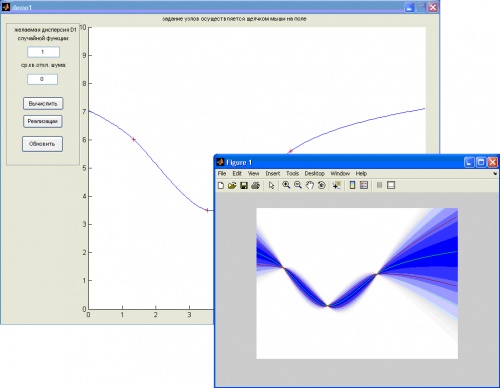
Рис.22. Демонстрация одномерной интерполяции и аппроксимации.
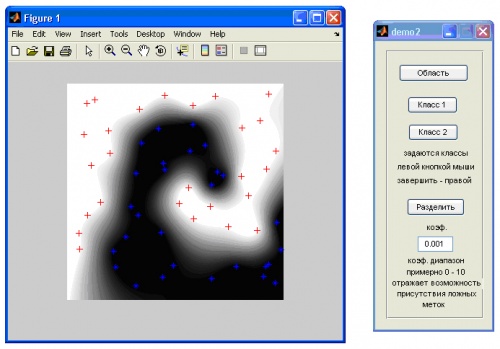
Рис.23. Демонстрация разделения двух классов на плоскости.
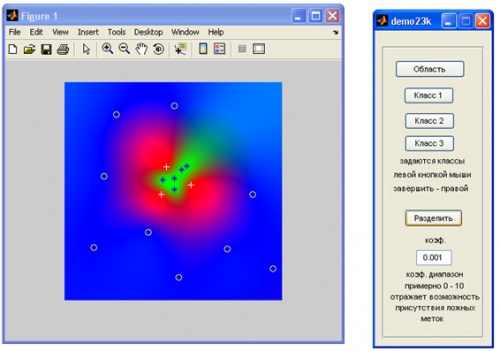
Рис.24. Разделение трех классов на плоскости.
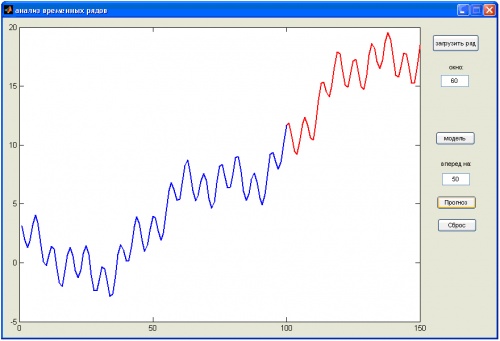
Рис.25. Продолжение временного ряда. Синим цветом – исходный ряд. Красным – прогноз на основе обучения.

