Статистический отчет при создании моделей

Материал из MachineLearning.

Перейти к: навигация, поиск

Содержание

В данной работе приведен обзор статистических методов оценивания качества регрессионных моделей, используемых популярными программами машинного обучения и статистической обработки данных. Приведены примеры вычисления и анализа полученных оценок.

Постановка задачи

Имеется пространство объектов-строк \mathbb{X} = \mathbb{R}^n и пространство ответов \mathbb{Y} = \mathbb{R}. Задана выборка (x_i,\ y_i)_{i=1}^l \in \mathbb{X} \times \mathbb{Y}. Обозначеним:

  • X = \(x_1 <br> \ \vdots\ <br> x_l\)  — матрица информации или матрица плана;
  • w = \(w_1<br> \ \vdots <br> w_n\)  — вектор параметров;
  • y = \(y_1<br>\ \vdots<br>y_l\)  — целевой вектор.

Будем считать, что зависимость имеет вид

y(x) = f(x) + \varepsilon(x),

где f(x)  — некоторая неслучайная функция, \varepsilon(x)  — случайная величина, с нулевым математически ожиданием. В моделях предполагается, что неслучайная составляющая имеет вид:

Требуется численно оценить качество модели при заданном векторе параметров w.

Описание решения

Предполагая, что матрица ковариации вектора ошибки \varepsilon = \(\varepsilon_1 <br> \ \vdots\ <br> \varepsilon_l\) имеет вид \sigma^2 V , где V = diag (v_1, \dots, v_l) (V может быть задана пользователем, иначе выбирается единичная матрица), получаем выражение для оценки параметров w взвешенным методом наименьших квадратов:

\hat w = (X^T V^{-1} X)^{-1} X^T V^{-1} y.

Основными инструментами оценки качества линейной модели является анализ:

Для оценки качества модели линейной регрессии в работе рассматривается

  • анализ регрессионных остатков, включающий в себя:
    • вычисление среднеквадратичной ошибки:

\mathbb{MSE} = \sum_{i=1}^l \left(y_i - f\left(x_i\right)\right)^2;

    • вычисление коэффициента детерминации:

\mathbb{R}^2 = 1 - \frac{\sum_{i=1}^l \left(y_i - f\left(x_i\right)\right)^2}{\sum_{i=1}^l \left(y_i - \bar y\right)^2}, где \bar y = \frac{1}{l} \sum_{i=1}^l y_i;

    • проверку гипотезы о равенстве нулю математического ожидания регрессионных остатков на основе критерия знаков;
    • проверку гипотезы о равенстве дисперсий (пропорциональности с заданными коэффициентами) регрессионных остатков на основе критерия Ансари-Брэдли;
    • проверку гипотезы о нормальности распределения регрессионных остатков на основе критерия хи-квадрат и критерия Жарка-Бера;
  • вычисление расстояния Махаланобиса и Кука;
  • вычисление корреляций признаков, корреляций признаков и значений моделируемой функции и коэффициента множественной регрессии.

Для оценки качества модели логистической регрессии в работе рассматриваются оценки

  • дисперсии шума модели;
  • корреляции и ковариации коэффициентов регрессии;
  • значимости компонент пространства объектов для восстановления ответов;

Вычислительный эксперимент

В данном отчете представлены результаты применения созданного инструмента для анализа модели. Отчет состоит из пяти экспериментов, демонстрирующих работу инструмента на различных по качеству моделях. Модели 1-3 приведены для линейной регрессии, 4-5  — для логистической.

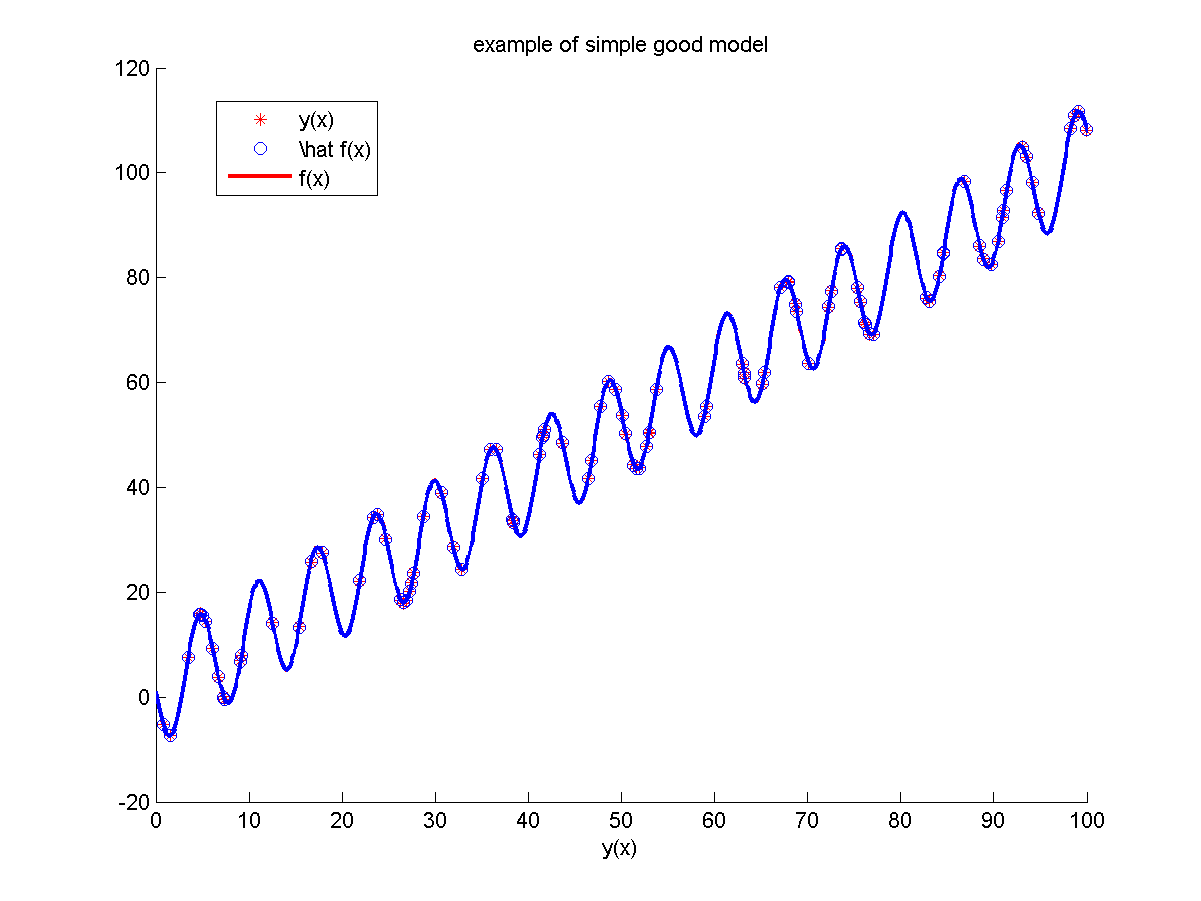
Модель №1

Неизвестная зависимость: y(x) = x - 10 \sin(x) + \exp(x / 100).

Для построения модели использовалось 100 объектов независимо равномерно распределительных на отрезке [0, 100]. В качестве шума использовались независимые случайные величины из распределения N(0, \; 0,1). В качестве признаков использовались x, \; \sin(x), \;\exp(x / 100). Параметры модели подбирались с помощью метода наименьших квадратов.

image:statModelAnalisys01.png

Отчет, построенный программой:

отчет №1.

Модель №2

Неизвестная зависимость: y(x) = x - 10 \sin(x) + \exp(x / 100).

Для построения модели использовалось 100 объектов независимо равномерно распределительных на отрезке [0, 100]. В качестве шума использовались независимые случайные величины из распределения N(0, \; 0,1). В качестве признаков использовались x, \;\exp(x / 100). Параметры модели подбирались с помощью метода наименьших квадратов.

image:statModelAnalisys02.png

Отчет, построенный программой:

отчет №2.

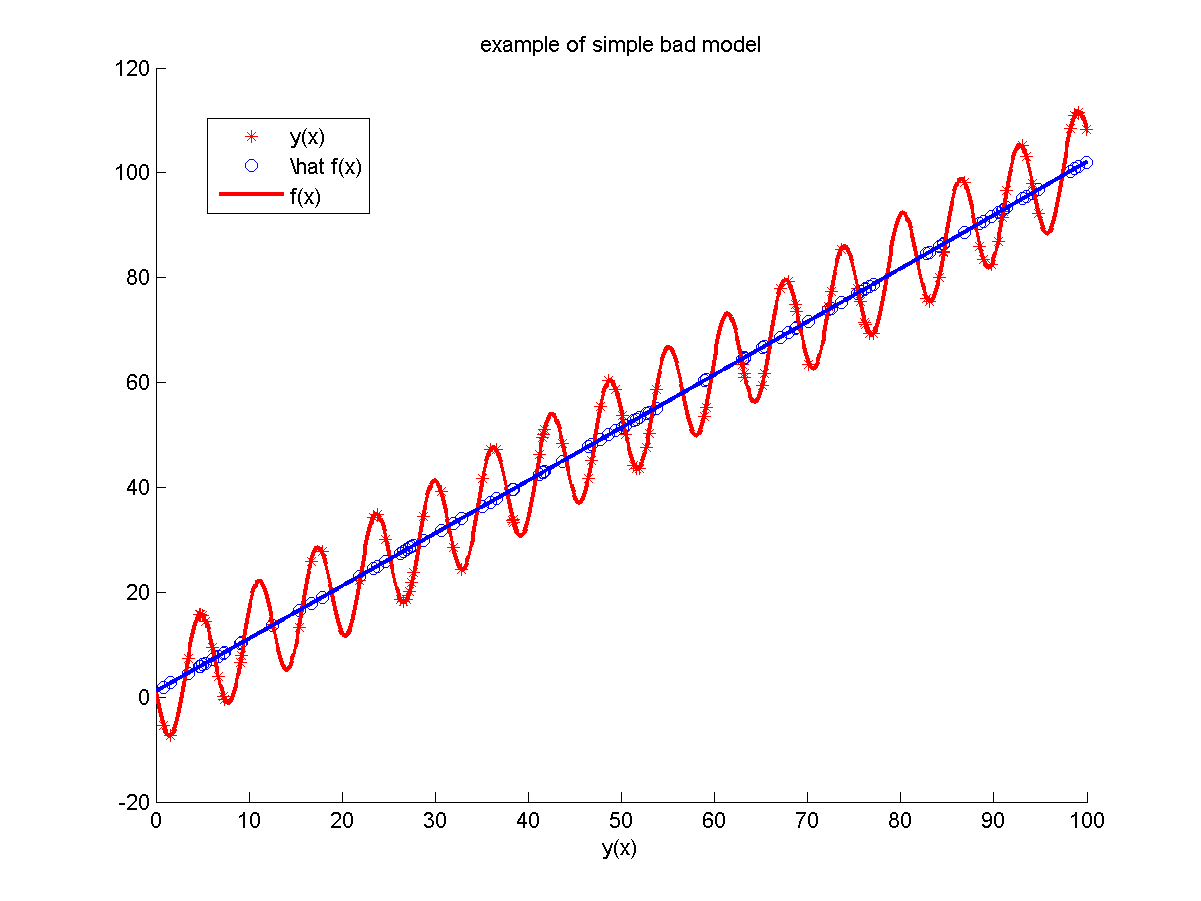
Модель №3

Неизвестная зависимость: y(x) = x - 10 \sin(x) + \exp(x / 100).

Для построения модели использовалось 100 объектов независимо равномерно распределительных на отрезке [0, 100]. В качестве шума использовались независимые случайные величины из распределения N(0, \; x). В качестве признаков использовались y(x) = x - 10 \sin(x) + \exp(x / 100). Параметры модели подбирались с помощью метода наименьших квадратов.

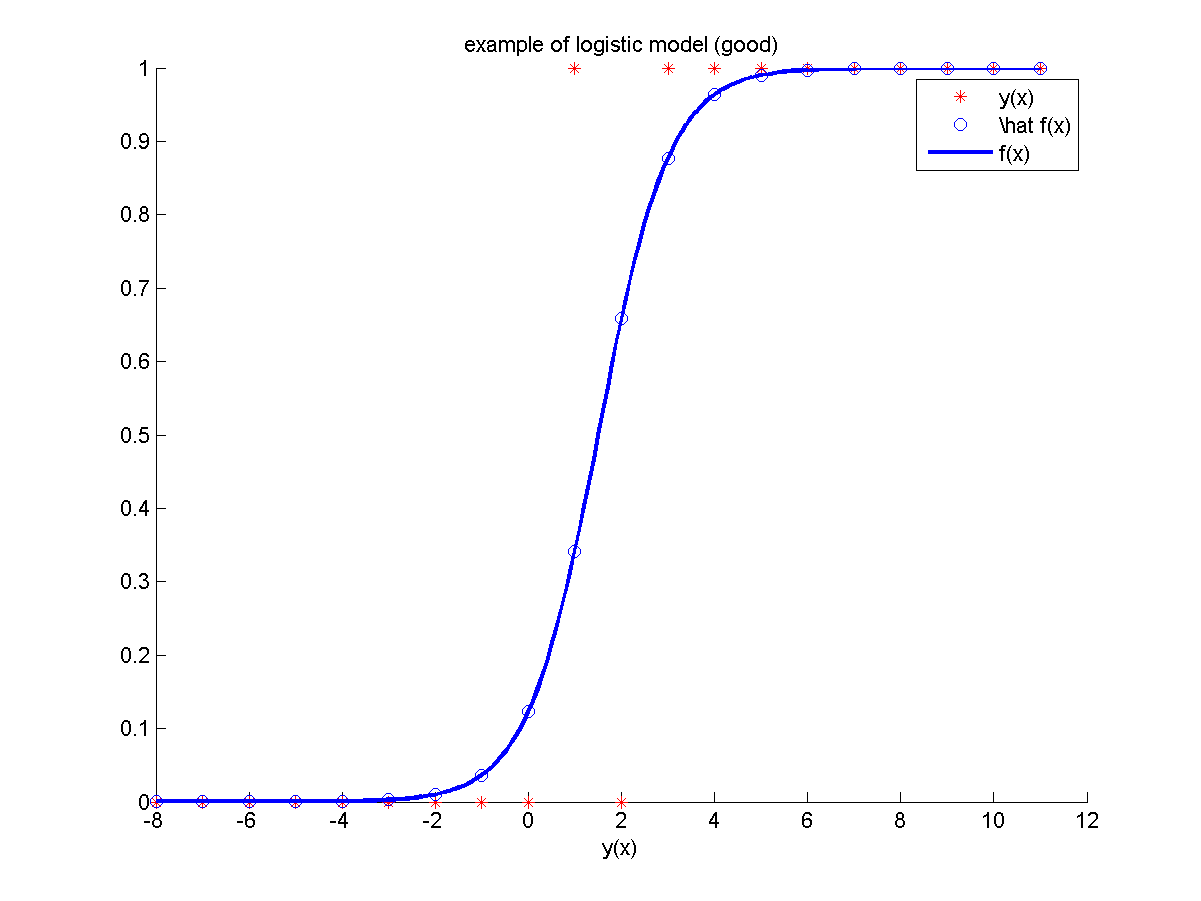
Модель №4

Неизвестная зависимость: y(x) = I(x > 0), . где I(A)  — индикаторная функция множества A .

Для построения модели использовалось 20 объектов из равномерной сетки. Значение в одной из обучающих точек сильно зашумлено. В качестве признаков использовались константа, x .

image:statModelAnalisys04.png

Отчет, построенный программой:

отчет №4.

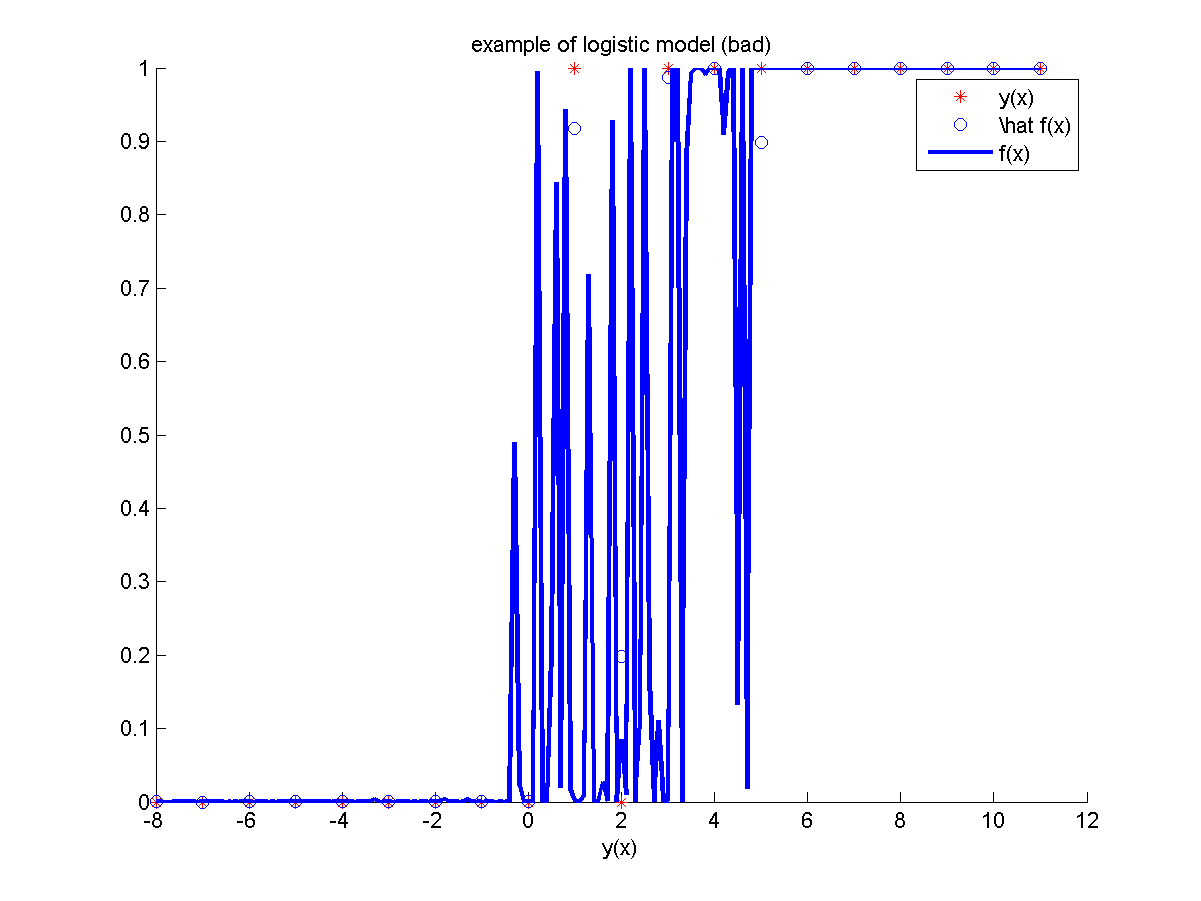
Модель №5

Неизвестная зависимость: y(x) = I(x > 0), . где I(A)  — индикаторная функция множества A .

Для построения модели использовалось 20 объектов из равномерной сетки. Значение в одной из обучающих точек сильно зашумлено. В качестве признаков использовались константа, x и шумовой признак (порожден стандартным нормальным распределением).

image:statModelAnalisys05.png

Отчет, построенный программой:

отчет №5.

Исходный код и полный текст работы

Функция, строящая отчет, и примеры.

Смотри также

Литература

  1. Bishop, C. Pattern Recognition And Machine Learning. Springer. 2006.
  2. Кобзарь А. И. Прикладная математическая статистика. — М.: Физматлит, 2006.
  3. Лагутин М. Б. Наглядная математическая статистика. В двух томах. — М.: П-центр, 2003.
  4. Hosmer W. D. , Lemeshow S. Applied logistic regression - New York: John Wiley & Sons, 2000.


Данная статья была создана в рамках учебного задания.
Студент: Юрий Янович
Преподаватель: В.В. Стрижов
Срок: 28 мая 2009


В настоящее время задание завершено и проверено. Данная страница может свободно правиться другими участниками проекта MachineLearning.ru.

См. также методические указания по использованию Ресурса MachineLearning.ru в учебном процессе.

Источник — «http://machinelearning.ru/wiki/index.php?title=%D0%A1%D1%82%D0%B0%D1%82%D0%B8%D1%81%D1%82%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D0%B9_%D0%BE%D1%82%D1%87%D0%B5%D1%82_%D0%BF%D1%80%D0%B8_%D1%81%D0%BE%D0%B7%D0%B4%D0%B0%D0%BD%D0%B8%D0%B8_%D0%BC%D0%BE%D0%B4%D0%B5%D0%BB%D0%B5%D0%B9»
Личные инструменты