Аппроксимация Лапласа (пример)
Материал из MachineLearning.
(→Постановка задачи) |
(→Пример 1) |
||
| Строка 23: | Строка 23: | ||
Используя '''МНК''' находим оптимальное значение <tex>w_1_{opt}</tex> и <tex>w_2_{opt}</tex> (при которых ''SSE'' минимально). | Используя '''МНК''' находим оптимальное значение <tex>w_1_{opt}</tex> и <tex>w_2_{opt}</tex> (при которых ''SSE'' минимально). | ||
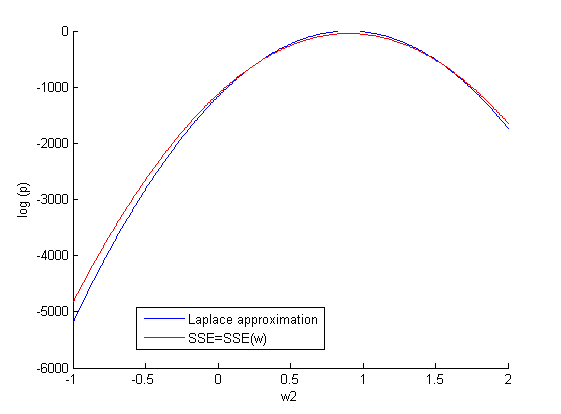
| - | '''При фиксированном''' <tex>w_1=w_1_{opt}</tex> | + | '''При фиксированном''' <tex>w_1=w_1_{opt}</tex> задаем различные значение <tex>w_2</tex> (500 рандомных значений на отрезке [-1;2]) и строим зависимость: |
[[Изображение:Sse(w2)_1.png|center|frame]] | [[Изображение:Sse(w2)_1.png|center|frame]] | ||
| - | <tex>D_{kl}(p_{SSE},p_{lap})=0.0085</tex> | + | <tex>D_{kl}(p_{SSE},p_{lap})=0.0085</tex>. |
| - | '''Повторим эксперимент''', только теперь варируем сразу оба параметра <tex>w_1</tex> и <tex>w_2</tex> | + | '''Повторим эксперимент''', только теперь варируем сразу оба параметра <tex>w_1</tex> и <tex>w_2</tex>: |
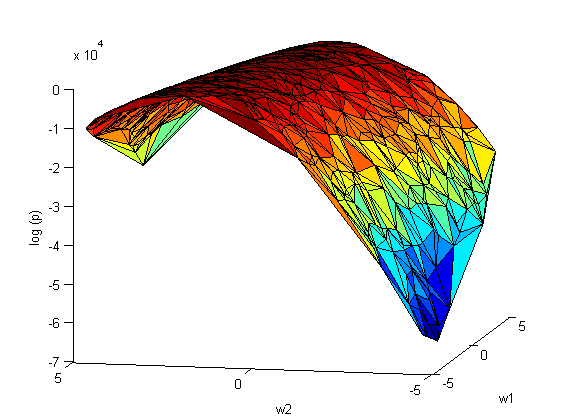
[[Изображение:Sse(w1,w2).png|center|frame|РИС.1.]] | [[Изображение:Sse(w1,w2).png|center|frame|РИС.1.]] | ||
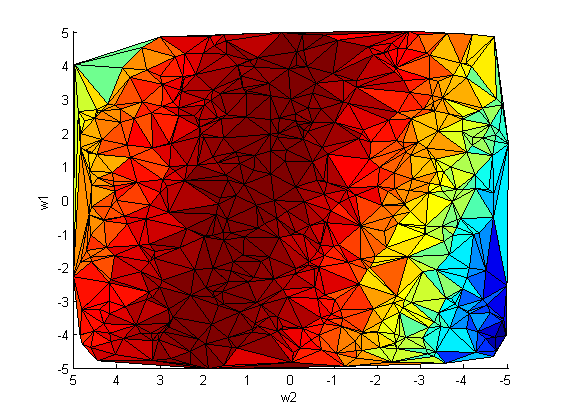
[[Изображение:Sse(w1,w2)_axle_up.png|center|frame|РИС.2. Ось log(p) направлена вверх.]] | [[Изображение:Sse(w1,w2)_axle_up.png|center|frame|РИС.2. Ось log(p) направлена вверх.]] | ||
| - | апроксимация лапласса | + | апроксимация лапласса: |
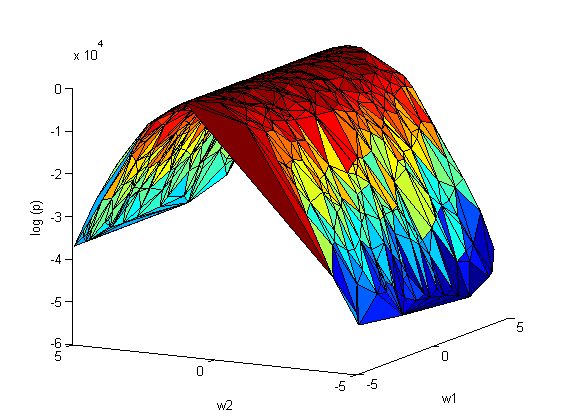
[[Изображение:Sse(w1,w2)_laplas.png|center|frame|Laplace approximation]] | [[Изображение:Sse(w1,w2)_laplas.png|center|frame|Laplace approximation]] | ||
Версия 19:58, 16 ноября 2010
Аппроксимация Лапласа - простой, но широко используемый способ нахождения нормального (Гауссово) распределения для апроксимации заданой плотности вероятности.
Содержание |
Сэмплирование
Сэмплирование – процесс выбора подмножества наблюдаемых величин из данного множества, для дальнейшего его анализа.
Одно из основных приминений методов сэмплирования заключается в оценке мат. ожидания сложных вероятностных распределений: , для которых тяжело делать выборку непосредственно из распределения p(z). Однако, можно подсчитать значение p(z) в любой точке z. Один из наиболее простых методов подсчета мат. ожидаия – разбить ось z на равномерную сетку и подсчитать интеграл как сумму
≅
. Существует несколько методов сэмплирования для создания подходящей выборки длинны L ???.
Постановка задачи
Задана выборка — множество значений свободных переменных и множество
соответствующих им значений зависимой переменной.
Необходимо для выбранной регрессионной модели
показать зависимость среднеквадратичной ошибки от значений параметров модели:
; построить график и сделать апроксимацию Лапласа для него; найти расстояния между получеными зависимостями, используя метрику Кульбака - Лейблера.
Описание алгоритма
метрика Кульбака - Лейблера:
Вычислительный эксперимент
Обозначим плоность распределения SSE как , а его апроксимация лапласса
Пример 1
Задуманная функция . Берем линейную регрессионную модель с 2-мя параметрами:
.
Используя МНК находим оптимальное значение
и
(при которых SSE минимально).
При фиксированном задаем различные значение
(500 рандомных значений на отрезке [-1;2]) и строим зависимость:
.
Повторим эксперимент, только теперь варируем сразу оба параметра и
:
апроксимация лапласса:
На рис.2 наблюдается зависимость между коэффициентами и
. Следовательно, ковариационная матрица cov(w_1,w_2) не будет диагональной.