Байесовские методы машинного обучения (курс лекций, Д.П. Ветров, Д.А. Кропотов)/Задание 1
Материал из MachineLearning.
| Строка 16: | Строка 16: | ||
|- | |- | ||
|} | |} | ||
| + | |||
| + | <br>Рассмотрим несколько упрощенную версию модели 1. Известно, что биномиальное распределение <tex>B(n,p)</tex> при большом количестве испытаний и маленькой вероятности успеха может быть с высокой точностью приближено пуассоновским распределением <tex>Poiss(\lambda)</tex> с <tex>\lambda = np</tex>. Известно также, что сумма двух пуассоновских распределений с параметрами <tex>\lambda_1</tex> и <tex>\lambda_2</tex> есть пуассоновское распределение с параметром <tex>\lambda_1+\lambda_2</tex>. Таким образом, мы можем сформулировать вероятностную модель, которая является приближенной версией модели 1:<br> | ||
| + | '''Модель 2'''<br> | ||
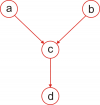
| + | <tex>p(a,b,c,d)=p(d|c)p(c|a,b)p(a)p(b)</tex>,<br> | ||
| + | <tex>d|c \sim c + B(c,p_3)</tex>,<br> | ||
| + | <tex>c|a,b \sim Poiss(ap_1+bp_2)</tex>,<br> | ||
| + | <tex>a \sim R[a_{min},a_{max}]</tex>,<br> | ||
| + | <tex>b \sim R[b_{min},b_{max}]</tex>.<br> | ||
Версия 18:25, 10 октября 2010
| | Внимание! Текст задания находится в стадии формирования. Просьба не рассматривать текущий вариант текста как окончательный вид задания. |
Начало выполнения задания: 11 октября 2010 г.
Срок сдачи: 25 октября 2010 г., 23:59.
Рассмотрим модель посещаемости студентами одного курса лекции по спецкурсу. Пусть аудитория данного спецкурса состоит из студентов профильной кафедры, а также студентов других кафедр. Обозначим через количество студентов, распределившихся на профильную кафедру, а через
— количество студентов других кафедр на курсе. Пусть студенты профильной кафедры посещают спецкурс с некоторой вероятностью
, а студенты остальных кафедр — с вероятностью
. Обозначим через
количество студентов на данной лекции. Тогда случайная величина
есть сумма двух случайных величин, распределенных по биномиальному закону
и
соответственно. Пусть далее на лекции по спецкурсу ведется запись студентов. При этом каждый студент записывается сам, а также, быть может, записывает своего товарища, которого на лекции на самом деле нет (просьба не воспринимать это как руководство к действию в реальности!!). Пусть студент записывает своего товарища с некоторой вероятностью
. Обозначим через
общее количество записавшихся на данной лекции. Тогда случайная величина
представляет собой сумму
и случайной величины, распределенной по биномиальному закону
. Для завершения задания вероятностной модели осталось определить априорные вероятности для
и для
. Пусть обе эти величины распределены равномерно в своих интервалах
и
. Таким образом, мы определили следующую вероятностную модель:
Модель 1
|
Рассмотрим несколько упрощенную версию модели 1. Известно, что биномиальное распределение при большом количестве испытаний и маленькой вероятности успеха может быть с высокой точностью приближено пуассоновским распределением
с
. Известно также, что сумма двух пуассоновских распределений с параметрами
и
есть пуассоновское распределение с параметром
. Таким образом, мы можем сформулировать вероятностную модель, которая является приближенной версией модели 1:
Модель 2
,
,
,
,
.