Интерполяция полиномами Лагранжа и Ньютона
Материал из MachineLearning.
м (→Постановка задачи) |
(викификация, категория) |
||
| (7 промежуточных версий не показаны.) | |||
| Строка 4: | Строка 4: | ||
<tex> y = f(x) </tex>. <br> | <tex> y = f(x) </tex>. <br> | ||
Пусть заданы точки | Пусть заданы точки | ||
| - | <tex> \bf{ | + | <tex> \bf{X} = \{ x_i | i = 1..n \}</tex> |
из некоторой области <tex> \bf D </tex>.<br> | из некоторой области <tex> \bf D </tex>.<br> | ||
Пусть значения функции <tex> f </tex> известны только в этих точках.<br> | Пусть значения функции <tex> f </tex> известны только в этих точках.<br> | ||
| - | Точки <tex> \bf{ | + | Точки <tex> \bf{X} </tex> называют узлами интерполяции.<br> |
| - | <tex> \delta x_i = x_i - x_{i-1}</tex> - | + | <tex> \delta x_i = x_i - x_{i-1}</tex> - шаг интерполяционной сетки.<br> |
Задача интерполяции состоит в поиске такой функции <tex> F </tex> из заданного класса функций, что | Задача интерполяции состоит в поиске такой функции <tex> F </tex> из заданного класса функций, что | ||
<tex> F(x_i) = y_i</tex> | <tex> F(x_i) = y_i</tex> | ||
== Метод решения задачи == | == Метод решения задачи == | ||
| + | ===Полином Лагранжа=== | ||
| + | Представим интерполяционную функцию в виде полинома<br> | ||
| + | <tex>P_n(x) = \sum_{i=0}^n y_i Q_{n,i}(x)</tex><br> | ||
| + | где <tex>Q_{n,i}(x)</tex> - полиномы степели n вида:<br> | ||
| + | <tex>Q_{n,i}(x) = \prod_{j=0, j\neq i}^{n} \frac{(x-x_j)}{(x_i-x_j)}</tex><br> | ||
| + | Очевидно, что <tex>Q_{n,i}(x)</tex> принимает значение 1 в точке <tex>x_i</tex> и 0 в остальных узлах интерполяции. Следовательно в точке <tex>x_i</tex> исходный полином принимает значение <tex>y_i</tex><br> | ||
| + | Таким образом, построенный полином <tex>P_n(x)</tex> является интерполяционным полиномом для функции | ||
| + | <tex> y = f(x) </tex> на сетке <tex> \bf{X} </tex>. <br> | ||
| + | ===Полином Ньютона=== | ||
| + | Интерполяционный полином в форме Лагранжа не удобен для вычислений тем, что при увеличении числа узлов интерполяции приходится перестраивать весь полином заново.<br> | ||
| + | Перепишем полином Лагранжа в другом виде:<br> | ||
| + | <tex>P_n(x) = P_0(x) + \sum_{i=1}^n{(P_i(x) - P_{i-1}(x))} </tex><br> | ||
| + | где <tex>P_i(x)</tex> - полиномы Лагранжа степени i ≤ n.<br> | ||
| + | Пусть <tex>Q_i(x) = P_i(x) - P_{i-1}(x) \qquad(*)</tex> <br>. Этот полином имеет степень i и обращается в нуль при | ||
| + | <tex>x = x_0, x = x_1, ..., x = x_{i-1}{</tex>. <br> | ||
| + | Поэтому он представим в виде:<br> | ||
| + | <tex>Q_i(x) = A_i(x - x_0)...(x - x_{i-1})</tex>, | ||
| + | где <tex>A_i</tex> - коэффициент при <tex>x^i</tex>. Так как <tex>x^i</tex> не входит в <tex>P_{i-1}(x)</tex>, то <tex>A_i</tex> совпадает с коэффициентом при <tex>x^i</tex> в полиноме <tex>P_i(x)</tex>. Таким образом из определения <tex>P_i(x)</tex> получаем:<br> | ||
| + | <tex> A_i = \sum_{k=0}^i\frac{f(x_k)}{w_{k,i}}</tex><br> | ||
| + | где <br> | ||
| + | <tex> w_{k,i} = (x_k - x_0)...(x_k - x_{k-1})(x_k - x_{k+1})...(x_k - x_i)</tex><br> | ||
| + | Препишем формулу <tex>\qquad(*)</tex> в виде <br> | ||
| + | <tex>P_n(x) = P_{n-1} + A_n(x - x_0)...(x - x_{n-1})</tex><br> | ||
| + | Рекуррентно выражая <tex>P_i(x)</tex> пролучам окончательную формулу для полинома: <br> | ||
| + | <tex>P_n(x) = A_0 + A_1(x-x_0) + ...+ A_n(x - x_0)...(x - x_{n-1})</tex><br> | ||
| + | Такое представление полинома удобно для вычисления, потому что увеличение числа узлов на единицу требует добавления только одного слагаемого.<br> | ||
| + | ==Погрешность интерполирования== | ||
| + | Поставим вопрос о том, насколько хорошо интерполяционный полином <tex>P_n(x)</tex> приближает функцию <tex>f(x)</tex> на отрезке [a,b].<br> | ||
| + | Рассмотри м остаточный член:<br> | ||
| + | <tex>R_n(x) = f(x) - P_n(x)</tex>, x ∈ [a, b].<br> | ||
| + | По определению интерполяционного полинома <tex><br>R_n(x_i) = 0, x_i \in \bf X</tex> <br> | ||
| + | поэтому речь идет об оценке <tex>R_n(x)</tex> при значениях <tex>x \not= x_i</tex>.<br> | ||
| + | Пусть <tex>f(x)</tex> имеет непрерывную (n+1) производную на отрезке [a, b].<br> | ||
| + | Тогда погрешность определяется формулой:<br> | ||
| + | <tex>|R_n(x)| = \frac{f^{n+1}(\varepsilon)}{(n+1)!}w_{n+1}(x)</tex>,<br> | ||
| + | где <tex>w_{n+1} = (x - x_0)...(x - x_n)</tex>,<br> | ||
| + | <tex>\varepsilon </tex>- точка из [a, b].<br> | ||
| + | Так как точка <tex>\varepsilon </tex> наизвестна, то эта формула позволяет только оценить погрешность:<br> | ||
| + | <tex>|R_n(x)| \le \frac{M_{n+1}}{(n+1)!}|w_{n+1}(x)|</tex><br> | ||
| + | где <tex>M_{n+1} = \max_{x\in[\alpha, \beta]}|f^{n+1}(x)|</tex><br> | ||
| + | Из вида множетеля <tex>w_{n+1}</tex> следует, что оценка имеет смысл только при <tex>x \in [x_0, x_n]</tex>. Если это не так, то при интерполяции используются полиномы низких степеней (n = 1,2). <br> | ||
| + | == Выбор узлов интерполяции == | ||
| + | Так как от выбора узлов завист точность интерполяции, то возникает вопрос о том, как их выбирать. | ||
| + | С помощью выбора узлов можно минимизировать значение <tex>w_{n+1}</tex> в оценке погрешности. Эта задача решается с помощью многочлена Чебышева [1]: <br> | ||
| + | <tex>T_{n+1}(x) = \frac{(b - a)}{(2^{2n+1})}cos ((n + 1)arccos \frac{2x - (b + a)}{(b - a)})</tex><br> | ||
| + | В качестве узлов следут взять корни этого многочлена, то есть точки: <br> | ||
| + | <tex>x_k = \frac{a + b}{2} + \frac{b - a}{2} \cos\frac{(2k + 1)\pi}{2(n + 1)}</tex> | ||
== Пример == | == Пример == | ||
| + | В качастве примера рассмотрим интерполяцию синуса. | ||
| + | Возьмем равномерную решетку x = [-3,-1.5,0,1.5,3];<br> | ||
| + | Интерполяция полиномом Лагранжа:<br> | ||
| + | [[Изображение:1sinalg.gif]]<br> | ||
| + | Ошибка(максимальное отклонение от sin(x) на отрезке):0.1423<br> | ||
| + | Интерполяция полиномом Ньютона:<br> | ||
| + | Ошибка:<br> | ||
| + | Возьмем решетку x с узлами в корнях полинома Чебышева= [-2.8531,-1.7632,0,1.7634,2.8532];<br> | ||
| + | Интерполяция полиномом Лагранжа:<br> | ||
| + | [[Изображение:2sinlag.gif]]<br> | ||
| + | Ошибка: 0.0944<br> | ||
| + | Интерполяция полиномом Ньютона:<br> | ||
| + | Ошибка:<br> | ||
| + | == Рекомендации программисту == | ||
| + | |||
| + | == Выводы == | ||
== Литература == | == Литература == | ||
| + | # Самарский А.А. Гулин А.В. Численные методы 1989г. | ||
| + | # Костомаров Д.П., Фаворский А.П. Вводные лекции по численным методам | ||
| + | |||
| + | == Смотри также == | ||
| + | * [[Практикум ММП ВМК, 4й курс, осень 2008]] | ||
| + | |||
| + | {{stub}} | ||
| + | |||
| + | [[Категория:Учебные задачи]] | ||
Текущая версия
Содержание |
Постановка задачи
Пусть задана функция
.
Пусть заданы точки
из некоторой области
.
Пусть значения функции известны только в этих точках.
Точки называют узлами интерполяции.
- шаг интерполяционной сетки.
Задача интерполяции состоит в поиске такой функции из заданного класса функций, что
Метод решения задачи
Полином Лагранжа
Представим интерполяционную функцию в виде полинома
где - полиномы степели n вида:
Очевидно, что принимает значение 1 в точке
и 0 в остальных узлах интерполяции. Следовательно в точке
исходный полином принимает значение
Таким образом, построенный полином является интерполяционным полиномом для функции
на сетке
.
Полином Ньютона
Интерполяционный полином в форме Лагранжа не удобен для вычислений тем, что при увеличении числа узлов интерполяции приходится перестраивать весь полином заново.
Перепишем полином Лагранжа в другом виде:
где - полиномы Лагранжа степени i ≤ n.
Пусть
. Этот полином имеет степень i и обращается в нуль при
.
Поэтому он представим в виде:
,
где
- коэффициент при
. Так как
не входит в
, то
совпадает с коэффициентом при
в полиноме
. Таким образом из определения
получаем:
где
Препишем формулу в виде
Рекуррентно выражая пролучам окончательную формулу для полинома:
Такое представление полинома удобно для вычисления, потому что увеличение числа узлов на единицу требует добавления только одного слагаемого.
Погрешность интерполирования
Поставим вопрос о том, насколько хорошо интерполяционный полином приближает функцию
на отрезке [a,b].
Рассмотри м остаточный член:
, x ∈ [a, b].
По определению интерполяционного полинома
поэтому речь идет об оценке при значениях
.
Пусть имеет непрерывную (n+1) производную на отрезке [a, b].
Тогда погрешность определяется формулой:
,
где ,
- точка из [a, b].
Так как точка наизвестна, то эта формула позволяет только оценить погрешность:
где
Из вида множетеля следует, что оценка имеет смысл только при
. Если это не так, то при интерполяции используются полиномы низких степеней (n = 1,2).
Выбор узлов интерполяции
Так как от выбора узлов завист точность интерполяции, то возникает вопрос о том, как их выбирать.
С помощью выбора узлов можно минимизировать значение в оценке погрешности. Эта задача решается с помощью многочлена Чебышева [1]:
В качестве узлов следут взять корни этого многочлена, то есть точки:
Пример
В качастве примера рассмотрим интерполяцию синуса.
Возьмем равномерную решетку x = [-3,-1.5,0,1.5,3];
Интерполяция полиномом Лагранжа:
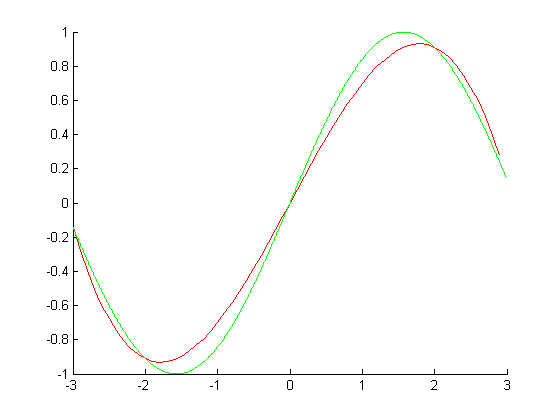
Ошибка(максимальное отклонение от sin(x) на отрезке):0.1423
Интерполяция полиномом Ньютона:
Ошибка:
Возьмем решетку x с узлами в корнях полинома Чебышева= [-2.8531,-1.7632,0,1.7634,2.8532];
Интерполяция полиномом Лагранжа:
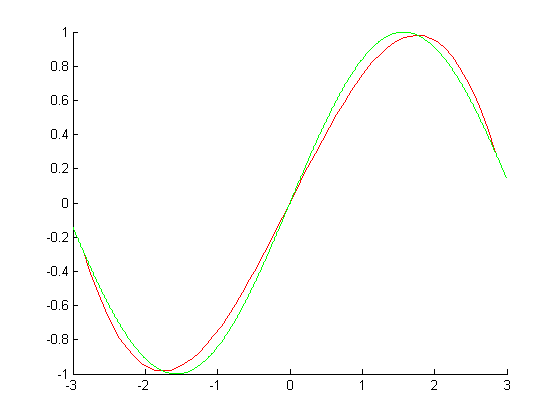
Ошибка: 0.0944
Интерполяция полиномом Ньютона:
Ошибка:
Рекомендации программисту
Выводы
Литература
- Самарский А.А. Гулин А.В. Численные методы 1989г.
- Костомаров Д.П., Фаворский А.П. Вводные лекции по численным методам

