Переобучение
Материал из MachineLearning.
|
Обобщающая способность (generalization ability, generalization performance). Говорят, что алгоритм обучения обладает способностью к обобщению, если вероятность ошибки на тестовой выборке достаточно мала или хотя бы предсказуема, то есть не сильно отличается от ошибки на обучающей выборке. Обобщающая способность тесно связана с понятиями переобучения и недообучения.
Переобучение, переподгонка (overtraining, overfitting) — нежелательное явление, возникающее при решении задач обучения по прецедентам, когда вероятность ошибки обученного алгоритма на объектах тестовой выборки оказывается существенно выше, чем средняя ошибка на обучающей выборке. Переобучение возникает при использовании избыточно сложных моделей.
Недообучение — нежелательное явление, возникающее при решении задач обучения по прецедентам, когда алгоритм обучения не обеспечивает достаточно малой величины средней ошибки на обучающей выборке. Недообучение возникает при использовании недостаточно сложных моделей.
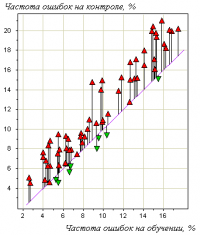
Пример. На рисунке справа показан эффект переобучения в одной задаче медицинского прогнозирования. Точки на графике соотвествуют различным методам обучения. Каждая точка получена путём усреднения по большому числу разбиений исходной выборки из 72 прецедентов на обучающую подвыборку и контрольную. Горизонтальная ось — частота ошибок на обучении; вертикальная — на контроле. Хорошо видно, что точки имеют систематическое смещение вверх относительно диагонали графика.
О природе переобучения
Эмпирическим риском называется средняя ошибка алгоритма на обучающей выборке. Метод минимизации эмпирического риска (empirical risk minimization, ERM) наиболее часто применяется для построения алгоритмов обучения. Он состоит в том, чтобы в рамках заданной модели выбрать алгоритм, имеющий минимальное значение средней ошибки на заданной обучающей выборке.
С переобучением метода ERM связано два утверждения, которые на первый взгляд могут показаться парадоксальными.
Утверждение 1. Минимизация эмпирического риска не гарантирует, что вероятность ошибки на тестовых данных будет мала. Легко строится контрпример — абсурдный алгоритм обучения, который минимизирует эмпирический риск до нуля, но при этом абсолютно не способен обучаться. Алгоритм состоит в следующем. Получив обучающую выборку, он запоминает её и строит функцию, которая сравнивает предъявляемый объект с запомненными обучающими объектами. Если предъявляемый объект в точности совпадает с одним из обучающих, то эта функция выдаёт для него запомненный правильный ответ. Иначе выдаётся произвольный ответ (например, случайный или всегда один и тот же). Эмпирический риск алгоритма равен нулю, однако он не восстанавливает зависимость и не обладает никакой способностью к обобщению.
Вывод: для успешного обучения необходимо не только запоминать, но и обобщать.
Утверждение 2. Переобучение появляется именно вследствие минимизации эмпирического риска. Пусть задано конечное множество из D алгоритмов, которые допускают ошибки независимо и с одинаковой вероятностью. Число ошибок любого из этих алгоритмов на заданной обучающей выборке подчиняется одному и тому же биномиальному распределению. Минимум эмпирического риска — это случайная величина, равная минимуму из D независимых одинаково распределённых биномиальных случайных величин. Её ожидаемое значение уменьшается с ростом D. Соотвественно, с ростом D увеличивается переобученность — разность вероятности ошибки и частоты ошибок на обучении.
В данном модельном примере легко построить доверительный интервал переобученности, так как функция распределения минимума известна. Однако в реальной ситуации алгоритмы имеют различные вероятности ошибок, не являются независимыми, а множество алгоритмов, из которого выбирается лучший, может быть бесконечным. По этим причинам вывод количественных оценок переобученности является сложной задачей, которой занимается теория вычислительного обучения. До сих пор остаётся открытой проблема сильной завышенности верхних оценок вероятности переобучения.
Утверждение 3. Переобучение связано с избыточной сложностью используемой модели. Всегда существует оптимальное значение сложности модели, при котором переобучение минимально.
Пример.
Рассмотрим задачу аппроксимации вещественной функции по обучающей выборке из 50 точек
. Это равномерная сетка на отрезке
.
В качестве модели рассмотрим полиномы заданной степени :
В качестве метода обучения возьмём метод наименьших квадратов:
Таким образом, функция потерь квадратична:
.
Возьмём контрольную выборку — также равномерную сетку на отрезке , узлы которой находятся в точности между узлами первой сетки:
.
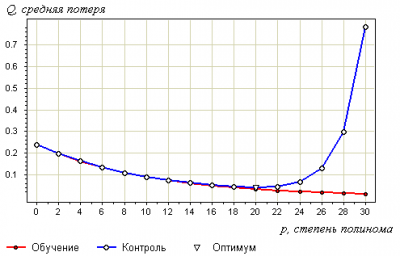
Зададимся вопросом:
что будет на контрольной выборке при увеличении степени полинома ?
Степень связана с числом свободных параметров модели, то есть играет роль сложности модели.
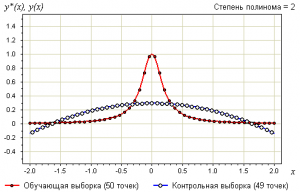
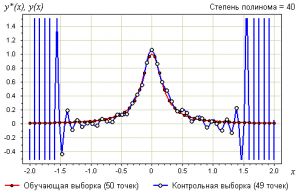
Ниже показаны графики самой выборки и аппроксимирующей функции:
- при
— недообучение.
- при
— оптимальная сложность модели.
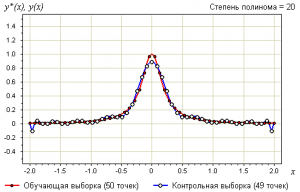
- при
— неустойчивость и переобучение.
Определения
Основные обозначения:
— подмножество (выборка) объектов из множества объктов
,
— множество алгоритмов,
— функция потерь, значение
есть величина потерь, возникающих при применении алгоритма
к объекту
.
Средней потерей алгоритма на выборке
называется величина
Пусть — вероятностное пространство.
Ожидаемой потерей алгоритма
называется величина
Если функция бинарная (возвращяет либо 0, либо 1), то
называется частотой ошибок, а
— вероятностью ошибки алгоритма
.
Не столь важно, что скрывается за термином «алгоритм». Это могут быть в частности, решающие правила в задачах классификации и распознавания образов, функции регрессии в задачах восстановления регрессии илипрогнозирования, и т. п.
Определение.
Методом обучения (или алгоритмом обучения) называется отображение , которое произвольной обучающей выборке
ставит в соответствие некоторый алгоритм
.
Вероятность переобучения (частотное определение)
Определение.
Переобученностью алгоритма относительно контрольной выборки
называется разность
Определение.
Вероятностью переобучения называется вероятность того, что величина переобученности превысит заданный порог :
где вероятность можно понимать в смысле равномерного распределения на множестве всех
разбиений выборки
на наблюдаемую обучающую
и скрытую контрольную
.
Вероятность переобучения может быть измерена эмпирически методом Монте-Карло, см. также скользящий контроль:
где —
случайных разбиений заданной выборки
на обучающую подвыборку
и контрольную подвыборку
.
Вероятность переобучения (вероятностное определение)
Определение.
Переобученностью алгоритма называется разность
Определение.
Вероятностью переобучения называется вероятность того, что величина переобученности превысит заданный порог :
где — вероятность в пространстве случайных незавичимых выборок
, взятых из одного и того же неизвестного распределения.
Недостатки вероятностного определения:
- Сложность эмпирического измерения
при неизвестной вероятностной мере.
- Большинство верхних оценок для
выводятся через оценки для
с помощью Леммы о симетризации. При это снижается точность оценок.
Теоретические верхние оценки переобученности
Сложность
Оценки Вапника-Червоненкиса, размерность Вапника-Червоненкиса
Оценки, основанные на самоограничении (self-bounding)
Оценки, основанные на последовательности выборов (microchoice bounds)
Оценки, основанные на расслоении семейства алгоритмов (shell bounds)
Разделимость
Оценки, основанные на отступах (margin-based bounds)
Устойчивость
Устойчивость алгоритма обучения (algorithmic stability)
Эмпирическое измерение переобучения
См. также
- Расслоение и сходство алгоритмов (виртуальный семинар)
- Слабая вероятностная аксиоматика
- Полигон алгоритмов
- Радемахеровская сложность
Ссылки
Overfitting — статья о переобучении в англоязычной Википедии.
Литература
- Hastie, T., Tibshirani, R., Friedman, J. The Elements of Statistical Learning, 2nd edition. — Springer, 2009. — 533 p. (подробнее)
- Vapnik V.N. Statistical learning theory. — N.Y.: John Wiley & Sons, Inc., 1998. [1]
- Воронцов, К. В. Комбинаторная теория надёжности обучения по прецедентам: Дис. док. физ.-мат. наук: 05-13-17. — Вычислительный центр РАН, 2010. — 271 с. (подробнее)