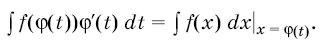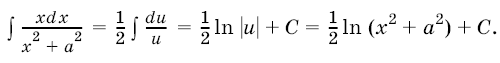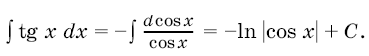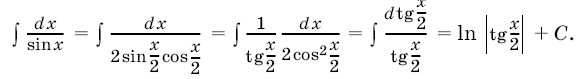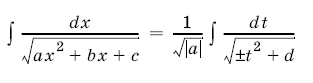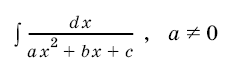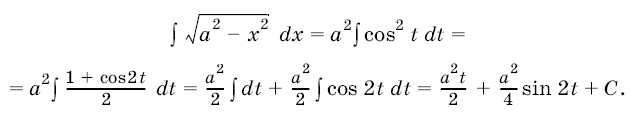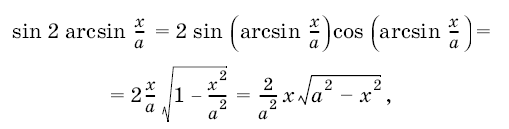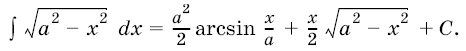Стандартизация задач с помощью замены переменных
Материал из MachineLearning.
Содержание |
Введение
Формула замены переменных в определенном интеграле
Формула замены переменных в неопределенном интеграле
Рассмотрим свойство неопределенного интеграла, часто оказывающееся полезным при вычислении первообразных элементарных функций.
Теорема.
Пусть функции и
определены соответственно на промежутках
и
, причем
. Если функция
имеет на
первообразную
и, следовательно,
(1)
а функция дифференцируема на
, то функция
имеет на
, первообразную
и
(2)
Формула (1) называется формулой интегрирования подстановкой, а именно подстановкой . Это название объясняется тем, что если формулу (2) записать в виде
то будет видно, что, для того чтобы вычислить интеграл 
), можно сделать подстановку , вычислить интеграл
и затем вернуться к переменной
, положив
.
Примеры.
1. Для вычисления интеграла естественно сделать подстановку
, тогда
2. Для вычисления интеграла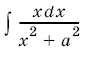 
удобно применить подстановку
:
3. При вычислении интегралов вида 
полезна подстановка
:
Например,
Иногда, прежде чем применить метод интегрирования подстановкой, приходится проделать более сложные преобразования подынтегральной функции:
Отметим, что формулу (2) бывает целесообразно использовать и в обратном порядке, т.е. справа палево. Именно, иногда удобно вычисление интеграла с помощью соответствующей замены переменного
свести к вычислению интеграла
(если этот интеграл в каком-то смысле «проще» исходного).
В случае, когда функция имеет обратную
, перейдя в обеих частях формулы (2) к переменной
с помощью подстановки
и поменяв местами стороны равенства, получим
Эта формула называется обычно формулой интегрирования заменой переменной.
Для того чтобы существовала функция , обратная
, в дополнение к условиям теоремы достаточно, например, потребовать, чтобы на рассматриваемом промежутке
функция
была строго монотонной. В этом случае, существует однозначная обратная функция
.
4. Интегралы вида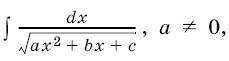 
в том случае, когда подкоренное выражение неотрицательно на некотором промежутке, легко сводятся с помощью заме¬ны переменного к табличным.
Действительно, замечая, что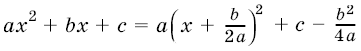 
, сделаем замену переменной 
и положим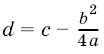 
. Тогда 
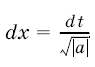и, в силу формулы (2), получим
(перед стоит знак плюс, если а > 0, и знак минус, если а < 0). Интеграл, стоящий в правой части равенства, является табличным. Найдя его по соответствующим формулам и вернувшись от переменной
к переменной
, получим искомый интеграл.
Подобным же приемом вычисляются и интегралы вида
5. Интеграл 
можно вычислить с помощью подстановки
. Имеем
, поэтому
Подставляя это выражение и замечая, что
окончательно будем иметь
Заметим, что для проверки результата, полученного при вычислении неопределенного интеграла, достаточно его продифференцировать, после чего должно получиться подынтегральное выражение вычисляемого иптеграла.
Квадратурные формулы интерполяционного типа
Формула замены переменных в кратном интеграле
Сведения об интегралах с бесконечными пределами
Соотношение равномощности
Заключение
Литература
- Л.Д. Кудрявцев. Курс математического анализа в 3 томах.
- З.И. Гурова, С.Н. Каролинская, А.П. Осипова. Математический анализ. Начальный курс с примерами и задачами.
- А.А. Самарский, А.В. Гулин. Численные методы М.: Наука, 1989.
- http://de.ifmo.ru/bk_netra/page.php?index=42&layer=1&tutindex=21#2
- http://sesia5.ru/vmat/gl5/21.html
