Статистический анализ данных (курс лекций, К.В.Воронцов)/2011, ФУПМ

Материал из MachineLearning.

(Различия между версиями)

Версия 14:15, 10 апреля 2011

Содержание

1 Задание 1. Исследование свойств одномерных статистических критериев на модельных данных
- 1.1 Пример задания
- 1.2 Задания
2 Задание 2. Анализ реальных данных
3 Литература
4 Ссылки

Задание 1. Исследование свойств одномерных статистических критериев на модельных данных

Необходимо провести исследование одного из классических критериев проверки статистических гипотез. Интерес представляет поведение достигаемого уровня значимости (p-value) как функции размера выборок и параметров распределения. В соответствии с индивидуальными параметрами задания необходимо указанным способом сгенерировать одну или несколько выборок из заданного распределения, выполнить проверку гипотезы при помощи соответствующего критерия, а затем многократно повторить эту процедуру для различных значений параметров. По результатам расчётов необходимо построить следующие графики:

график зависимости достигаемого уровня значимости от значений параметров при однократном проведении эксперимента;
график зависимости достигаемого уровня значимости от значений параметров, усреднённого по большому количеству повторений эксперимента (например, по 100, 500, 1000 повторений — чем больше, тем лучше);
график с эмпирическими оценками мощности критерия для разных значений параметров.

В качестве оценки мощности принимается доля отвержений нулевой гипотезы среди всех проверок. То есть, если эксперимент повторялся $k$ раз для каждого набора значений параметра, и в $m$ из $k$ случаев гипотеза была отвергнута на некотором фиксированном уровне значимости $\alpha$ (примем $\alpha=0.05$ ), оценкой мощности будет отношение $m/k$ .

Необходимо сдать: отчёт с описанием алгоритма, построенными графиками и выводами (объяснение полученных результатов моделирования, границы применимости критерия и т.д.), а также файл с текстом программы на использованном языке (Matlab, R, и т.д.), при выполнении которой проводятся указанные в задаче вычисления и на экран выводятся графики, соответствующие имеющимся в отчёте.

Задание принимается до девятого апреля.

Пример задания

Исследуем поведение классического двухвыборочного критерия Стьюдента для проверки гипотезы однородности против альтернативы сдвига при разных значениях параметров.

$x^n = (x_1,\ldots,x_n)\sim N(\mu_1,\sigma),\;\; y^n = (y_1,\ldots,y_n)\sim N(\mu_2,\sigma);$

$H_0\,:\; \mu_1=\mu_2,$

$H_1\,:\; \mu_1\neq\mu_2.$

$\sigma = 1; \;\;\; \mu_1=0; \;\;\; \mu_2=0\,:\,0.05\,:\,3; \;\;\; n=5\,:\,1\,:\,50.$

При каждом значении $\mu_2$ выборки для разных значений $n$ генерируются независимо.

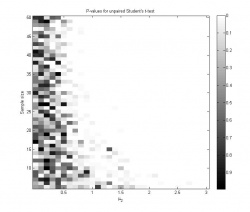
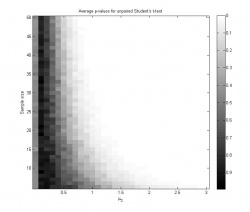
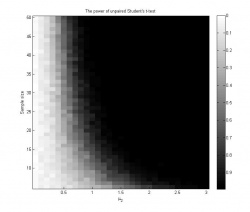
Графики 1 и 2 иллюстрируют зависимость достигаемого уровня значимости от размера выборки и среднего $\mu_2$ . На графике 3 показана зависимость мощности критерия от параметров задачи; мощность в каждой точке оценивается как доля экспериментов, в которых гипотеза была отвергнута на уровне значимости $\alpha=0.05$ .

График 1: значения достигаемого уровня значимости при однократной генерации выборок.

График 2: значения достигаемого уровня значимости, усрёднённые по 100 экспериментам.

График 3: значения эмпирических оценок мощности критерия при проведении 100 экспериментов ( $\alpha=0.05$ ).

Видно, что при $\mu_2=0$ среднее значение достигаемого уровня значимости при многократном повторении эксперимента равно 0.5 для любого размера выборки. Это логично, так как при $\mu_2=0$ нулевая гипотеза справедлива, и достигаемый уровень значимости имеет равномерное распределение на $[0,1].$
При $n>20$ и $\mu_2>1$ критерий имеет достаточную мощность, и нулевая гипотеза чаще всего отвергается.
При размере выборки до 50 элементов и среднем второй выборки $\mu_2<0.5$ критерий практически не способен отклонить гипотезу однородности, мощность в этой области изменения параметров низка.
При большой разнице между средними выборок $(\mu_2>2)$ критерий достаточно уверенно отвергает гипотезу однородности даже на выборках небольшого размера (5-6 элементов).

Задания

Устойчивость критериев к нарушению предположений

Исследовать поведение параметрических критериев, предполагающих нормальность данных, при зашумлении выборок наблюдениями, взятыми из равномерного распределения. Построить графики вида 1, 2, 3, сделать выводы о чувствительности критерия к зашумлению.

Двухвыборочный критерий Стьюдента для независимых выборок.

$x^n \sim p_1\cdot N(\mu_1,1)+ \left(1-p_1\right)\cdot U\left[-a+\mu_1,a+\mu_1\right]$ — выборка длины $n$ из смеси нормального $N(\mu_1,1)$ и равномерного $U\left[-a+\mu_1,a+\mu_1\right]$ распределений с весами $p_1$ и $1-p_1$ соответственно (при генерации выборки используется случайный датчик — если его значение не превосходит $p_1$ , то добавляем в выборку элемент, взятый из нормального распределения, иначе — элемент, взятый из равномерного).
$y^n \sim p_2\cdot N(\mu_2,1)+ \left(1-p_2\right)\cdot U\left[-a+\mu_2,a+\mu_2\right]$ — аналогичная выборка.
$H_0\,:\; \mu_1=\mu_2, \;\; H_1\,:\; \mu_1\neq\mu_2;$
$\mu_1=0; \;\; \mu_2=-2\,:\,0.01\,:\,2.$

Кононенко Даниил: $p_1=0.8, \;\; p_2=1, \;\; a=1, \;\; n=15\,:\,5\,:\,200.$

Голкин Александр: $p_1=0.9, \;\; p_2=1, \;\; a=5, \;\; n=15\,:\,5\,:\,200.$

Завадский Глеб: $p_1=p_2=0.8, \;\; a=1, \;\; n=15\,:\,5\,:\,200.$

Чугунов Кирилл: $p_1=p_2=0.9, \;\; a=5, \;\; n=15\,:\,5\,:\,200.$

Корниенко Алексей: $p_1=p_2=0\,:\,0.01\,:\,1, \;\; a=1, \;\; n=150.$

Кузнецов Михаил: $p_1=p_2=0\,:\,0.01\,:\,1, \;\; a=5, \;\; n=100.$

Критерий Фишера для проверки равенства дисперсий.

$x^n \sim p_1\cdot N(0,\sigma_1)+ \left(1-p_1\right)\cdot U\left[-a,a\right]$ — выборка длины $n$ из смеси нормального $N(0,\sigma_1)$ и равномерного $U[-a,a]$ распределений с весами $p_1$ и $1-p_1$ соответственно (при генерации выборки используется случайный датчик — если его значение не превосходит $p_1$ , то добавляем в выборку элемент, взятый из нормального распределения, иначе — элемент, взятый из равномерного).
$y^n \sim p_2\cdot N(0,\sigma_2)+ \left(1-p_2\right)\cdot U\left[-a,a\right]$ — аналогичная выборка.
$H_0\,:\; \sigma_1=\sigma_2, \;\; H_1\,:\; \sigma_1\neq\sigma_2.$
$\sigma_1=1, \;\; \sigma_2=0.1\,:\,0.05\,:\,4.$

Иванов Николай: $p_1=0.8, \;\; p_2=1, \;\; a=1, \;\; n=15\,:\,5\,:\,200.$

Рубцов Александр: $p_1=0.9, \;\; p_2=1, \;\; a=5, \;\; n=15\,:\,5\,:\,200.$

Рукина Дарья: $p_1=p_2=0.8, \;\; a=1, \;\; n=15\,:\,5\,:\,200.$

Савгиров Арш: $p_1=p_2=0.9, \;\; a=5, \;\; n=15\,:\,5\,:\,200.$

Спиридонов Роман: $p_1=p_2=0\,:\,0.01\,:\,1, \;\; a=1, \;\; n=150.$

Стукалюк Владимир: $p_1=p_2=0\,:\,0.01\,:\,1, \;\; a=5, \;\; n=100.$

Влияние связок на поведение статистических критериев

Многие статистические критерии неявно предполагают, что выборка извлечена из абсолютно непрерывного распределения, что значит, что вероятность наличия в ней одинаковых элементов равна нулю. Необходимо исследовать поведение такого критерия в случае наличия в выборке совпадающих значений. Построить графики вида 1, 2, 3, сделать выводы о чувствительности критерия к наличию связок.

Для генерации выборки со связками может использоваться округление элементов выборки, либо следующая процедура:

генерируется выборка $x^n$ размера $n$ из указанного в задаче распределения;
в вариационном ряду выборки $x^n_{\left(i\right)}$ выбираются $k$ непересекающихся пар элементов $\left(x_{\left(i\right)}, x_{\left(i+1\right)}\right)$ , лежащих ближе всего друг к другу;
для всех $k$ выбранных пар элементы выборки $x_{\left(i\right)}$ и $x_{\left(i+1\right)$ заменяются их средним.

Статистические критерии, проверяющие гипотезу нормальности.

$x^n\sim p\cdot N\left(0,1\right)+\left(1-p\right)\cdot U\left[a,b\right]$ — выборка длины $n$ из смеси нормального $N\left(0,1\right)$ и равномерного $U\left[a,b\right]$ распределений с весами $p$ и $1-p$ соответственно (при генерации выборки используется случайный датчик — если его значение не превосходит $p$ , то добавляем в выборку элемент, взятый из нормального распределения, иначе — элемент, взятый из равномерного);
$H_0\,:\; x^n$ распределена нормально; $H_1\,:\; x^n$ распределена по какому-то другому закону.
$n=20\,:\,5\,:\,200.$

Сунгуров Дмитрий: критерий Андерсона-Дарлинга, указанная процедура порождения связок, $k=\frac{n}{3}, \;\;p=0\,:\,0.01\,:\,1, \;\; -a=b=3.$

Животовский Никита: критерий Шапиро-Уилка, указанная процедура порождения связок, $k=\frac{n}{2}, \;\;p=0\,:\,0.01\,:\,1, \;\; -a=b=3.$

Мафусалов Александр: критерий Андерсона-Дарлинга, округление элементов выборки до десятых, $p=0\,:\,0.01\,:\,1, \;\; a=-1, \;\; b=1.5.$

Сечин Павел: критерий Шапиро-Уилка, округление элементов выборки до десятых, $p=0\,:\,0.01\,:\,1, \;\; a=-2, \;\; b=3.$

Критерий Уилкоксона-Манна-Уитни.

$x^n \sim N(0,1),\;\;y^n \sim N(\mu,1);$
$H_0\,:\; \mu=0, \;\;\; H_1\,:\; \mu\neq 0;$
$\mu=0\,:\,0.01\,:\,2.$

Джамтырова Раиса: элементы обеих выборок округляются до десятых, $n=10\,:\,5\,:\,200.$

Ивкин Никита: элементы обеих выборок округляются до 0.5, $n=10\,:\,5\,:\,200.$

Пронин Яков: указанная процедура порождения связок (в обеих выборках), $n=10\,:\,5\,:\,200, \;\; k=\frac{n}{3}.$

Фирстенко Александр: указанная процедура порождения связок (в обеих выборках), $n=50, \;\; k=0\,:\,1\,:\,30.$

Анализ чувствительности критериев к редактированию выборки

Известно, что исключение из выборки определённых наблюдений зачастую может достаточно сильно повлиять на результат анализа. Необходимо исследовать чувствительность указанного критерия к редактированию выборки, построить графики вида 1, 2, 3, сделать выводы.

Одновыборочный критерий Стьюдента.

$x^n \sim N(\mu,\sigma);$
$H_0\,:\; \mu=0, \;\;\; H_1\,:\; \mu>0.$
При каждом значении параметра $\mu$ генерируется выборка размера $n$ , проводится проверка гипотезы $H_0$ , затем по некоторому правилу из выборки исключается один из элементов, проверка гипотезы повторяется, затем исключается ещё один, и т.д. Обозначим за $k$ максимальное число исключённых в таком процессе элементов.

Фадеев Илья: $n=100,\;\;k=50,\;\;\sigma=1,\;\;\mu=-1\,:\,0.01\,:\,1,\;\;$ на каждом шаге исключается максимальный элемент.

Берновский Михаил: $n=200,\;\;k=100,\;\;\sigma=5,\;\;\mu=-2\,:\,0.02\,:\,2,\;\;$ на каждом шаге исключается максимальный элемент.

Бессарабов Никита: $n=100,\;\;k=50,\;\;\sigma=2,\;\;\mu=-2\,:\,0.02\,:\,2,\;\;$ на каждом шаге исключается минимальный элемент.

Гнедков Игорь: $n=200,\;\;k=100,\;\;\sigma=5,\;\;\mu=-3\,:\,0.03\,:\,3,\;\;$ на каждом шаге исключается минимальный элемент.

Двухвыборочный критерий Стьюдента.

$x^n \sim N\left(\mu_1,1\right), \;\; y^m \sim N\left(\mu_2,\sigma\right);$
$H_0\,:\; \mu_1=\mu_2, \;\;\; H_1\,:\; \mu_1\neq\mu_2.$
$\mu_1=0, \;\; \mu_2=-2\,:\,0.01\,:\,2.$
На каждом шаге генерируются выборки исходной длины, проводится проверка гипотезы $H_0$ , затем по некоторому правилу из указанной выборки исключается один из элементов, проверка гипотезы повторяется, затем исключается ещё один, и т.д. Обозначим за $k$ максимальное число исключённых в таком процессе элементов.

Савинов Николай: $n=m=100, \;\; \sigma = 1, \;\; k=30, \;\;$ на каждом шаге исключается максимальный элемент $y^m$ .

Татарников Дмитрий: $n=m=50, \;\; \sigma = 2, \;\; k=20, \;\;$ на каждом шаге исключается минимальный элемент $y^m$ .

Зайцев Евгений: $n=50, \;\; m=150\;\; \sigma = 3, \;\; k=50, \;\;$ на каждом шаге исключается максимальный элемент $y^m$ .

Морозов Алексей: $n=100, \;\; m=50; \;\; \sigma = 2, \;\; k=30, \;\;$ на каждом шаге исключается минимальный элемент $x^n$ .

Быстрый Роман: $n=150, \;\; m=100; \;\; \sigma = 3, \;\; k=50, \;\;$ на каждом шаге исключается максимальный элемент $x^n$ .

Задание 2. Анализ реальных данных

Ниже приведены описания анализируемых данных и постановки задач. Сами данные каждый студент может получить по электронной почте после сдачи первого задания. При проведении анализа можно пользоваться любыми доступными программными средствами. Необходимо предоставить подробный письменный отчёт по проведённому исследованию, содержащий выводы и описания каждого этапа анализа — используемые методы, обоснование их применимости, промежуточные результаты вычислений, графики. Помимо выводов, касающихся математических особенностей решения, необходимо включить в отчёт заключения, сформулированные в терминах предметной области, которые могли бы быть понятны гипотетическому заказчику-нематематику.

Задание должно быть засчитано на момент сдачи экзамена.

Внешний вид и привлекательность самок мечехвостов

Изучалось влияние внешних характеристик самок морских ракообразных мечехвостов на их привлекательность для самцов. Выборка состоит из данных о наблюдениях над 173 особями и содержит закодированные данные о размере самок, их весе, цвете, состоянии панциря, а также о количестве спутников.

Кузнецов Михаил: построить функцию, по внешним параметрам самки предсказывающую, будет ли у неё хотя бы один спутник. Оценить значимость каждого фактора.

Кононенко Даниил: построить функцию, по внешним параметрам самки предсказывающую количество спутников у самки. Оценить значимость каждого фактора.

Состав сигарет

По 25 видам сигарет приведены следующие данные: название бренда, содержание смолы и никотина (мг), вес (г), количество моноксида углерода (CO), выделяемого при сгорании (мг).

Бессарабов Никита: Построить функцию, предсказывающую количество выделяемого при сгорании моноксида углерода. Оценить значимость каждого фактора.

Размеры черепа древних египтян

Было измерено 150 черепов, найденных при раскопках в Египте. Находки относятся к пяти различным временным периодам. Для каждого черепа известны: максимальная ширина, базибрегматическая высота, базиальвеолярная длина, высота носа, примерная дата формирования. Была выдвинута гипотеза о том, что изменение этих параметров со временем может свидетельствовать о скрещивании египтян с другими популяциями.

Мафусалов Александр: проверить, есть ли различия между размерами черепов различных временных периодов, если есть, то какие периоды отличаются друг от друга.

Зайцев Евгений: построить функцию, позволяющую отнести череп к одному из приведённых временных периодов по известным линейным размерам. Оценить значимость каждого фактора.

Фирстенко Александр: построить функцию, позволяющую по линейным размерам черепа определить доверительный интервал для даты его формирования.

Летальность пациентов с сепсисом

По 454 пациентам с сепсисом (лихорадка, тахикардия, тахипноэ и острая недостаточность по крайней мере одной системы органов) имеются следующие данные: оценка начального состояния по шкале APACHE острых и хронических функциональных изменений, факт наступления смерти в течение 30 дней после начала исследования (для каждого значения APACHE score приведены общее число пациентов в таком состоянии и соответствующее число пациентов, умерших в течение 30 дней).

Татарников Дмитрий: оценить вероятность наступления в 30-дневный срок летального исхода в зависимости от исходного состояния. Построить функции, дающие точечную оценку и границы 95% доверительного интервала.

Линейные размеры тысячефранковых банкнот

Банкнота в 1000 швейцарских франков серии, действовавшей в период с 1911 по 1958. Красным обозначены измеренные величины.

Имеются данные измерений двухсот швейцарских тысячефранковых банкнот, бывших в обращении в первой половине XX века. Сто из банкнот были настоящими, а сто - поддельными. Измерены следующие величины: $X_1$ — длина банкноты, $X_2$ —ширина банкноты с левой стороны, $X_3$ —ширина банкноты с правой стороны, $X_4$ —расстояние от нижнего края до рамки рисунка, $X_5$ — расстояние от нижнего края до рамки рисунка, $X_6$ — длина диагонали рисунка.

Фадеев Илья: построить функцию, оценивающую по данным измерений вероятность того, что имеющаяся банкнота фальшивая, и 95% доверительный интервал для этой вероятности.

Животовский Никита: построить функции, оценивающие вероятность того, что имеющаяся банкнота фальшивая, по признакам $X_1-X_3$ и по признакам $X_4-X_6$ . Сравнить эффективность выявления фальшивых купюр по двум группам признаков, сделать выводы.

Вкус и химический состав сыра чеддер

30 разновидностей сыра чеддер было проанализировано как с точки зрения химического состава, так и с помощью дегустаторов. Для каждой разновидности известны: оценка вкуса, полученная путём усреднения оценок, выставленных несколькими дегустаторами, логарифмы концентраций уксусной кислоты и сульфида водорода, концентрация молочной кислоты.

Ивкин Никита: построить функцию, по химическому составу сыра предсказывающую его оценку дегустаторами, и границы доверительного интервала для неё.

Савинов Николай: построить функцию, позволяющую по оценке вкуса и логарифмам концентраций уксусной кислоты и сульфида водорода восстанавливать концентрацию молочной кислоты. Оценить значимость каждого фактора.

Литература

Кобзарь А. И. Прикладная математическая статистика. — М.: Физматлит, 2006.

Ссылки

Источник — «http://machinelearning.ru/wiki/index.php?title=%D0%A1%D1%82%D0%B0%D1%82%D0%B8%D1%81%D1%82%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D0%B9_%D0%B0%D0%BD%D0%B0%D0%BB%D0%B8%D0%B7_%D0%B4%D0%B0%D0%BD%D0%BD%D1%8B%D1%85_%28%D0%BA%D1%83%D1%80%D1%81_%D0%BB%D0%B5%D0%BA%D1%86%D0%B8%D0%B9%2C_%D0%9A.%D0%92.%D0%92%D0%BE%D1%80%D0%BE%D0%BD%D1%86%D0%BE%D0%B2%29/2011%2C_%D0%A4%D0%A3%D0%9F%D0%9C»

Категория: Учебные курсы

@@ Строка 144: / Строка 144: @@
 ::Фадеев Илья: построить функцию, оценивающую по данным измерений вероятность того, что имеющаяся банкнота фальшивая, и 95% доверительный интервал для этой вероятности.
 ::Животовский Никита: построить функции, оценивающие вероятность того, что имеющаяся банкнота фальшивая, по признакам <tex>X_1-X_3</tex> и по признакам <tex>X_4-X_6</tex>. Сравнить эффективность выявления фальшивых купюр по двум группам признаков, сделать выводы.
+=== Вкус и химический состав сыра чеддер ===
+разновидностей сыра чеддер было проанализировано как с точки зрения химического состава, так и с помощью дегустаторов. Для каждой разновидности известны: оценка вкуса, полученная путём усреднения оценок, выставленных несколькими дегустаторами, логарифмы концентраций уксусной кислоты и сульфида водорода, концентрация молочной кислоты.
+::Ивкин Никита: построить функцию, по химическому составу сыра предсказывающую его оценку дегустаторами, и границы доверительного интервала для неё.
+::Савинов Николай: построить функцию, позволяющую по оценке вкуса и логарифмам концентраций уксусной кислоты и сульфида водорода восстанавливать концентрацию молочной кислоты. Оценить значимость каждого фактора.
 = Литература =