Статистический анализ данных (курс лекций, К.В.Воронцов)/2013, ФУПМ

Материал из MachineLearning.

Версия от 13:04, 20 апреля 2013; Riabenko (Обсуждение | вклад)

(разн.) ← Предыдущая | Текущая версия (разн.) | Следующая → (разн.)

Содержание

1 Оценки
2 Задание 1. Исследование свойств одномерных статистических критериев на модельных данных
- 2.1 Пример задания
- 2.2 Задания
  - 2.2.1 Анализ поведения схожих критериев
3 Задание 2. Анализ реальных данных
- 3.1 Задания
4 Литература
5 Ссылки

Оценки

Студент	#1 (2 балла)	Участие в семинаре
Адуенко Александр	2	2
Бочкарева Валерия	1.9
Варфоломеева Анна	1.9
Глебов Антон	2
Ефимов Кирилл	2
Иванова Алина	1.8
Клочков Егор
Кузьмин Арсентий	2
Лобастов Степан	2
Медведникова Мария	2
Стенин Сергей	2
Смоляков Дмитрий
Целых Влада	2
Цыганова Светлана	2
Шпакова Татьяна	2
Шульга Александр

Штраф за просрочку сдачи заданий начисляется из расчета 0.1 балла за сутки.
Задание считается сданным на момент получения проверяющим письма с отчётом (и кодом, если это указано в задании), при условии отсутствия необходимости внесения дополнений и исправлений.

Задание 1. Исследование свойств одномерных статистических критериев на модельных данных

Необходимо провести исследование одного или нескольких классических критериев проверки статистических гипотез. Интерес представляет поведение достигаемого уровня значимости (p-value) как функции размера выборок и параметров распределения. В соответствии с индивидуальными параметрами задания необходимо указанным способом сгенерировать одну или несколько выборок из заданного распределения, выполнить проверку гипотезы при помощи соответствующего критерия, а затем многократно повторить эту процедуру для различных значений параметров. По результатам расчётов необходимо построить требуемые в задании графики, среди которых могут быть следующие:

график зависимости достигаемого уровня значимости от значений параметров при однократном проведении эксперимента;
график зависимости достигаемого уровня значимости одного или двух критериев от значений параметров, усреднённого по большому количеству повторений эксперимента (например, по 1000 повторений);
график с эмпирическими оценками мощности одного или двух критериев для разных значений параметров.

В качестве оценки мощности принимается доля отвержений нулевой гипотезы среди всех проверок. То есть, если эксперимент повторялся $k$ раз для каждого набора значений параметров, и в $m$ из $k$ случаев гипотеза была отвергнута на некотором фиксированном уровне значимости $\alpha$ (примем $\alpha=0.05$ ), оценкой мощности будет отношение $m/k.$

Необходимо сдать: выполненный в Tex или Microsoft Word отчёт с описанием алгоритма, построенными графиками и выводами (объяснение полученных результатов моделирования, границы применимости критерия и т.д.), а также код на R, Матлабе или Питоне, при запуске которого на экран выводятся графики, соответствующие имеющимся в отчёте.

Задание принимается до 23:59 31.03.

Пример задания

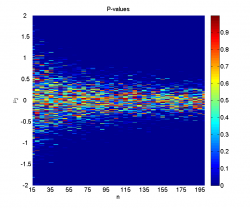
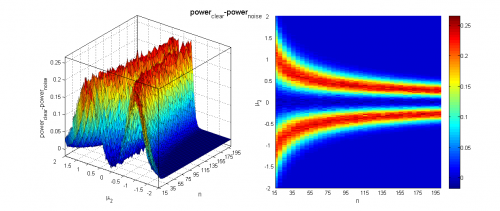
Исследуем чувствительность классического двухвыборочного критерия Стьюдента для проверки гипотезы однородности против альтернативы сдвига при зашумлении выборок наблюдениями, взятыми из равномерного распределения.

$X_1^n, \;\; X_{1i} \sim 0.9\cdot N(\mu_1,1)+ 0.1\cdot U\left[-5+\mu_1,5+\mu_1\right]$ — выборка длины $n$ из смеси стандартного нормального $N(\mu_1,1)$ и равномерного $U\left[-5+\mu_1,5+\mu_1\right]$ распределений с весами $0.9$ и $0.1$ соответственно (при генерации выборки используется случайный датчик — если его значение не превосходит $0.9$ , то добавляем в выборку элемент, взятый из нормального распределения, иначе — элемент, взятый из равномерного).

$X_2^n, \;\; X_{2i} \sim 0.9\cdot N(\mu_2,1)+ 0.1\cdot U\left[-5+\mu_2,5+\mu_2\right]$ — аналогичная выборка.

$H_0\,:\; \mu_1=\mu_2, \;\; H_1\,:\; \mu_1\neq\mu_2.$

$\mu_1=0, \;\; \mu_2=-2\,:\,0.01\,:\,2, \;\; n=15\,:\,5\,:\,200.$

При каждом значении $\mu_2$ выборки для разных значений $n$ генерируются независимо.

Значения достигаемого уровня значимости при однократной генерации выборок.

Значения достигаемого уровня значимости, усрёднённые по 3000 экспериментам.

Значения эмпирических оценок мощности критерия при проведении 3000 экспериментов $(\alpha=0.05).$

Заметим, что однократная генерация выборок даёт достаточно нестабильные результаты, не позволяя точно оценить границы области, где нулевая гипотеза отклоняется, поэтому и необходимо усреднение по большому числу экспериментов.

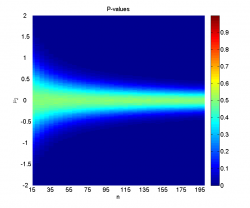
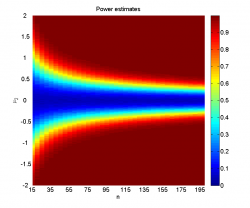
Видно, что при достаточно большой разнице между средними и большом размере выборок наличие шума не мешает уверенно отклонять гипотезу однородности. Когда, наоборот, разница между средними невелика (меньше 0.2-0.5 в зависимости от размера выборок), мощность близка к нулю, а среднее значение достигаемого уровня значимости колеблется около 0.5, что логично, так как его распределение при справедливости нулевой гипотезы равномерно на $[0,1]$ .

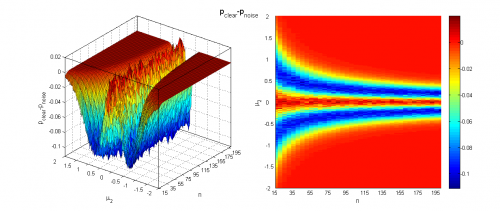
Чтобы оценить вклад зашумления выборок, оценим при всех значениях параметра мощность критерия и средний достигаемый уровень значимости на аналогичных выборках без шума и сравним результаты.

Разность средних достигаемых уровней значимости на выборках без шума и с шумом.

Разность эмпирических оценок мощности на выборках без шума и с шумом.

Видно, что наличие шума всё меньше влияет на работу критерия с ростом объёма выборок и разницы между их средними. Тем не менее, в некоторых областях изменения параметров потеря мощности из-за 10% зашумления может составлять до 20%, а средний достигаемый уровень значимости может быть выше на 0.1.

Отметим, что приведённые количественные выводы справедливы только для шума рассматриваемой структуры.

Задания

Анализ поведения схожих критериев

Требуется исследовать поведение указанной пары статистических критериев, подходящих для решения одной и той же задачи, сравнить мощность и достигаемые уровни значимости и сделать выводы о границах применимости критериев. Необходимо для каждого из критериев построить графики зависимости достигаемых уровней значимости и оценок мощностей от параметров, и показать, в каких областях изменения параметров предпочтительнее использовать тот или иной критерий. Для получения более гладких графиков рекомендуется применять оба критерия к одним и тем же выборкам, а не генерировать их отдельно для каждого критерия.

$X_1^n, \;\; X_{1i} \sim Ber(p_1),\;\;X_2^n, \;\; X_{2i} \sim Ber(p_2), \;\; corr(X_{1i}, X_{2i})=\rho;$
$H_0\,:$ выборки независимы, $\;H_1\,:\,H_0$ неверна.
Чтобы сгенерировать коррелированные Бернуллиевские случайные величины, используется следующий метод^[1]. Пусть $t\left(\lambda\right)$ — случайная величина, имеющая распределение Пуассона с параметром $\lambda$ . Обозначим $\lambda_1 = -\log p_1, \;\; \lambda_2 = -\log p_2, \;\; \lambda_{12} = \log\left(1+\rho\sqrt{\frac{1-p_1}{p_1} \frac{1-p_2}{p_2} }\right).$
Искомую пару случайных величин $X_{1i},X_{2i}$ можно получить следующим образом:
$X_{1i} = \left[t_1\left(\lambda_1-\lambda_{12}\right) + t_3\left(\lambda_{12}\right)\right], <br> X_{2i} = \left[t_2\left(\lambda_2-\lambda_{12}\right) + t_3\left(\lambda_{12}\right)\right],$
где квадратные скобки обозначают индикаторную функцию.
Метод работает при $\rho\geq0;$ для случаев $\rho<0$ генерируются выборки с корреляцией $\left|\rho\right|,$ после чего одна из выборок инвертируется (нули и заменяются на единицы и наоборот).

Адуенко: $p_1=\frac{1}{2}, \;\; p_2 = 0.01\,:\,0.01\,:\,0.99, \;\; \rho = -1\,:\,0.01\,:\,1, \;\; n = 30.$ Сравнить критерий хи-квадрат и точный критерий Фишера.

Бочкарева: $p_1=\frac{1}{2}, \;\; p_2 = \frac{1}{2}, \;\; \rho = -1\,:\,0.01\,:\,1, \;\; n = 10\,:\,1\,:\,50.$ Сравнить G-критерий и точный критерий Фишера.

Варфоломеева: $p_1=0.01\,:\,0.01\,:\,0.99, \;\; p_2 = 0.01\,:\,0.01\,:\,0.99, \;\; \rho = 0.75, \;\; n = 30.$ Сравнить G-критерий и критерий хи-квадрат.

$X^n, \;\; X_i\sim Ber(p);$
$H_0\,:\, p=\frac{1}{2}, \;\; H_1\,:\, p\neq\frac{1}{2};$
$p=0.01\,:\,0.01\,:\,0.99, \;\; n=5\,:\,1\,:\,50.$

Ефимов: сравнить критерии, основанные на доверительных интервалах Вальда и Уилсона (нулевая гипотеза отвергается на уровне значимости 5%, если 95% доверительный интервал для параметра не содержит $\frac{1}{2}$ ).

$X^n, \;\; X_i\sim N(\mu,\sigma);$
$H_0\,:$ среднее значение $X$ равно нулю, $H_1\,:$ среднее значение $X$ не равно нулю;
$\mu=-2\,:\,0.01\,:\,2, \;\; \sigma=1, \;\; n=5\,:\,1\,:\,50.$

Глебов: сравнить одновыборочные T- и Z-критерии.

Иванова: сравнить одновыборочный T-критерий и критерий знаковых рангов Уилкоксона.

Клочков: сравнить одновыборочный перестановочный критерий и критерий знаковых рангов Уилкоксона.

Шульга: сравнить Z-критерий и одновыборочный перестановочный критерий для известной дисперсии.

$X_1^n, \;\; X_{1i} \sim N(\mu_1, \sigma_1^2),\;\;X_2^m, \;\; X_{2i} \sim N(\mu_2, \sigma_2^2);$
$H_0\,:$ дисперсии выборок равны, $H_1\,:$ дисперсии выборок не равны;
$\mu_1=0, \;\; \sigma_1=1.$

Кузьмин: $\mu_2=0, \;\; \sigma_2 = 0.5\,:\,0.01\,:\,2, \;\; n=m=5\,:\,1\,:\,50.$ Сравнить критерий Фишера и WM-критерий.

Лобастов: $\mu_2=-5\,:\,0.05\,:\,5, \;\; \sigma_2 = 0.5\,:\,0.01\,:\,2, \;\; n=m=50.$ Сравнить WM-критерий и критерий Зигеля-Тьюки.

Медведникова: $\mu_2=1, \;\; \sigma_2 = 0.5\,:\,0.01\,:\,2, \;\; n=30, \;\; m=5\,:\,1\,:\,50.$ Сравнить критерий Фишера и критерий Зигеля-Тьюки.

Стенин: $\mu_2=0, \;\; \sigma_2 = 0.5\,:\,0.01\,:\,2, \;\; n=m=5\,:\,1\,:\,50.$ Сравнить WM-критерий и перестановочный критерий.

$X^n, \;\; X \sim p\cdot N(0,1)+ \left(1-p\right)\cdot U\left[-a,a\right]$ — выборка длины $n$ из смеси стандартного нормального $N(0,1)$ и равномерного $U\left[-a,a\right]$ распределений с весами $p$ и $1-p$ соответственно (при генерации выборки используется случайный датчик — если его значение не превосходит $p$ , то добавляем в выборку элемент, взятый из нормального распределения, иначе — элемент, взятый из равномерного).
$H_0\,:$ распределение $X$ нормально, $H_1\,:\; H_0$ неверна;
$n=10\,:\,5\,:\,100.$

Смоляков: $a=1, \;\; p=0\,:\,0.02\,:\,1.$ Сравнить критерии Шапиро-Уилка и хи-квадрат.

Целых: $a=2, \;\; p=0\,:\,0.02\,:\,1.$ Сравнить критерии Жарка-Бера и Шапиро-Уилка.

$X_1^{n_1}, \;\; X_{1i} \sim N(\mu_1, \sigma_1^2),\;\;X_2^{n_2}, \;\; X_{2i} \sim N(\mu_2, \sigma_2^2);$
$H_0\,:$ средние выборок равны, $H_1\,:$ средние выборок не равны;
$\mu_1=0, \;\; \sigma_1=1.$

Цыганова: $\mu_2=-2\,:\,0.02,\:\,2, \;\; \sigma_2 = 0.5\,:\,0.01\,:\,2, \;\; n=m=30.$ Сравнить критерий Стьюдента для неизвестных равных дисперсий и двухвыборочный перестановочный критерий.

Шпакова: $\mu_2=-2\,:\,0.02,\:\,2, \;\; \sigma_2 = 1, \;\; n=m=5\,:\,1\,:\,50.$ Сравнить критерий Аспина-Уэлша и двухвыборочный перестановочный критерий.

Задание 2. Анализ реальных данных

Ниже приведены описания анализируемых данных и постановки задач. При проведении анализа можно пользоваться любыми доступными программными средствами. Необходимо предоставить подробный письменный отчёт по проведённому исследованию, содержащий визуализацию исходных данных, описания и выводы каждого этапа анализа — используемые методы, обоснование их применимости, промежуточные результаты вычислений, графики. Особое внимание необходимо обращать на полноту применения методов. Помимо выводов, касающихся математических особенностей решения, необходимо включить в отчёт заключения, сформулированные в терминах предметной области, которые могли бы быть понятны гипотетическому заказчику-нематематику.

Отчёт каждого студента рецензируется назначенным одногруппником. Задачей рецензента является проверка корректности выбора метода решения, полноты его применения и понятности изложения. Рецензент получает баллы, если рецензируемая им работа была принята с первого раза, при условии, что его собственная работа также сдана.

Предварительные версии отчётов принимаются до 23:59 5.12, финальные, по результатам работы с рецензентом — до 23:59 15.12.

Задания

Линейные размеры тысячефранковых банкнот

Банкнота в 1000 швейцарских франков серии, действовавшей в период с 1911 по 1958. Красным обозначены измеренные величины.

Имеются данные измерений двухсот швейцарских тысячефранковых банкнот, бывших в обращении в первой половине XX века. Сто из банкнот были настоящими, и сто — поддельными. Измерены следующие величины: $X_1$ — длина банкноты, $X_2$ — ширина банкноты с левой стороны, $X_3$ — ширина банкноты с правой стороны, $X_4$ — расстояние от нижнего края до рамки рисунка, $X_5$ — расстояние от нижнего края до рамки рисунка, $X_6$ — длина диагонали рисунка.

Студент 1: построить функцию, оценивающую вероятность того, что имеющаяся банкнота фальшивая, и доверительный интервал для неё. Какие группы признаков необходимы для этого? Каков наименьший набор признаков, позволяющий достаточно надёжно выявить фальшивую купюру?

Надёжность шарикоподшипников

Мерой надёжности шарикоподшипников служит величина $L_{10}$ — максимальное число оборотов, которое выдерживает 90% одинаковых подшипников. Имеются данные измерений надёжности по шарикоподшипникам трёх производителей (для одного из производителей исследовано три вида подшипников), для каждого испытания указаны диаметр и число шаров в подшипнике, нагрузка и величина $L_{10}$ .

Студент 2: построить функцию, оценивающую $L_{10}$ по имеющимся признакам, рассчитать точность оценки.

Продолжительность жизни и активность размножения самцов дрозофилы

Для изучения влияния активности размножения самцов дрозофилы на продолжительность их жизни был организован следующий эксперимент. По 25 самцов в пяти группах содержались в одинаковых условиях, за исключением одного отличия: в первой группе к каждому самцу ежедневно подсаживалась готовая к размножению самка, во второй – восемь готовых к размножению самок, в третьей и четвёртой - соответственно, одна и восемь беременных самок, не готовых к размножению, наконец, к самцам четвёртой группы не подсаживали никого. Для каждого самца измерена продолжительность жизни, длина грудной клетки и доля времени, проводимого во сне.

Студент 3: построить функцию, предсказывающую продолжительность жизни самца дрозофилы в зависимости от условий его содержания, дать интерпретацию вклада признаков.

Электрическая прочность диэлектрика

Была измерена электрическая прочность изоляции проводов на разных сроках их эксплуатации и при различной температуре. Известно, что зависимость электрической прочности диэлектрика от времени и температуры имеет вид $\log(y)=\beta_1-\beta_2\cdot time \cdot e^{-\beta_3\cdot temperature}$ .

Студент 4: найти значения констант $\beta_1, \beta_2, \beta_3,$ построить для них доверительные области, оценить качество построенной модели.

Данные антропометрии

Некоторые из измеренных характеристик скелета.

Для 247 мужчин и 260 женщин измерены две группы антропометрических показателей – легко измеримые характеристики скелета и обхваты, всего 21 признак. Указаны возраст, пол, вес и рост.

Студент 5: построить функцию, эффективно оценивающую вес по наименьшему набору признаков; сравнить точность оценки веса при отсутствии информации по обхватам и отсутствии информации по характеристикам скелета.

Студент 6: построить функцию, оценивающую по наименьшему набору признаков вероятность того, что испытуемый — женщина, и доверительный интервал для этой вероятности.

Пожертвования на благотворительность

Благотворительная организация разослала 4268 писем с предложением сделать пожертвование и получила отклик с пожертвованиями от 1707 адресатов. Для каждого адресата известны: индикатор ответа на предыдущее письмо, число недель, прошедших с момента предыдущего пожертвования, размеры текущего, предыдущего и среднего по всем предыдущим пожертвованиям в голландских гульденах, число писем, отправляемых адресату в год, доля писем, в ответ на которые приходят пожертвования.

Студент 7: построить функцию, оценивающую вероятность получения пожертвования от адресата по историческим данным.

Студент 8: построить функцию, оценивающую вероятный размер пожертвования от адресата по историческим данным.

Влияние глифосата на рост плевел

Сравниваются два вида плевел, дикая разновидность и мутантная, выработавшая устойчивость к глифосату. Оба вида в равных пропорциях засеиваются в теплицу, проводится обработка глифосатом, по окончании эксперимента измеряются плотности зарастания (количество растений на единицу площади) дикой $x$ и мутантной $z$ разновидностей. Целевой признак $y$ - средняя биомасса дикой разновидности (в граммах на одно растение). Для него предложена следующая модель:
$y=\frac{a}{1+b\left(x+cz\right)}$ ,
где коэффициент $a$ имеет смысл гипотетической средней биомассы при нулевой плотности зарастания, $b$ – коэффициент внутривидовой конкуренции для дикой разновидности, $c$ – коэффициент взаимозаменяемости видов (если он равен единице, то виды взаимозаменяемы.

Студент 9: найти значения коэффициентов $a, b, c,$ построить для них доверительные области, оценить качество построенной модели. Можно ли сказать, что виды взаимозаменяемы?

Пассажиры Титаника

Приведены данные о 1309 пассажирах Титаника. Для каждого пассажира указано имя, пол, возраст, класс и цена билета, число родственников на борту, и, кроме того, удалось ли ему выжить.

Студент 10: построить функцию, предсказывающую вероятность выживания пассажира по имеющимся данным, оценить точность предсказания.

Литература

Кобзарь А. И. Прикладная математическая статистика. — М.: Физматлит, 2006.

Ссылки

Источник — «http://machinelearning.ru/wiki/index.php?title=%D0%A1%D1%82%D0%B0%D1%82%D0%B8%D1%81%D1%82%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D0%B9_%D0%B0%D0%BD%D0%B0%D0%BB%D0%B8%D0%B7_%D0%B4%D0%B0%D0%BD%D0%BD%D1%8B%D1%85_%28%D0%BA%D1%83%D1%80%D1%81_%D0%BB%D0%B5%D0%BA%D1%86%D0%B8%D0%B9%2C_%D0%9A.%D0%92.%D0%92%D0%BE%D1%80%D0%BE%D0%BD%D1%86%D0%BE%D0%B2%29/2013%2C_%D0%A4%D0%A3%D0%9F%D0%9C»

Категория: Учебные курсы

Статистический анализ данных (курс лекций, К.В.Воронцов)/2013, ФУПМ

Материал из MachineLearning.

Содержание

Оценки

Задание 1. Исследование свойств одномерных статистических критериев на модельных данных

Пример задания

Задания

Анализ поведения схожих критериев

Задание 2. Анализ реальных данных

Задания

Линейные размеры тысячефранковых банкнот

Надёжность шарикоподшипников

Продолжительность жизни и активность размножения самцов дрозофилы

Электрическая прочность диэлектрика

Данные антропометрии

Пожертвования на благотворительность

Влияние глифосата на рост плевел

Пассажиры Титаника

Литература

Ссылки

Просмотры

Личные инструменты

Навигация

Поиск

Инструменты