Тригонометрическая интерполяция

Материал из MachineLearning.

(Различия между версиями)
Перейти к: навигация, поиск
(→Дискретное преобразование Фурье)
Текущая версия (16:57, 17 декабря 2008) (править) (отменить)
(→Список литературы)
 
(28 промежуточных версий не показаны.)
Строка 1: Строка 1:
 +
==Постановка задачи==
 +
Интерполяция - приблежение одной функции с помощью другой. Это может понадобиться в случае, когда вычислительно сложную функцию нужно заменить более легкой. Есть много видов метода интерполяции и способов их применения. Здесть мы рассмотрим особый вид интерполяции - тригонометрическую. На класс функций, при которых ее удобно использовать накладывается сильное ограничение - они должны быть периодическими, но более подробно об этом ниже.
 +
 +
Для использования математических формул для тригонометрической интерполяцией необходимо ознакомиться с теорией дискретного преобразования Фурье.
 +
==Дискретное преобразование Фурье==
==Дискретное преобразование Фурье==
-
В прикладных задачах часто используются различные преобразования Фурье функций непрерывного аргументся, а также представлений функций с помощью сходящихся тригонометрических рядов.
+
В прикладных задачах часто используются различные преобразования Фурье функций непрерывного аргумента, а также представлений функций с помощью сходящихся тригонометрических рядов.
-
Всякую непрерывно дифференцируемую фцнкцию <tex>f</tex> можно разложить в ряд Фурье:
+
Всякую непрерывно дифференцируемую функцию <tex>f</tex> можно разложить в ряд Фурье:
<tex>f(x)=\sum_{k=-\infty}^{\infty} \alpha_k exp{2\pi i k x}</tex>
<tex>f(x)=\sum_{k=-\infty}^{\infty} \alpha_k exp{2\pi i k x}</tex>
-
коэффициенты <tex>\alpha_k</tex> находятся по следущим формулам
+
коэффициенты <tex>\alpha_k</tex> находятся по следующим формулам
<tex>\alpha_k=\int \limits_{0}^{1} f(x) exp {-2 \pi i k x} dx</tex>
<tex>\alpha_k=\int \limits_{0}^{1} f(x) exp {-2 \pi i k x} dx</tex>
-
Но как правила функция задана только в некоторых точках или у нас есть возможность узнать ее значения только в некотором конечном числе точек. Допустим, <tex> x_j=j/N, j=0,1,\dots,N-1 </tex>.В этом случае аналогом функции непрервной интерполяции функции будет дискретный вариант:
+
Но как правила функция задана только в некоторых точках или у нас есть возможность узнать её значения только в некотором конечном числе точек. Допустим, <tex> x_j=j/N, j=0,1,\dots,N-1 </tex>.В этом случае аналогом функции непрерывной интерполяции функции будет дискретный вариант:
<tex> f(x_j)=\sum_{k=0}^{N-1} \alpha_k exp{2\pi ikx_j}, 0\le j<N </tex>
<tex> f(x_j)=\sum_{k=0}^{N-1} \alpha_k exp{2\pi ikx_j}, 0\le j<N </tex>
-
Разложение имеет место когда функцию можно приблизить тригонометрическим многочленом следущего вида в заданных нам точках
+
Разложение имеет место когда функцию можно приблизить тригонометрическим многочленом следующего вида в заданных нам точках
<tex>S_N(x)=\sum_{k=0}^{N-1}a_k exp{2 \pi ikx} </tex>
<tex>S_N(x)=\sum_{k=0}^{N-1}a_k exp{2 \pi ikx} </tex>
Строка 23: Строка 28:
Далее для удобства записи будем использовать <tex>\omega=exp{2\pi i/N}</tex>
Далее для удобства записи будем использовать <tex>\omega=exp{2\pi i/N}</tex>
-
Часто используется следущий вид формул:
+
Часто используется следующий вид формул:
-
<tex> f(x_j)=\sum_{-N/2<k\le N/2} a_k exp{2\pi ikx_j}, </tex> и это соответсвует интерполяции тригонометрическим многочленом
+
<tex> f(x_j)=\sum_{-N/2<k\le N/2} a_k exp{2\pi ikx_j}, </tex> и это соответствует интерполяции тригонометрическим многочленом
-
<tex>S_N=\sum{-N/2<k\le N/2}a_k exp{2\pi i kx}</tex>, где коэффициенты <tex>a_k</tex> считаются по тем же формулам.
+
-
Если вычисления проводить по вышеприведенноым формулам, то на выполнения каждого из преобразований потребуется <tex>N^2</tex> арифметических операций (считаем, что <tex>\omega=exp{2\pi i/N}</tex> уже вычислены). Если N не является простым числом, то количество операций можно значительно сократить, используя [[быстрое преобразование Фурье]].
+
<tex>S_N=\sum_{-N/2<k\le N/2}a_k exp{2\pi i kx}</tex>,
 +
 
 +
где коэффициенты <tex>a_k</tex> считаются по тем же формулам.
 +
 
 +
Если вычисления проводить по вышеприведённым формулам, то на выполнения каждого из преобразований потребуется <tex>N^2</tex> арифметических операций (считаем, что <tex>\omega=exp{2\pi i/N}</tex> уже вычислены). Если N не является простым числом, то количество операций можно значительно сократить, используя [[быстрое преобразование Фурье]].
==Пример использования==
==Пример использования==
-
Рассмотрим применение тригонметрической интерполяции.
+
Рассмотрим применение тригонометрической интерполяции.
-
Будем использовать для приблежения следущий тригонометрический полином:
+
Будем использовать для приближения следующий тригонометрический полином:
-
<tex>\begin{matrix} f_n(x)=a_0 &amp; + &amp; a_1 \cos x + a_2 \cos 2x+\dots + a_n \cos nx + \\ \ &amp;+&amp;b_1 \sin x + b_2 \sin 2x+\dots + b_n \sin nx . \end{matrix}</tex>
+
<tex>\begin{matrix} F_n(x)=a_0 &amp; + &amp; a_1 \cos x + a_2 \cos 2x+\dots + a_n \cos nx + \\ \ &amp;+&amp;b_1 \sin x + b_2 \sin 2x+\dots + b_n \sin nx . \end{matrix}</tex>
 +
 
 +
Будем искать приближение функции f(x). Пусть известно значения <tex>f(\frac{2\pi j}{2n+1})=y_i</tex> при <tex>j\in \{-n,-n+1,\dots,0,1,\dots n\}</tex>
 +
 
 +
Тогда по формулам изложенным выше можно получить
 +
<tex>
 +
a_m= \frac{2}{2n+1} \sum_{j=-n}^n y_j \cos \left( \frac{2\pi jm}{2n+1} \right),\quad b_m= \frac{2}{2n+1} \sum_{j=-n}^n y_j \sin \left(\frac{2\pi jm}{2n+1} \right) </tex>
 +
 
 +
Если интерполировать тригонометические функции и выбирать правильное число узлов, то погрешность приближается к нулю. Интересно рассмотреть функции, не являющиеся тригонометрическими, но обладающие периодом. Рассмотрим ряд вычислений приближенных функций с помощью программы, использующей выше изложенный алгоритм апроксимации.
 +
На вход подается функция и количество точек на промежутке <tex>[-\pi;\pi]</tex>, точки по умолчанию расположены равномерно на промежутке. Как будет показано ниже, это соответсвует наилучшей аппроксимации.
 +
 
 +
Тригонометрическая функция с шумом
 +
 
 +
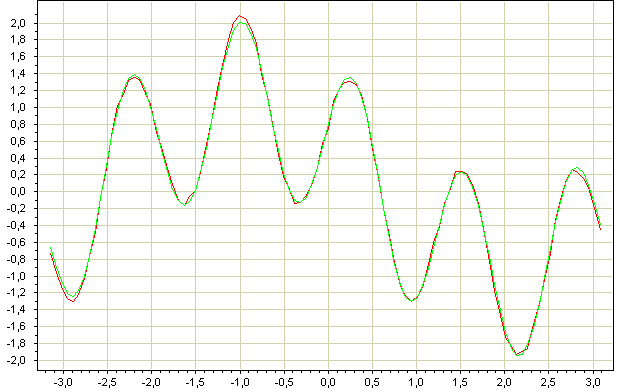
На вход подавалась функция <tex>sin(5*x)+cos(x)+rand()</tex>, (пусть под 'rand()' понимается некоторая шумовая функция).
 +
Вычислияем значение функции в 5 точках. По графику ('Рис.1')видно, что аппроксимация произвендена достаточно точно.
 +
 
 +
[[Изображение:Slide1.gif|||Рис.1]]
 +
 
 +
Выход : коэффициенты <tex>a_n, b_n</tex>, чтоб можно было восстановить многочлен с помощью других вычислительных инструментов.
 +
Также ряд значений функции на промежутке <tex>[-\pi,\pi]</tex>. Количество точек запрашивается у пользователя.
 +
 
 +
Не тригонометрическая кусочно-заданная функция
 +
 
 +
Попробуем приблизить кусочно-заданную функцию с помощью тригонометрической интерполяций, зная ее значения в конечном числе точек. (Такую функцию можно разложить точно, используя обычное преобразование Фурье). При тригонометрической интерполяции строится многочлен, число тригонометрических функций которого определяется числом узлов интерполяции. Таким образом, чем больше мы возьмем точек интерполяции мы возьмем, тем лучще мы приблизимся к виду разложения Фурье.
 +
 
 +
[[Изображение:kusochnozadannaya.png|||Рис.2]]
 +
 
 +
На вход программе подавалась кусочно-заданная функция <tex> \pi<x<-1.5 y=1, -1.5<x<1.6 y=0, 1.6<x<\pi </tex>, функция подразумевается периодической с периодом <tex>\pi</tex>. Для вычисления полинома бралось 25 точек. На Рис.2 приведен график функциии и график интерполирующего полинома. На Рис.4 приведен график ошибки интерполяции.
 +
 
 +
[[Изображение:Error1.png|||Рис.3]]
 +
 +
Как видно из графика функции ошибки она максимальна на а районе концлв промежутка.
==Погрешность вычислений==
==Погрешность вычислений==
 +
Для минимизации погрешность вычислений в методе тригонометрической интерполяции лучше всего использовать узлы Чебышева.
-
==Пример использования==
+
==Программная реализация==
 +
В данной программной реализации функция занесена в код программы, по этому в исполняемом файле не может быть изменена. Но при необходимости можно править код С++ и реализовывать необходимые функции.
 +
 
 +
[[Media:Trigonometric interpolation.zip|Реализация программы на языке С++]]
 +
 
 +
[[Media:Text_trig.zip|Код программы на языке С++]]
==Список литературы==
==Список литературы==
 +
 +
* ''А.А.Самарский, А.В.Гулин.''&nbsp; Численные методы М.: Наука, 1989.
 +
* ''А.А.Самарский.''&nbsp; Введение в численные методы М.: Наука, 1982.
 +
 +
== См. также ==
 +
* [[Интерполяция каноническим полиномом]]
 +
* [[Рациональная интерполяция]]
 +
* [[Интерполяция функций двух переменных, проблема выбора узлов | Проблема выбора узлов для интерполяции]]
 +
* [[Практикум ММП ВМК, 4й курс, осень 2008]]
 +
 +
 +
{{Заготовка}}
 +
[[Категория:Учебные задачи]]

Текущая версия

Содержание

Постановка задачи

Интерполяция - приблежение одной функции с помощью другой. Это может понадобиться в случае, когда вычислительно сложную функцию нужно заменить более легкой. Есть много видов метода интерполяции и способов их применения. Здесть мы рассмотрим особый вид интерполяции - тригонометрическую. На класс функций, при которых ее удобно использовать накладывается сильное ограничение - они должны быть периодическими, но более подробно об этом ниже.

Для использования математических формул для тригонометрической интерполяцией необходимо ознакомиться с теорией дискретного преобразования Фурье.

Дискретное преобразование Фурье

В прикладных задачах часто используются различные преобразования Фурье функций непрерывного аргумента, а также представлений функций с помощью сходящихся тригонометрических рядов. Всякую непрерывно дифференцируемую функцию f можно разложить в ряд Фурье:

f(x)=\sum_{k=-\infty}^{\infty} \alpha_k exp{2\pi i k x}

коэффициенты \alpha_k находятся по следующим формулам

\alpha_k=\int \limits_{0}^{1} f(x) exp {-2 \pi i k x} dx

Но как правила функция задана только в некоторых точках или у нас есть возможность узнать её значения только в некотором конечном числе точек. Допустим, x_j=j/N, j=0,1,\dots,N-1 .В этом случае аналогом функции непрерывной интерполяции функции будет дискретный вариант:

f(x_j)=\sum_{k=0}^{N-1} \alpha_k exp{2\pi ikx_j}, 0\le j<N

Разложение имеет место когда функцию можно приблизить тригонометрическим многочленом следующего вида в заданных нам точках

S_N(x)=\sum_{k=0}^{N-1}a_k exp{2 \pi ikx}

Система функций \phi (x)=2\pi kx, 0\le k <N является ортогональной, на множестве точек x_j=j/N, 0\le j<N при том что (\phi_k,\phi_k)=N, таким образом разложение имеет место и коэффициенты a_k представляются в виде:

a_k=\frac{1}{N} \sum_{l=0}^{N-1} f(x_l)exp{-2\pi ikx_l}, 0\le k<N

Далее для удобства записи будем использовать \omega=exp{2\pi i/N}

Часто используется следующий вид формул:

f(x_j)=\sum_{-N/2<k\le N/2} a_k exp{2\pi ikx_j}, и это соответствует интерполяции тригонометрическим многочленом

S_N=\sum_{-N/2<k\le N/2}a_k exp{2\pi i kx},

где коэффициенты a_k считаются по тем же формулам.

Если вычисления проводить по вышеприведённым формулам, то на выполнения каждого из преобразований потребуется N^2 арифметических операций (считаем, что \omega=exp{2\pi i/N} уже вычислены). Если N не является простым числом, то количество операций можно значительно сократить, используя быстрое преобразование Фурье.

Пример использования

Рассмотрим применение тригонометрической интерполяции. Будем использовать для приближения следующий тригонометрический полином:

\begin{matrix} F_n(x)=a_0 & + & a_1 \cos x + a_2 \cos 2x+\dots + a_n \cos nx + \\ \ &+&b_1 \sin x + b_2 \sin 2x+\dots + b_n \sin nx . \end{matrix}

Будем искать приближение функции f(x). Пусть известно значения f(\frac{2\pi j}{2n+1})=y_i при j\in \{-n,-n+1,\dots,0,1,\dots n\}

Тогда по формулам изложенным выше можно получить a_m= \frac{2}{2n+1} \sum_{j=-n}^n y_j \cos \left( \frac{2\pi jm}{2n+1} \right),\quad b_m= \frac{2}{2n+1} \sum_{j=-n}^n y_j \sin \left(\frac{2\pi jm}{2n+1} \right)

Если интерполировать тригонометические функции и выбирать правильное число узлов, то погрешность приближается к нулю. Интересно рассмотреть функции, не являющиеся тригонометрическими, но обладающие периодом. Рассмотрим ряд вычислений приближенных функций с помощью программы, использующей выше изложенный алгоритм апроксимации. На вход подается функция и количество точек на промежутке [-\pi;\pi], точки по умолчанию расположены равномерно на промежутке. Как будет показано ниже, это соответсвует наилучшей аппроксимации. 

Тригонометрическая функция с шумом

На вход подавалась функция sin(5*x)+cos(x)+rand(), (пусть под 'rand()' понимается некоторая шумовая функция). Вычислияем значение функции в 5 точках. По графику ('Рис.1')видно, что аппроксимация произвендена достаточно точно.

Рис.1

Выход : коэффициенты a_n, b_n, чтоб можно было восстановить многочлен с помощью других вычислительных инструментов. Также ряд значений функции на промежутке [-\pi,\pi]. Количество точек запрашивается у пользователя. 

Не тригонометрическая кусочно-заданная функция

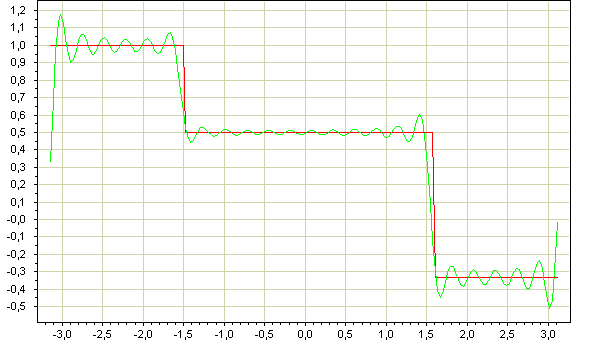
Попробуем приблизить кусочно-заданную функцию с помощью тригонометрической интерполяций, зная ее значения в конечном числе точек. (Такую функцию можно разложить точно, используя обычное преобразование Фурье). При тригонометрической интерполяции строится многочлен, число тригонометрических функций которого определяется числом узлов интерполяции. Таким образом, чем больше мы возьмем точек интерполяции мы возьмем, тем лучще мы приблизимся к виду разложения Фурье.

Рис.2

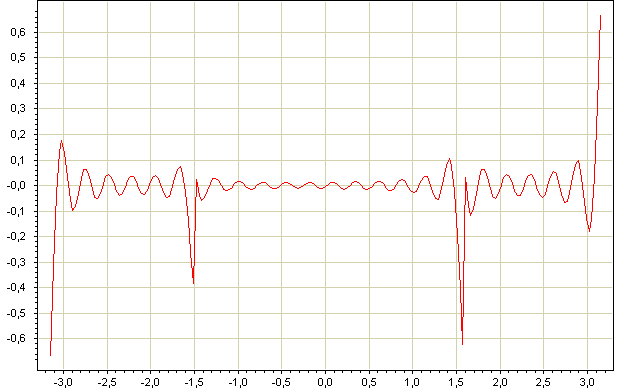
На вход программе подавалась кусочно-заданная функция \pi<x<-1.5 y=1, -1.5<x<1.6 y=0, 1.6<x<\pi , функция подразумевается периодической с периодом \pi. Для вычисления полинома бралось 25 точек. На Рис.2 приведен график функциии и график интерполирующего полинома. На Рис.4 приведен график ошибки интерполяции.

Рис.3

Как видно из графика функции ошибки она максимальна на а районе концлв промежутка.

Погрешность вычислений

Для минимизации погрешность вычислений в методе тригонометрической интерполяции лучше всего использовать узлы Чебышева.

Программная реализация

В данной программной реализации функция занесена в код программы, по этому в исполняемом файле не может быть изменена. Но при необходимости можно править код С++ и реализовывать необходимые функции.

Реализация программы на языке С++

Код программы на языке С++

Список литературы

  • А.А.Самарский, А.В.Гулин.  Численные методы М.: Наука, 1989.
  • А.А.Самарский.  Введение в численные методы М.: Наука, 1982.

См. также


Источник — «http://machinelearning.ru/wiki/index.php?title=%D0%A2%D1%80%D0%B8%D0%B3%D0%BE%D0%BD%D0%BE%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B0%D1%8F_%D0%B8%D0%BD%D1%82%D0%B5%D1%80%D0%BF%D0%BE%D0%BB%D1%8F%D1%86%D0%B8%D1%8F»
Личные инструменты