Эмпирическое распределение
Материал из MachineLearning.
(Новая: '''Эмпирическая функция распределения''' — естественное приближение теоретической [[Функция распреде...) |
|||
| Строка 3: | Строка 3: | ||
== Определения == | == Определения == | ||
| + | Пусть задана [[Выборка|случайная выборка]] <tex>x^m=\left(x_1,\ldots,x_m\right)</tex> наблюдений <tex>x_i \in X.</tex> | ||
| + | Построим по выборке ступенчатую функцию <tex>\hat{F}_m(x)</tex>, возрастающую скачками величины <tex>\frac{1}{m}</tex> в точках <tex>x_{(i)}.</tex> | ||
| + | Построенная функция называется ''эмпирической функцией распределения''. | ||
| + | Для задания значений в точках разрыва формально определим её так: | ||
| + | ::<tex>\hat{F}_m(x)\;=\;\frac{1}{m}\sum_{i=1}^m I_{\left\{x_i\leq x\right\}}.</tex> | ||
| + | |||
| + | '''Замечание:''' при этом эмпирическая функция непрерывна справа. | ||
| + | |||
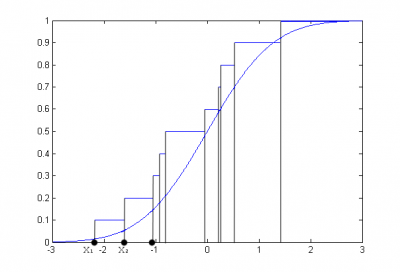
| + | На рисунке представлена функция стандартного нормального распределения и эмпирическая функция распределения, построенная по выборке из 10 случайных наблюдений из стандартного нормального закона. | ||
| + | |||
| + | [[Изображение:EmpCdf.png|thumb|right|400px|Пример эмпирической функции распределения, построенной по выборке из 10 наблюдений.]] | ||
| + | |||
| + | ==Свойства эмпирической функции распределения== | ||
| + | === Эмпирическое распределение для фиксированного <tex>x</tex> === | ||
| + | |||
| + | Поскольку случайная величина <tex>I_{\left\{x_i\leq x\right\}}</tex> имеет распределение Бернулли с вероятностью успеха <tex>F(x)</tex> (где <tex>F(x)</tex> - теоретическая | ||
| + | [[Функция распределения|функция распределения]] случайной величины <tex>x</tex>), а последовательность <tex>\left(I_{\left\{x_1\leq x\right\}},\ldots,I_{\left\{x_m\leq x\right\}}\right)</tex> - схема Бернулли с вероятностью успеха <tex>F(x)</tex>, то по отношению к этой последовательности <tex>\hat{F}_m(x)</tex> есть частота попаданий левее x. | ||
| + | |||
| + | ===Математическое ожидание и дисперсия эмпирического распределения=== | ||
| + | Математическое ожидание эмпирической функции распределения | ||
| + | *<tex>E\left[\hat{F}_m(x)\right] = F(x),</tex> | ||
| + | |||
| + | таким образом эмпирическое распределение является [[Несмещённая оценка|несмещённой оценкой]] теоретической функции распределения <tex>F(x)</tex>. | ||
| + | |||
| + | Дисперсия эмпирического распределения | ||
| + | *<tex>D\left[\hat{F}_m(x)\right]=\frac{F(x)\left(1-F(x)\right)}{m}.</tex> | ||
| + | |||
| + | ===Асимптотические свойства эмпирической функции распределения=== | ||
| + | |||
| + | # По [[Закон больших чисел|усиленному закону больших чисел]] <tex>\hat{F}_m(x)</tex> сходится ''почти наверное'' к теоретической функции распределения <tex>F(x).</tex> | ||
== Замечания == | == Замечания == | ||
Версия 12:23, 6 января 2010
Эмпирическая функция распределения — естественное приближение теоретической функции распределения данной случайной величины, построенное по выборке.
Содержание |
Определения
Пусть задана случайная выборка наблюдений
Построим по выборке ступенчатую функцию
, возрастающую скачками величины
в точках
Построенная функция называется эмпирической функцией распределения.
Для задания значений в точках разрыва формально определим её так:
Замечание: при этом эмпирическая функция непрерывна справа.
На рисунке представлена функция стандартного нормального распределения и эмпирическая функция распределения, построенная по выборке из 10 случайных наблюдений из стандартного нормального закона.
Свойства эмпирической функции распределения
Эмпирическое распределение для фиксированного 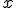
Поскольку случайная величина имеет распределение Бернулли с вероятностью успеха
(где
- теоретическая
функция распределения случайной величины
), а последовательность
- схема Бернулли с вероятностью успеха
, то по отношению к этой последовательности
есть частота попаданий левее x.
Математическое ожидание и дисперсия эмпирического распределения
Математическое ожидание эмпирической функции распределения
таким образом эмпирическое распределение является несмещённой оценкой теоретической функции распределения .
Дисперсия эмпирического распределения
Асимптотические свойства эмпирической функции распределения
- По усиленному закону больших чисел
сходится почти наверное к теоретической функции распределения