Оценка сложности регрессионных моделей (пример)

Материал из MachineLearning.

(Различия между версиями)

Версия 19:05, 15 декабря 2010

Задача восстановления регрессии является частным случаем задачи обучения по прецедентам. При выборе модели, как и для всех задач обучения по прецедентам, возможны проблемы недообучения и переобучения.

В случае недообучения, модель недостаточно сложна для описания данных с требуемой точностью. А в случае переобучения, возникающего при избыточной сложности моделей, средняя ошибка на тестовой выборке существенно выше,чем на обучающей выборке.

Таким образом, для каждой задачи существует оптимальная сложность модели.

Содержание

1 Способы оценки сложности регрессионных моделей
2 Постановка задачи
3 Численный эксперимент
- 3.1 Модели с оптимальным количеством параметров, недообученная и переобученная
4 Литература

Способы оценки сложности регрессионных моделей

Существуют различные способы оценки сложности, используемые при выборе регрессионных моделей. Одним из них является критерий Акаике (AIC), основанный на принципе Оккама, а также тесно связанный с ним Байесовский информационный критерий (BIC). В теории Вапника-Червоненкиса одним из ключевых понятий является размерность Вапника-Червоненкиса, которая также является характеристикой сложности семейства алгоритмов.

Поскольку задача описания данных формально эквивалентна кодированию, то сложность модели можно оценивать также как длину требуемого для её описания кода. На этом основан принцип минимальной длинны описания (MDL)^[1] ^[1].

Функция правдоподобия (достоверность) в некотором роде тоже можно рассматривать как оценку сложности модели^[1].

Постановка задачи

Рассматривается линейная регрессионная модель

$y= f(\mathbf{w},\mathbf{x}) + \nu= \sum^W_{j=1}w_jf_j(\mathbf{x})+\nu$

Предполагается, что случайная величина распределена нормально с нулевым матожиданием и фиксированной дисперсией $\sigma^2$ , которая не зависит от переменных $x, y$ . При таких предположениях параметры $\mathbf{w}$ регрессионной модели вычисляются с помощью метода наименьших квадратов.

Будем рассматривать одномерные выборки. Обозначим порождаемые признаки $a_j=g_j(x)$ (свободные переменные).

Множество порождающих функций $G=\{1, x^{\frac{1}{2}}, x, x^{\frac{3}{2}}, x^2, tgx, lnx, e^x\}$

В качестве модели, описывающей отношение между свободными переменными $a_j$ и зависимой переменной $y$ будем использовать полином Колмогорова-Габора

$y=w_0+\sum^{|G|}_{i=1}w_ia_i+\sum^{|G|}_{i=1}\sum^{|G|}_{j=1}w_{ij}a_ia_j+\ldots+\sum^{|G|}_{i=1}\ldots\sum^{|G|}_{z=1}w_{ij\ldots z}a_ia_j\ldots a_z +\ldots$

Где вектор коэффициентов $w=(w_0,w_i,w_{ij},\ldots)_{i,j,\ldots=1,2,\ldots}$

Используя модельные данные, мы будем строить кривые зависимости AIC, BIC, размерности Вапника-Червоненкиса, длинны описания(MDL), функции правдоподобия (достоверности), а также количества хорошо определяемых параметров от количества мономов полинома Колмлгорова-Габора, с целью сравнить оптимальное по различным критериям количество признаков.

Вычисление AIC и BIC для линейной регрессионной модели

Пусть: $X = \{x_i\}^{n}_{i=1}$ - наблюдаемая часть выборки, где каждый объект характеризуется набором параметров $x_i=(x_{i_1},...,x_{i_k})$ .

$SSE=\|f(x_i)-y_i\|_2=\sum_{i=1}^n(y_i-f(w,x_i))^2$ ;

$\sigma^2=\frac{SSE}{n-2}$ — дисперсия остатков;

В случае линейной регрессионной модели критерий BIC выражается через SSE (Sum of Squared Errors) - сумму квадратов остатков - и $\sigma^2$ - дисперсия остатков. $BIC=n\[\ln(\sigma^2)\]+k\ln(n)$

А критерий Акаике через SSE. $k$ - число параметров модели

$AIC = 2k+n\[\ln(\sigma^2)\]$

Лучшая модель соответствует минимальному значению критерия.

Вычисление размерности Вапника-Червоненкиса

Если существует число $h$ такое, что функция роста $\Delta A(h) = 2^h$ и $\Delta A(h+1) < 2^{h+1}$ , то оно называется ёмкостью или размерностью Вапника-Червоненкиса (VC-dimension) семейства алгоритмов $A$ . Если такого числа $h$ не существует, то говорят, что семейство $A$ имеет бесконечную ёмкость.

Другая формулировка определения (через разнообразие): Пусть задано множество объектов $X$ и некоторое семейство функций (алгоритмов классификации, решающих правил) $A$ , которые сопоставляют каждому объекту множества $X$ один из двух заданных классов. Ёмкостью семейства $A$ называется наибольшее число $h$ , такое, что существует подмножество из $h$ объектов в множестве $X$ , которое функции из $A$ могут разбить на два класса всеми возможными способами. Если же такие подмножества существуют для сколь угодно большого $h$ , то ёмкость полагается равной бесконечности.

Для задач регрессии обычно размерность Вапника-Червоненкиса принимают равной количеству параметров $k$ .

Вычисление функции правдоподобия и количества хорошо определяемых параметров

Для оценки сложности используется логарифм функции правдоподобия(evidence)

$ln p(D|\beta, A)=-\frac{1}{2}ln|A|-\frac{N}{2}ln2\pi+\frac{N}{2}ln\beta-S(w_0)-\frac{1}{2}ln|H|$

Где $E_D$ функция регрессионных невязок:

$E_D=\frac{1}{2}\sum^n_{i=1}(f(x_i)-y_i)^2$

Функция ошибки:

$S(w)=\frac{1}{3}w^TAw+\beta E_D$

Матрица Гессе функции ошибок

$H=-\nabla\nabla S(w)|_{w=w_0}$

Представим $A=I_W||\frac{1}{a}||$

$H_D$ части Гессеана, не зависящие от $A$

Количество хорошо определяемых параметров:

$\gamma=\sum^W_{j=1}\frac{\lambda_j}{\lambda_j+a_j}$

Численный эксперимент

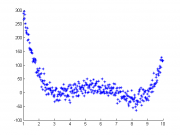
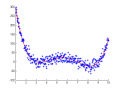
Генерация модельных данных.

Функция - полином 4й степени. Случайная составляющая нормально распределена.

x=1:.025:10;
y=(x-3).*(x-4).*(x-7).*(x-9)+15.*randn(size(x));
scatter(x,y,'*')
% запишем x и y в виде столбцов
x=x';
y=y';

Порождение признаков

%Построим матрицу подстановок (В модели будем использовать полином Колмогорова-Габора до третьей
%степени от попрождающих функций)
Ap=[ x.^0,x.^0.5,x,x.^1.5,x.^2, tan(x),log(x),exp(x) ]; %Полином первой степени
%добавим столбцы, соответствующие полиному второй степени
for i=5:8,
    for j=2:5,
        Ap(:,size(Ap,2)+1)=Ap(:,i).*Ap(:,j);
    end
end
for i=6:8,
    for j=i:8,
        Ap(:,size(Ap,2)+1)=Ap(:,i).*Ap(:,j);
    end
end
%добавим столбцы, соответствующие третьей степени полинома
%Колмогорова-Габора
for i=12:30,
    for j=2:5,
        Ap(:,size(Ap,2)+1)=Ap(:,i).*Ap(:,j);
    end
end
for i=6:8,
    for j=i:8,
        for k=j:8,
            Ap(:,size(Ap,2)+1)=Ap(:,i).*Ap(:,j).*Ap(:,k);
        end
    end
end

Подсчет SSE, AIC и BIC

SSEcount=zeros(size(Ap,2),1);
BIC=zeros(size(Ap,2),1);
AIC=zeros(size(Ap,2),1);
 
for i=1:size(Ap,2), % цикл по количеству признаков
    w=pinv(Ap(:,1:i)'*Ap(:,1:i))*(Ap(:,1:i)')*y;
    y1=Ap(:,1:i)*w;
    plot(x,y1,'r',x,y,'*');
    r=y-y1;
    SSEcount(i) = r'*r;
    BIC(i)=i*log(size(x,1))+size(x,1)*log(SSEcount(i)*(size(x,1)-2));
    AIC(i)=2*i+size(x,1)*log(SSEcount(i)*(size(x,1)-2));
end

Вычисление функции правдоподобия и количества хорошо определяемых параметров

xRegression=Ap;
yRegression=y;
Gam=zeros(size(Ap,2),1);
 
[n,m] = size(xRegression);
 
for j = 1:m
activeSet = 1:j; % количество активных признаков
 
[weightM,alphaM,beta,weightH,alphaMH,betaH,gammaH] = ...
    getLinParam(xRegression,yRegression,activeSet);
Gam(j)=gammaH(size(gammaH,2));
[ evid(j) ] = getEvid( xRegression(:, 1:j),yRegression,weightM,alphaM,beta );
 
end

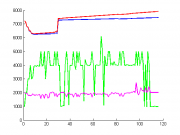
На одном графике выведем зависимость численного значения критериев от количества признаков

hold on;
plot(1:size(AIC,1),AIC,'LineWidth',2,'Color','b')
plot(1:size(AIC,1),BIC,'LineWidth',2,'Color','r')
plot(1:size(AIC,1),1000*Gam,'LineWidth',2,'Color','g')
plot(1:size(AIC,1),-evid','LineWidth',2,'Color','m')
hold off;

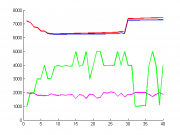
Из графика видно, что нас интересует только модели с количеством признаков не более 40

hold on;
plot(1:40,AIC(1:40),'LineWidth',2,'Color','b')
plot(1:40,BIC(1:40),'LineWidth',2,'Color','r')
plot(1:40,1000*Gam(1:40),'LineWidth',2,'Color','g')
plot(1:40,-(evid(1:40))','LineWidth',2,'Color','m')
hold off;

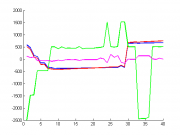
Вычтем среднее значение, чтобы были лучше видны закономерности.

hold on;
plot(1:40,AIC(1:40)-mean(AIC(1:40)),'LineWidth',2,'Color','b')
plot(1:40,BIC(1:40)-mean(BIC(1:40)),'LineWidth',2,'Color','r')
plot(1:40,1000*Gam(1:40)-mean(1000*Gam(1:40)),'LineWidth',2,'Color','g')
plot(1:40,-(evid(1:40))'-mean(-(evid(1:40))'),'LineWidth',2,'Color','m')
hold off;

Модели с оптимальным количеством параметров, недообученная и переобученная

модель с оптимальным количеством параметров k=15

Литература

Источник — «http://machinelearning.ru/wiki/index.php?title=%D0%9E%D1%86%D0%B5%D0%BD%D0%BA%D0%B0_%D1%81%D0%BB%D0%BE%D0%B6%D0%BD%D0%BE%D1%81%D1%82%D0%B8_%D1%80%D0%B5%D0%B3%D1%80%D0%B5%D1%81%D1%81%D0%B8%D0%BE%D0%BD%D0%BD%D1%8B%D1%85_%D0%BC%D0%BE%D0%B4%D0%B5%D0%BB%D0%B5%D0%B9_%28%D0%BF%D1%80%D0%B8%D0%BC%D0%B5%D1%80%29»

@@ Строка 230: / Строка 230: @@
 hold off;
 </source>
-=== Иллюстрация модели с оптимальным количеством параметров, недообученной и переобученной ===
+=== Модели с оптимальным количеством параметров, недообученная и переобученная ===
 <gallery>
-Файл:Goodmodel.png|модель с оптимальным количеством параметров k=15
+Изображение:Goodmodel.png|модель с оптимальным количеством параметров k=15
 </gallery>
 == Литература ==
 {{список примечаний}}