Критерий Краскела-Уоллиса

Материал из MachineLearning.

(Различия между версиями)

Текущая версия

Критерий Краскела-Уоллиса предназначен для проверки равенства средних нескольких выборок. Данный критерий является многовыборочным обобщением критерия Уилкоксона-Манна-Уитни. Критерий Краскела-Уоллиса является ранговым, поэтому он инвариантен по отношению к любому монотонному преобразованию шкалы измерения. Известен так же под названиями: критерий Крускала-Уоллиса, H-критерий Краскела-Уоллиса, Kruskal-Wallis one-way analysis of variance, Kruskal-Wallis test.

Содержание

1 Примеры задач
2 Описание критерия
- 2.1 Аппроксимация Краскела-Уоллиса
- 2.2 Аппроксимация Имана-Давенпорта
3 Критические значения критерия Краскела-Уоллиса при k<=5, n<=8
4 Критические значения критерия Краскела-Уоллиса при k<=6, n<=8
5 См. также
6 Литература
7 Ссылки

Примеры задач

Пример 1. Проходит чемпионат мира по футболу. Первая выборка — опрос болельщиков с вопросом "Каковы шансы на победу сборной России?" до начала чемпионата. Вторая выборка — после первой игры, третья — после второго матча и т.д. Значения в выборках — шансы России на победу по десятибальной шкале (1 — никаких перспектив, 10 — отвезти в Россию кубок — дело времени). Требуется проверить, зависят ли результаты опросов от хода чемпионата.

Пример 2. Выборка состоит из пациентов, у которых был диагностирован неизлечимый рак какого-либо органа. Всем им в качестве поддерживающей терапии был назначен к приёму витамин C (считалось, что он может способствовать выздоровлению раковых больных). Приведены данные об остаточной продолжительности жизни пациентов в днях. То есть выборка состоит из пар вида (пораженный орган, число дней), разделяясь на несколько числовых подвыборок, каждая из которых соответствует своему пораженному органу.

Требуется проверить, отличается ли остаточная продолжительность жизни в зависимости от того, какой орган поражён раковой опухолью.

Описание критерия

Заданы k выборок: $X_1=\left\{x_1^1,\dots,x_1^{n_1}\right\}, \dots, X_k=\left\{x_k^1,\dots,x_k^{n_k}\right\}$ . Объединённая выборка: $X=X_1\cup X_2\cup \dots \cup X_k$ .

Дополнительные предположения:

все k выборок простые, объединённая выборка независима;
выборки взяты из неизвестных непрерывных распределений $F_1(x),\dots,F_k(x)$ .

Проверяется нулевая гипотеза $H_0:\; F_1(x)=\dots=F_k(x)$ при альтернативе $H_1:\; F_1(x)=F_2(x-\Delta_1)=\dots=F_k(x-\Delta_{k-1})$ .

Упорядочим все $N=\sum_{i=1}^k n_i$ элементов выборок по возрастанию и обозначим $R_i^j$ ранг j-го элемента i-й выборки в полученном вариационном ряду.

Статистика критерия Краскела-Уоллиса для проверки гипотезы о наличии сдвига в параметрах положения сравниваемых выборок имеет вид

$H=\sum_{i=1}^k \left( 1-\frac{n_i}{N} \right) \left\{ \frac{\bar{R}_i-\frac{N+1}{2}}{\sqrt{\frac{(N-n_i)(N+1)}{12n_i}}} \right\} ^{\frac{1}{2}}=\frac{12}{N(N+1)}\sum_{i=1}^k n_i \left( \bar{R}_i-\frac{N+1}{2} \right) ^2 = \frac{12}{N(N+1)} \sum_{i=1}^k \frac{R_i^2}{n_i}-3(N+1),$

где $R_i=\sum_{j=1}^{n_i} R_i^j;\: \bar{R}_i=\frac{R_i}{n_i}$ .

При наличии связанных рангов (т.е. когда совпадают значения величин из разных выборок и им присваиваются одинаковые средние ранги) необходимо использовать модифицированную статистику $H*=H\left\{1-\left(\sum_{j=1}^q \frac{T_j}{N^3-N} \right) \right\} ^{-1},$ где $T_j=t_j^3-t_j;\; t_j$ — размер j-й группы одинаковых элементов; q — количество групп одинаковых элементов.

Гипотеза сдвига отклоняется на уровне значимости $\alpha$ , если $H \ge H_{\alpha}$ , где $H_{\alpha}$ — критическое значение, при $k \le 5$ и $n_i \le 8$ вычисляемое по таблицам. При больших значениях применимы различные аппроксимации.

При $n_i \ge 15$ справедлива аппроксимация распределения статистики $H$ $\chi_{k-1}^2$ -распределением с k-1 степенями свободы, т.е. нулевая гипотеза отклоняется, если $H \ge \chi_{k-1,\alpha}^2$ .

Аппроксимация Краскела-Уоллиса

Пусть

$M=\frac{N^3-\sum_{i=1}^k n_i^3}{N(N+1)};\; \nu_1=(k-1)\frac{(k-1)(M-k+1)-V}{\frac{1}{2}MV}; \nu_2==\frac{M-k+1}{k-1}\nu_1;\; V=2(k-1)-\frac{2\left\{3k^2-6k+N(2k^2-6k+1)\right\}}{5N(N+1)}-\frac{6}{5} \sum_{i=1}^k \frac{1}{n_i}.$

Тогда статистика

$F=\frac{H(M-k+1)}{(k-1)(M-H)}$

будет иметь при отсутствии сдвига распределение Фишера с $\nu_1$ и $\nu_2$ степенями свободы. Таким образом, нулевая гипотеза отклоняется с достоверностью $\alpha$ , если $F>F_{\alpha}(\nu_1,\nu_2)$ .

Аппроксимация Имана-Давенпорта

В соответстви с ней нулевая гипотеза сдвига отклоняется с достоверностью $\alpha$ , если $J \ge J_{\alpha}$ , где

$M=\frac{H}{2}\left(1+\frac{N-k}{N-1-H}\right);\; J_{\alpha}=\left\{(k-1)F_{\alpha}(k-1;N-l)+\chi_{\alpha}^2(k-1)\right},$

$\chi_{\alpha}^2(k-1)$ — критическое значение статистики хи-квадрат.

Это более точная аппроксимация, чем аппроксимация Краскела-Уоллиса.

Критические значения критерия Краскела-Уоллиса при k<=5, n<=8

Критические значения критерия Краскела-Уоллиса при k<=6, n<=8

См. также

Литература

Kruskal W. H. and Wallis W. A. Use of ranks in one-criterion variance analysis. // Journal of the American Statistical Association. — 1952, 47 №260. — Pp. 583–621.
Ликеш И., Ляга Й. Основные таблицы математической статистики. — М.: Финансы и статистика, 1985.
Кобзарь А. И. Прикладная математическая статистика. — М.: Физматлит, 2006. — 466-468 с.

Ссылки

Источник — «http://machinelearning.ru/wiki/index.php?title=%D0%9A%D1%80%D0%B8%D1%82%D0%B5%D1%80%D0%B8%D0%B9_%D0%9A%D1%80%D0%B0%D1%81%D0%BA%D0%B5%D0%BB%D0%B0-%D0%A3%D0%BE%D0%BB%D0%BB%D0%B8%D1%81%D0%B0»

Категории: Прикладная статистика | Статистические тесты | Дисперсионный анализ

@@ Строка 1: / Строка 1: @@
-'''Критерий Краскела-Уоллиса''' предназначена для проверки равенства средних нескольких выборок.
+'''Критерий Краскела-Уоллиса''' предназначен для проверки равенства средних нескольких выборок. Данный критерий является многовыборочным обобщением  [[Критерий Уилкоксона-Манна-Уитни|критерия Уилкоксона-Манна-Уитни]]. Критерий Краскела-Уоллиса является ранговым, поэтому он инвариантен по отношению к любому монотонному преобразованию шкалы измерения. Известен так же под названиями: критерий Крускала-Уоллиса, <i>H</i>-критерий Краскела-Уоллиса, Kruskal-Wallis one-way analysis of variance, Kruskal-Wallis test.
-Данный критерий является многомерным обобщением  [[Критерий Уилкоксона-Манна-Уитни|критерия Уилкоксона-Манна-Уитни]].
-Критерий Краскела-Уоллиса является ранговым, поэтому он инвариантен по отношению к любому монотонному преобразованию шкалы измерения.
-Известен так же под названиями: критерий Крускала-Уоллиса,<i>H</i>-критерий Краскела-Уоллиса, Kruskal-Wallis one-way analysis of variance, Kruskal-Wallis test.
 == Примеры задач ==
@@ Строка 8: / Строка 5: @@
 '''Пример 1.'''
 Проходит чемпионат мира по футболу.
-Первая выборка —- опрос болельщиков с вопросом "Каковы шансы на победу сборной России?" до начала чемпионата.
+Первая выборка — опрос болельщиков с вопросом "Каковы шансы на победу сборной России?" до начала чемпионата.
-Вторая выборка —- после первой игры, третья —- после второго матча и т.д.
+Вторая выборка — после первой игры, третья — после второго матча и т.д.
-Значения в выборках — шансы России на победу по десятибальной шкале (1 —- никаких перспектив, 10 —- отвезти в Россию кубок —- дело времени).
+Значения в выборках — шансы России на победу по десятибальной шкале (1 — никаких перспектив, 10 — отвезти в Россию кубок — дело времени).
 Требуется проверить, зависят ли результаты опросов от хода чемпионата.
+'''Пример 2.'''
+Выборка состоит из пациентов, у которых был диагностирован неизлечимый рак какого-либо органа. Всем им в качестве поддерживающей терапии был назначен к приёму витамин C (считалось, что он может способствовать выздоровлению раковых больных). Приведены данные об остаточной продолжительности жизни пациентов в днях. То есть выборка состоит из пар вида (пораженный орган, число дней), разделяясь на несколько числовых подвыборок, каждая из которых соответствует своему пораженному органу.
+Требуется проверить, отличается ли остаточная продолжительность жизни в зависимости от того, какой орган поражён раковой опухолью.
 == Описание критерия ==
-Заданы <i>k</i> выборок: <tex>x_1^{n_1}=\left\{x_{11},\dots,x_{1n_1}\right\}, \dots, x_k^{n_k}=\left\{x_{k1},\dots,x_{kn_k}\right\}</tex>.
+Заданы <i>k</i> выборок: <tex>X_1=\left\{x_1^1,\dots,x_1^{n_1}\right\}, \dots, X_k=\left\{x_k^1,\dots,x_k^{n_k}\right\}</tex>.
-Объединённая выборка: <tex>x=x_1^{n_1}\cup x_2^{n_2}\cup \dots \cup x_k^{n_k}</tex>.
+Объединённая выборка: <tex>X=X_1\cup X_2\cup \dots \cup X_k</tex>.
 ''Дополнительные предположения:''
-* обе выборки [[Простая выборка|простые]], объединённая выборка [[Независимая выборка|независима]];
+* все <i>k</i> выборок [[Простая выборка|простые]], объединённая выборка [[Независимая выборка|независима]];
 * выборки взяты из неизвестных непрерывных распределений  <tex>F_1(x),\dots,F_k(x)</tex>.
 Проверяется [[нулевая гипотеза]] <tex>H_0:\; F_1(x)=\dots=F_k(x)</tex> при альтернативе <tex>H_1:\; F_1(x)=F_2(x-\Delta_1)=\dots=F_k(x-\Delta_{k-1})</tex>.
-Упорядочим все <tex>N=\sum_{i=1}^k n_i</tex> элементов выборок по возрастанию и обозначим <tex>R_{ij}</tex> ранг <i>j</i>-го элемента <i>i</i>-й выборки в полученном [[вариационный ряд|вариационном ряду]].
+Упорядочим все <tex>N=\sum_{i=1}^k n_i</tex> элементов выборок по возрастанию и обозначим <tex>R_i^j</tex> ранг <i>j</i>-го элемента <i>i</i>-й выборки в полученном [[вариационный ряд|вариационном ряду]].
-Статистика критерия Краскела-Уоллиса для проверки гипотезы о наличии сдвига в параметрах положения двух сравниваемых выборок имеет вид <br />
+Статистика критерия Краскела-Уоллиса для проверки гипотезы о наличии сдвига в параметрах положения сравниваемых выборок имеет вид <br />
-:: <tex>H=\sum_{i=1}^k \left( 1-\frac{n_i}{N} \right) \left\{ \frac{\bar{R}_i-\frac{N+1}{2}}{\sqrt{\frac{(N-n_i)(N+1)}{12n_i}}} \right\} ^{\frac{1}{2}}=\frac{12}{N(N+1)}\sum_{i=1}^k \left( \bar{R}_i-\frac{N+1}{2} \right) ^2 = \frac{12}{N(N+1)} \sum_{i=1}^k \frac{R_i^2}{n_i}-3(N+1),</tex> <br />
+:: <tex>H=\sum_{i=1}^k \left( 1-\frac{n_i}{N} \right) \left\{ \frac{\bar{R}_i-\frac{N+1}{2}}{\sqrt{\frac{(N-n_i)(N+1)}{12n_i}}} \right\} ^{\frac{1}{2}}=\frac{12}{N(N+1)}\sum_{i=1}^k n_i \left( \bar{R}_i-\frac{N+1}{2} \right) ^2 = \frac{12}{N(N+1)} \sum_{i=1}^k \frac{R_i^2}{n_i}-3(N+1),</tex> <br />
-где <tex>R_i=\sum_{j=1}^k R_{ij};\: \bar{R}_i=\frac{1}{n_i}R_i</tex>.
+где <tex>R_i=\sum_{j=1}^{n_i} R_i^j;\: \bar{R}_i=\frac{R_i}{n_i}</tex>.
+При наличии связанных рангов (т.е. когда совпадают значения величин из разных выборок и им присваиваются одинаковые средние ранги) необходимо использовать модифицированную статистику <tex>H*=H\left\{1-\left(\sum_{j=1}^q \frac{T_j}{N^3-N} \right) \right\} ^{-1},</tex> где <tex>T_j=t_j^3-t_j;\; t_j</tex> — размер <i>j</i>-й группы одинаковых элементов; <i>q</i> — количество групп одинаковых элементов.
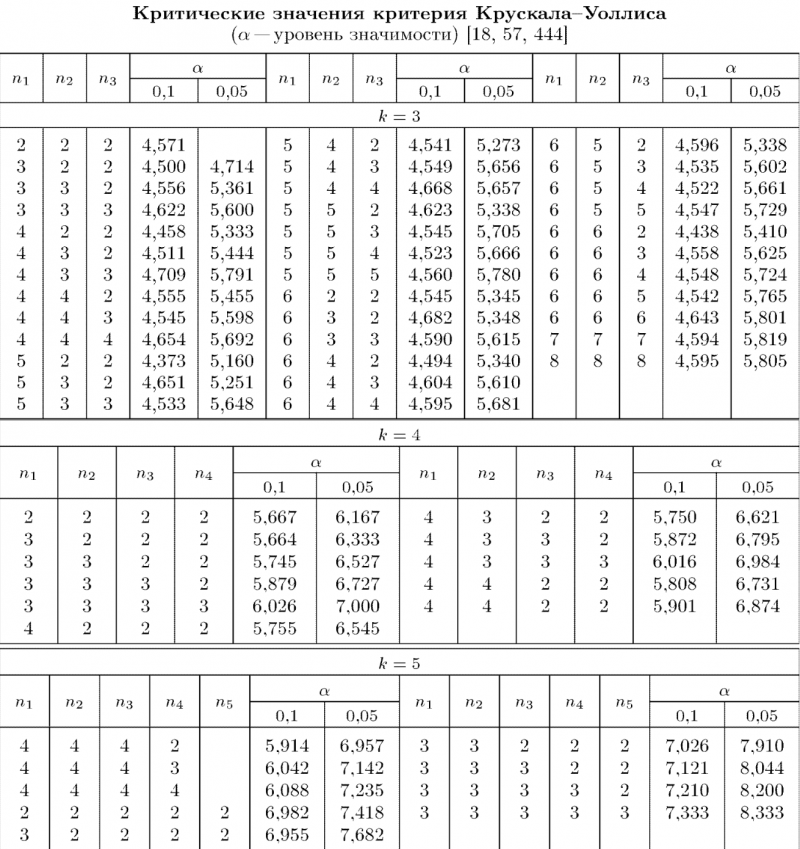
 Гипотеза сдвига отклоняется на уровне значимости <tex>\alpha</tex>, если <tex>H \ge H_{\alpha}</tex>, где <tex>H_{\alpha}</tex> — критическое значение, при <tex>k \le 5</tex> и <tex>n_i \le 8</tex> вычисляемое по таблицам.
-При бо{{подст:ударение}}льших значениях применимы различные аппроксимации.
+При больших значениях применимы различные аппроксимации.
+При <tex>n_i \ge 15</tex> справедлива аппроксимация распределения статистики <tex>H</tex> <tex>\chi_{k-1}^2</tex>-распределением с <i>k-1</i> степенями свободы, т.е. нулевая гипотеза отклоняется, если <tex>H \ge \chi_{k-1,\alpha}^2</tex>.
 === Аппроксимация Краскела-Уоллиса ===
@@ Строка 40: / Строка 46: @@
 Тогда статистика <br />
 <div align="center"><tex>F=\frac{H(M-k+1)}{(k-1)(M-H)}</tex></div> <br />
-будет иметь при отсутствии сдвига <i>F</i>-распределение с <tex>\nu_1</tex> и <tex>\nu_2</tex> степенями свободы.
+будет иметь при отсутствии сдвига распределение Фишера с <tex>\nu_1</tex> и <tex>\nu_2</tex> степенями свободы.
 Таким образом, нулевая гипотеза отклоняется с достоверностью <tex>\alpha</tex>, если <tex>F>F_{\alpha}(\nu_1,\nu_2)</tex>.
@@ Строка 47: / Строка 53: @@
 В соответстви с ней нулевая гипотеза сдвига отклоняется с достоверностью <tex>\alpha</tex>, если <tex>J \ge J_{\alpha}</tex>, где <br />
 ::<tex>M=\frac{H}{2}\left(1+\frac{N-k}{N-1-H}\right);\; J_{\alpha}=\left\{(k-1)F_{\alpha}(k-1;N-l)+\chi_{\alpha}^2(k-1)\right},</tex> <br />
-<tex>F_{\alpha}(f_1;f_2)</tex> и <tex>\chi_{\alpha}^2(a)</tex> — соответственно критические значения статистик Фишера и хи-квадрат с соответствующими степенями свободы.
+<tex>\chi_{\alpha}^2(k-1)</tex> — критическое значение статистики хи-квадрат.
 Это более точная аппроксимация, чем аппроксимация Краскела-Уоллиса.
-При наличии связанных рангов (т.е. когда совпадают значения величин из разных выборок и им присваиваются одинаковые средние ранги) необходимо использовать модифицированную статистику <tex>H*=H\left\{1-\left(\sum_{j=1}^q \frac{T_j}{N^3-N} \right) \right\} ^{-1},</tex> где <tex>T_j=t_j^3-t_j;\; t_j</tex> — размер <i>j</i>-й группы одинаковых элементов; <i>q</i> — количество групп одинаковых элементов.
-При <tex>n_i \ge 20</tex> справедлива аппроксимация распределения статистики <tex>H;\; \chi^2</tex>-распределением с <i>f=k-1</i> степенями свободы, т.е. нулевая гипотеза отклоняется, если <tex>H \ge \chi_{\alpha}^2(k-1)</tex>.
+== Критические значения критерия Краскела-Уоллиса при k<=5, n<=8 ==
+[[Изображение:Critical_values_for_Kruskal-Wallis_test.png|left|800px]]
+<br clear="both" />
+== Критические значения критерия Краскела-Уоллиса при k<=6, n<=8 ==
+[[Изображение:Critical_values_for_Kruskal-Wallis_test_k6.png|left|800px]]
+<br clear="both" />
 == См. также ==
-*[[Проверка статистических гипотез]]
+* [[Проверка статистических гипотез]]
-*[[Критерий Уилкоксона-Манна-Уитни]]
+* [[Критерий Уилкоксона-Манна-Уитни]]
-*[[Критерий знаков]]
+* [[Критерий знаков]]
+* [[Квантили распределения хи-квадрат]] [http://ru.wikipedia.org/wiki/%D0%9A%D0%B2%D0%B0%D0%BD%D1%82%D0%B8%D0%BB%D0%B8_%D1%80%D0%B0%D1%81%D0%BF%D1%80%D0%B5%D0%B4%D0%B5%D0%BB%D0%B5%D0%BD%D0%B8%D1%8F_%D1%85%D0%B8-%D0%BA%D0%B2%D0%B0%D0%B4%D1%80%D0%B0%D1%82 (ru_wiki)]
 == Литература ==
@@ Строка 67: / Строка 81: @@
 == Ссылки ==
-*[http://en.wikipedia.org/wiki/Kruskal-Wallis_one-way_analysis_of_variance Wikipedia: Kruskal-Wallis one-way analysis of variance]
+* [http://en.wikipedia.org/wiki/Kruskal-Wallis_one-way_analysis_of_variance Wikipedia: Kruskal-Wallis one-way analysis of variance]
-*[http://www.ed.sc.edu/seaman/edrm712/materials/KW%20AERA%202006.pdf Expanded Tables of Critical Values for the Kruskal-Wallis H Statistic]
+* [http://ami.nstu.ru/~headrd/seminar/publik_html/Homogeneity_averages.pdf О параметрических и непараметрических критериях проверки гипотез об однородности средних и их мощности на сайте Новосибирского государственного технического университета]
 [[Категория: Прикладная статистика]]
+[[Категория: Статистические тесты]]
+[[Категория:Дисперсионный анализ]]