Метод главных компонент
Материал из MachineLearning.
(→Литература) |
(→Поиск ортогональных проекций с наибольшим рассеянием) |
||
| (66 промежуточных версий не показаны.) | |||
| Строка 1: | Строка 1: | ||
| - | '''Метод | + | '''Метод Главных Компонент''' (англ. Principal Components Analysis, PCA) — один из основных способов уменьшить [[размерность]] данных, потеряв наименьшее количество [[информация|информации]]. Изобретен К. Пирсоном (англ.[http://en.wikipedia.org/wiki/Karl_Pearson Karl Pearson]) в 1901 г. Применяется во многих областях, таких как [[распознавание образов]], [[компьютерное зрение]], [[сжатие данных]] и т. п. Вычисление главных компонент сводится к вычислению собственных векторов и собственных значений [[Ковариационная матрица| ковариационной матрицы]] исходных данных или к [[Сингулярное разложение|сингулярному разложению]] матрицы данных. Иногда метод главных компонент называют ''преобразованием Кархунена-Лоэва'' (англ. Karhunen-Loeve)<ref>В русскоязычной научной литературе распространено также написание ''преобразование Карунена-Лоэва'', соответствующее английскому прочтению финской фамилии</ref> или преобразованием Хотеллинга (англ. Hotelling transform). Другие способы уменьшения размерности данных — это [[метод независимых компонент]], многомерное шкалирование, а также многочисленные нелинейные обобщения: метод главных кривых и многообразий, [[Поиск наилучшей проекции|поиск наилучшей проекции]] (англ. Projection Pursuit), [[Искусственная нейронная сеть|нейросетевые]] методы «[[Нейросетевое сжатие данных|узкого горла]]», [[Нейронная сеть Кохонена|самоорганизующиеся карты Кохонена]] и др. |
| - | + | ||
| - | + | ||
| - | + | ||
| - | == | + | == Формальная постановка задачи == |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | Задача анализа главных компонент, имеет, как минимум, четыре базовых версии: | |
| - | + | * аппроксимировать данные линейными многообразиями меньшей размерности; | |
| - | + | * найти подпространства меньшей размерности, в ортогональной проекции на которые разброс данных (т.е. среднеквадратичное уклонение от среднего значения) максимален; | |
| - | + | * найти подпространства меньшей размерности, в ортогональной проекции на которые среднеквадратичное расстояние между точками максимально; | |
| - | + | * для данной многомерной случайной величины построить такое ортогональное преобразование координат, что в результате корреляции между отдельными координатами обратятся в ноль. | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | Первые три версии оперируют конечными множествами данных. Они эквивалентны и не используют никакой гипотезы о статистическом порождении данных. Четвёртая версия оперирует случайными величинами. Конечные множества появляются здесь как выборки из данного распределения, а решение трёх первых задач — как приближение к «истинному» преобразованию Кархунена-Лоэва. При этом возникает дополнительный и не вполне тривиальный вопрос о точности этого приближения. | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | == | + | === Аппроксимация данных линейными многообразиями === |
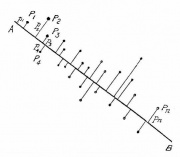
| - | + | [[Изображение:PearsonFig.jpg|thumb|Иллюстрация к знаменитой работе К. Пирсона (1901): даны точки <tex> P_i</tex> на плоскости, <tex> p_i</tex> — расстояние от <tex> P_i</tex> до прямой <tex> AB</tex>. Ищется прямая <tex> AB</tex>, минимизирующая сумму <tex>\sum_i p_i^2</tex> ]] | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | Метод главных компонент начинался с задачи наилучшей аппроксимации конечного множества точек прямыми и плоскостями (К. Пирсон, 1901). Дано конечное множество векторов <tex>x_1,x_2,...x_m \in\mathbb{R}^n </tex>. Для каждого <tex> k = 0,1,..., n-1 </tex> среди всех <tex>k</tex>-мерных линейных многообразий в <tex>\mathbb{R}^n </tex> найти такое <tex>L_k \subset \mathbb{R}^n </tex>, что сумма квадратов уклонений <tex> x_i</tex> от <tex> L_k</tex> минимальна: | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | == | + | : <tex>\sum_{i=1}^m \operatorname{dist}^2(x_i, L_k) \to \min</tex>, |
| - | * [[ | + | |
| - | * [[ | + | где <tex>\operatorname{dist}(x_i, L_k) </tex> — евклидово расстояние от точки до линейного многообразия. Всякое <tex>k </tex>-мерное линейное многообразие в <tex>\mathbb{R}^n </tex> может быть задано как множество линейных комбинаций <tex>L_k = \{ a_0 +\beta_1 a_1 +...+ \beta_k a_k | \beta_i \in \mathbb{R} \} </tex>, где параметры <tex> \beta_i </tex> пробегают вещественную прямую <tex>\mathbb{R}</tex>, <tex>a_0 \in \mathbb{R}^n</tex> а <tex>\left\{a_1,..., a_k \right\} \subset \mathbb{R}^n</tex> — ортонормированный набор векторов |
| - | * [[ | + | : <tex>\operatorname{dist}^2(x_i, L_k) = \| x_i - a_0 - \sum_{j=1}^k a_j (a_j, x_i - a_0) \| ^2</tex>, |
| + | где <tex>\|^\ \cdot \ \|^\ </tex> евклидова норма, <tex> \left(a_j, x_i\right) </tex> — евклидово скалярное произведение, или в координатной форме: | ||
| + | : <tex> \operatorname{dist}^2(x_i, L_k) = \sum_{l=1}^n \left(x_{il} - a_{0l}- \sum_{j=1}^k a_{jl} \sum_{q=1}^n a_{jq}(x_{iq} - a_{0q}) \right)^2 </tex>. | ||
| + | |||
| + | Решение задачи аппроксимации для <tex> k = 0,1,..., n-1 </tex> даётся набором вложенных линейных многообразий <tex>L_0 \subset L_1 \subset ... L_{n-1} </tex>, <tex>L_k = \{ a_0 +\beta_1 a_1 +...+ \beta_k a_k | \beta_i \in \mathbb{R} \} </tex>. Эти линейные многообразия определяются ортонормированным набором векторов <tex>\left\{a_1,..., a_{n-1} \right\} </tex> (векторами главных компонент) и вектором <tex> a_0 </tex>. | ||
| + | Вектор <tex> a_0 </tex> ищется, как решение задачи минимизации для <tex> L_0 </tex>: | ||
| + | |||
| + | : <tex> a_0 = \underset{a_0\in\mathbb{R}^n}{\operatorname{argmin}} \left(\sum_{i=1}^m \operatorname{dist}^2(x_i, L_0)\right), </tex> | ||
| + | |||
| + | то есть | ||
| + | |||
| + | : <tex>a_0 = \underset{a_0\in\mathbb{R}^n}{\operatorname{argmin}} \left (\sum_{i=1}^m \| x_i - a_0\| ^2\right) </tex>. | ||
| + | |||
| + | Это — [[выборочное среднее]]: <tex>a_0 = \frac{1}{m} \sum_{i=1}^m x_i = \overline{X}.</tex> | ||
| + | [[Фреше, Морис Рене|Фреше]] в [[1948 год]]у обратил внимание, что вариационное определение среднего (как точки, минимизирующей сумму квадратов расстояний до точек данных) очень удобно для построения статистики в произвольном [[Метрическое пространство|метрическом пространстве]], и построил обобщение классической статистики для общих пространств (обобщённый [[метод наименьших квадратов]]). | ||
| + | |||
| + | Векторы главных компонент могут быть найдены как решения однотипных задач [[Оптимизация (математика)|оптимизации]]: | ||
| + | : 1) централизуем данные (вычитаем среднее): <tex>x_i:= x_i - \overline{X_i}</tex>. Теперь <tex>\sum_{i=1}^m x_i =0 </tex>; | ||
| + | : 2) находим первую главную компоненту как решение задачи; | ||
| + | :: <tex>a_1 = \underset{\| a_1 \| =1}{\operatorname{argmin}} \left( \sum_{i=1}^m \| x_i - a_1 (a_1,x_i)\| ^2\right)</tex>. | ||
| + | :: Если решение не единственно, то выбираем одно из них. | ||
| + | : 3) Вычитаем из данных проекцию на первую главную компоненту: | ||
| + | :: <tex>x_i:= x_i - a_1 \left(a_1,x_i\right) </tex>; | ||
| + | : 4) находим вторую главную компоненту как решение задачи | ||
| + | :: <tex>a_2 = \underset{\| a_2 \| =1}{\operatorname{argmin}} \left( \sum_{i=1}^m \| x_i - a_2 (a_2,x_i)\| ^2\right) </tex>. | ||
| + | :: Если решение не единственно, то выбираем одно из них. | ||
| + | :: … | ||
| + | : 2k-1) Вычитаем проекцию на <tex>(k-1)</tex>-ю главную компоненту (напомним, что проекции на предшествующие <tex>(k-2)</tex> главные компоненты уже вычтены): | ||
| + | :: <tex>x_i:= x_i - a_{k-1} \left(a_{k-1},x_i\right) </tex>; | ||
| + | : 2k) находим k-ю главную компоненту как решение задачи: | ||
| + | :: <tex>a_k = \underset{\| a_k \| =1}{\operatorname{argmin}} \left( \sum_{i=1}^m \| x_i - a_k (a_k,x_i)\| ^2\right) </tex>. | ||
| + | :: Если решение не единственно, то выбираем одно из них. | ||
| + | :: … | ||
| + | На каждом подготовительном шаге <tex> (2k-1)</tex> вычитаем проекцию на предшествующую главную компоненту. Найденные векторы <tex>\left\{a_1,..., a_{ n -1} \right\}</tex> ортонормированы просто в результате решения описанной задачи оптимизации, однако чтобы не дать ошибкам вычисления нарушить взаимную ортогональность векторов главных компонент, можно включать <tex>a_k \bot \{a_1,..., a_{k -1} \} </tex> в условия задачи оптимизации. | ||
| + | |||
| + | Неединственность в определении <tex> a_k</tex> помимо тривиального произвола в выборе знака (<tex> a_k</tex> и <tex> -a_k</tex> решают ту же задачу) может быть более существенной и происходить, например, из условий симметрии данных. | ||
| + | |||
| + | === Поиск ортогональных проекций с наибольшим рассеянием === | ||
| + | |||
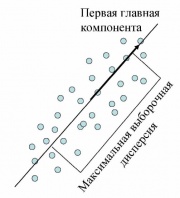
| + | [[Изображение:FirstPrincipalComponent.jpg|thumb|Первая главная компонента максимизирует выборочную дисперсию проекции данных]] | ||
| + | |||
| + | |||
| + | Пусть нам дан центрированный набор векторов данных <tex>x_i\in\mathbb{R}^n \; (i=1,...,m)</tex> (среднее арифметическое значение <tex> x_i </tex> равно нулю). Задача — найти такое ортогональное преобразование в новую систему координат, для которого были бы верны следующие условия: | ||
| + | * [[Выборочная дисперсия]] данных вдоль первой координаты максимальна (эту координату называют первой ''главной компонентой''); | ||
| + | * Выборочная дисперсия данных вдоль второй координаты максимальна при условии ортогональности первой координате (вторая главная компонента); | ||
| + | * … | ||
| + | * Выборочная дисперсия данных вдоль значений <tex>k</tex>-ой координаты максимальна при условии ортогональности первым <tex>k-1</tex> координатам; | ||
| + | * … | ||
| + | |||
| + | Выборочная дисперсия данных вдоль направления, заданного нормированным вектором <tex> a_k</tex>, это | ||
| + | : <tex>S^2_m \left[ (X, a_k) \right ] = \frac{1}{m} \sum\limits_{i=1}^m \left(\sum\limits_{j=1}^n x_{ij}a_{kj} \right)^2</tex> | ||
| + | (поскольку данные центрированы, выборочная дисперсия здесь совпадает со средним квадратом уклонения от нуля). | ||
| + | |||
| + | Формально, если <tex>A=\left \{a_1,...,a_n \right \}^T\in\mathbb{R}^{n \times n}</tex>, <tex>a_k\in\mathbb{R}^n</tex> — искомое преобразование, то для векторов <tex>a_k</tex> должны выполняться следующие условия: | ||
| + | * <tex>a_1 = \underset{\| a_1 \| =1}{\operatorname{argmax}}\,S^2_m \left [(X, a_1) \right ];</tex> | ||
| + | : Если решение не единственно, то выбираем одно из них. | ||
| + | * Вычитаем из данных проекцию на первую главную компоненту: | ||
| + | : <tex>x_i:= x_i-a_1 \left(a_1,x_i\right) </tex>; в результате <tex>x_i \bot a_1</tex>; | ||
| + | * находим вторую главную компоненту как решение задачи | ||
| + | : <tex>a_2 = \underset{\| a_2 \| =1}{\operatorname{argmax}}\,S^2_m \left [ (X, a_2) \right ];</tex> | ||
| + | : Если решение не единственно, то выбираем одно из них. | ||
| + | * … | ||
| + | * Вычитаем проекцию на <tex>(k-1)</tex>-ю главную компоненту (напомним, что проекции на предшествующие <tex>k-2</tex> главные компоненты уже вычтены): | ||
| + | : <tex>x_i:= x_i-a_{k-1} \left(a_{k-1},x_i\right) </tex>; в результате <tex>x_i \bot a_l, (l = 1,\dots k-1)</tex>; | ||
| + | * находим <tex>k</tex>-ю главную компоненту как решение задачи | ||
| + | : <tex>a_n = \underset{\| a_k\| = 1}{\operatorname{argmax}}\,S^2_m \left [ (X, a_k) \right ];</tex> | ||
| + | : Если решение не единственно, то выбираем одно из них. | ||
| + | * ... | ||
| + | |||
| + | Фактически, как и для задачи аппроксимации, на каждом шаге решается задача о первой главной компоненте для данных, из которых вычтены проекции на все ранее найденные главные компоненты. При большом числе итерации (большая размерность, много главных компонент) отклонения от ортогональности накапливаются и может потребоваться специальная коррекция [[алгоритм]]а или другой алгоритм поиска собственных векторов ковариационной матрицы. | ||
| + | |||
| + | Решение задачи о наилучшей аппроксимации даёт то же множество решений <tex>\left\{a_i\right\}</tex>, что и поиск ортогональных проекций с наибольшим рассеянием, по очень простой причине: <tex>\| x_i-a_k (a_k, x_i)\|^2 \stackrel{\|a_k\|=1}{=} \| x_i\|^2-(a_k, x_i)^2, </tex> и первое слагаемое не зависит от <tex> a_k</tex>. Только одно дополнение к задаче об аппроксимации: появляется последняя главная компонента <tex> a_n.</tex> | ||
| + | |||
| + | === Поиск ортогональных проекций с наибольшим среднеквадратичным расстоянием между точками === | ||
| + | |||
| + | Ещё одна эквивалентная формулировка следует из очевидного тождества, верного для любых <tex>m</tex> векторов <tex> x_i</tex>: | ||
| + | : <tex>\frac{1}{m(m-1)}\sum_{i,j=1}^m (x_i-x_j)^2 =\frac{2m^2}{m(m-1)}\left[\frac{1}{m}\sum_{i=1}^m x_i^2 - \left(\frac{1}{m}\sum_{i}^m x_i \right)^2\right].</tex> | ||
| + | В левой части этого тождества стоит среднеквадратичное расстояние между точками, а в квадратных скобках справа — выборочная дисперсия. Таким образом, в методе главных компонент ищутся подпространства, в проекции на которые среднеквадратичное расстояние между точками максимально (или, что то же самое, его искажение в результате проекции минимально)<ref>''Зиновьев А. Ю.'', [http://pca.narod.ru/ZINANN.htm Визуализация многомерных данных], Красноярск, Изд. КГТУ, 2000.</ref>. Такая переформулировка позволяет строить обобщения с взвешиванием различных парных расстояний (а не только точек). | ||
| + | |||
| + | === Аннулирование корреляций между координатами === | ||
| + | |||
| + | Для заданной <tex> n</tex>-мерной случайной величины <tex> X</tex> найти такой ортонормированный базис, <tex>\left\{a_1,..., a_n \right\}</tex>, в котором коэффициент ковариации между различными координатами равен нулю. После преобразования к этому базису | ||
| + | |||
| + | : <tex>\operatorname{cov}(X_i,X_j)=0</tex> для <tex>i \neq j </tex>. | ||
| + | |||
| + | Здесь <tex> \operatorname{cov}(X_i,X_j)= \operatorname{E}[(X_i-\overline{X_i})(X_j-\overline{X_j})] </tex> — коэффициент ковариации. | ||
| + | |||
| + | == Диагонализация ковариационной матрицы == | ||
| + | |||
| + | Все задачи о главных компонентах приводят к задаче диагонализации ковариационной матрицы или выборочной ковариационной матрицы. Эмпирическая или выборочная ковариационная матрица, это | ||
| + | : <tex>C = [c_{ij}],\ c_{ij} = \frac{1}{m-1} \sum_{l=1}^m (x_{li}-\overline{X_{i}})(x_{lj}-\overline{X_{j}}).</tex> | ||
| + | [[Ковариационная матрица]] многомерной случайной величины <tex> X</tex>, это | ||
| + | : <tex>\Sigma = [\sigma_{ij}],\ \sigma_{ij} = \operatorname{cov}(X_i,X_j)=E[(X_i-\overline{X_i})(X_j-\overline{X_j})].</tex> | ||
| + | Векторы главных компонент для задач о наилучшей аппроксимации и о поиске ортогональных проекций с наибольшим рассеянием — это ортонормированный набор <tex> \left\{a_1,..., a_n \right\}</tex> собственных векторов эмпирической ковариационной матрицы <tex>C</tex>, расположенных в порядке убывания собственных значений <tex>\lambda: \lambda_1 \ge \lambda_2 \ge ... \ge \lambda_n \ge 0. </tex> Эти векторы служат оценкой для собственных векторов ковариационной матрицы <tex>\operatorname{cov}(X_i,X_j) </tex>. В базисе из собственных векторов ковариационной матрицы она, естественно, диагональна, и в этом базисе коэффициент ковариации между различными координатами равен нулю. | ||
| + | |||
| + | Если спектр ковариационной матрицы вырожден, то выбирают произвольный ортонормированный базис собственных векторов. Он существует всегда, а собственные числа ковариационной матрицы всегда вещественны и неотрицательны. | ||
| + | |||
| + | == [[Сингулярное разложение]] матрицы данных == | ||
| + | |||
| + | {{main|Простой итерационный алгоритм сингулярного разложения}} | ||
| + | |||
| + | Математическое содержание метода главных компонент — это ''спектральное разложение'' ковариационной матрицы <tex> C </tex>, то есть представление пространства данных в виде суммы взаимно ортогональных собственных подпространств <tex> C </tex>, а самой матрицы <tex> C </tex> — в виде линейной комбинации ортогональных проекторов на эти подпространства с коэффициентами <tex> \lambda_i </tex>. Если <tex>\operatorname{X}=\left\{x_1,..., x_m \right\}^T</tex> — матрица, составленная из векторов-строк центрированных данных, то <tex> C = \frac{1}{m-1}\operatorname{X}^T\operatorname{X}</tex> и задача о спектральном разложении ковариационной матрицы <tex> C </tex> превращается в задачу о ''сингулярном разложении'' (англ. [http://en.wikipedia.org/wiki/Singular_value_decomposition Singular value decomposition]) матрицы данных <tex>\operatorname{X}</tex>. | ||
| + | |||
| + | Хотя формально задачи сингулярного разложения матрицы данных и спектрального разложения ковариационной матрицы совпадают, [[алгоритм]]ы вычисления сингулярного разложения напрямую, без вычисления ковариационной матрицы и её спектра, более эффективны и устойчивы <ref>''Bau III, D., Trefethen, L. N.'', [http://books.google.com/books?id=bj-Lu6zjWbEC&pg=PA136&dq=isbn:9780898713619&sig=BmAatL8LDJZZRhfJIFVRHLQNJw0#PPP1,M1 Numerical linear algebra], Philadelphia: Society for Industrial and Applied Mathematics, 1997. (Lecture 31) ISBN 978-0-89871-361-9 </ref>. | ||
| + | |||
| + | Теория сингулярного разложения была создана Дж. Дж. Сильвестром (англ. [http://en.wikipedia.org/wiki/James_Joseph_Sylvester J. J. Sylvester]) в 1889 г. и изложена во всех подробных руководствах по теории матриц <ref>''Гантмахер Ф. Р.'', Теория матриц. — М.: Наука, 1966. — 576 стр.</ref>. | ||
| + | |||
| + | == Матрица преобразования к главным компонентам == | ||
| + | |||
| + | Матрица <tex>A</tex> преобразования данных к главным компонентам строится из векторов главных компонент: <tex>A=\left \{a_1,...,a_n \right \}^T</tex>. Здесь <tex> a_i</tex> — ортонормированные векторы-столбцы главных компонент, расположенные в порядке убывания собственных значений, верхний индекс <tex> T</tex> означает транспонирование. Матрица <tex>A</tex> является [[Ортогональная матрица|ортогональной]]: <tex>A A^T=1</tex>. | ||
| + | |||
| + | После преобразования большая часть вариации данных будет сосредоточена в первых координатах, что даёт возможность отбросить оставшиеся и рассмотреть пространство уменьшенной размерности. | ||
| + | |||
| + | == Остаточная дисперсия == | ||
| + | Пусть данные центрированы, <tex>\overline{ X}=0</tex>. При замене векторов данных <tex> x_i</tex> на их проекцию на первые <tex> k</tex> главных компонент <tex>x_i \mapsto \sum_{j=1}^k a_j (a_j, x_i) </tex> вносится средний квадрат ошибки в расчете на один вектор данных: | ||
| + | : <tex>\frac{1}{m} \sum_{i=1}^m \left\| x_i - \sum_{j=1}^k a_j (a_j, x_i) \right \| ^2=\sum_{l=k+1}^n \lambda_l, </tex> | ||
| + | где <tex>\lambda_1 \ge \lambda_2 \ge ... \ge \lambda_n \ge 0</tex> собственные значения эмпирической ковариационной матрицы <tex>C</tex>, расположенные в порядке убывания, с учетом кратности. | ||
| + | |||
| + | Эта величина называется ''остаточной дисперсией''. Величина | ||
| + | : <tex>\frac{1}{m} \sum_{i=1}^m \left\| \sum_{j=1}^k a_j (a_j, x_i) \right\| ^2=\frac{1}{m} \sum_{i=1}^m \sum_{j=1}^k (a_j, x_i)^2=\sum_{l=1}^k \lambda_l </tex> | ||
| + | называется ''объяснённой дисперсией''. Их сумма равна выборочной дисперсии. Соответствующий квадрат относительной ошибки — это отношение остаточной дисперсии к выборочной дисперсии (то есть ''доля необъяснённой дисперсии''): | ||
| + | : <tex>\delta^2_k=\frac{\lambda_{k+1}+\lambda_{k+2}+...+\lambda_{n}}{\lambda_{1}+\lambda_{2}+...+\lambda_{n}}.</tex> | ||
| + | |||
| + | По относительной ошибке <tex> \delta_k</tex> оценивается применимость метода главных компонент с проецированием на первые <tex> k</tex> компонент. | ||
| + | |||
| + | '''Замечание''': в большинстве вычислительных алгоритмов собственные числа <tex> \lambda_i</tex> с соответствуюшими собственными векторами — главными компонентами <tex> a_i</tex> вычисляются в порядке «от больших <tex> \lambda_i</tex> — к меньшим». Для вычисления <tex> \delta_k</tex> достаточно вычислить первые <tex> k</tex> собственных чисел и след эмпирической ковариационной матрицы <tex>C</tex>, <tex>\operatorname{tr} C</tex> (сумму диагональных элементов <tex>C</tex>, то есть дисперсий по осям). Тогда | ||
| + | : <tex>\delta^2_k=\frac{1}{\operatorname{tr} C}\left(\operatorname{tr} C -\sum_{i=1}^k \lambda_{i}\right).</tex> | ||
| + | |||
| + | == Оценка числа главных компонент по правилу сломанной трости == | ||
| + | |||
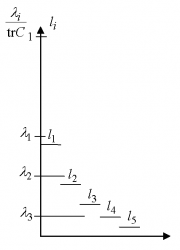
| + | [[Изображение:5DFig.png|thumb|Пример: оценка числа главных компонент по правилу сломанной трости в размерности 5.]] | ||
| + | Целевой подход к оценке числа главных компонент по необходимой доле объяснённой дисперсии формально применим всегда, однако неявно он предполагает, что нет разделения на "сигнал" и "шум", и любая заранее заданная точность имеет смысл. Поэтому часто более продуктивна иная эвристика, основывающаяся на гипотезе о наличии "сигнала" (сравнительно малая размерность, относительно большая амплитуда) и "шума" (большая размерность, относительно малая амплитуда). С этой точки зрения метод главных компонент работает как фильтр: сигнал содержится, в основном, в проекции на первые главные компоненты, а в остальных компонентах пропорция шума намного выше. | ||
| + | |||
| + | Вопрос, как оценить число необходимых главных компонент, если отношение "сигнал/шум" заранее неизвестно? Одним из наиболее популярных эвристических подходов является правило сломанной трости (англ. Broken stick model)<ref>''Cangelosi R. '', ''Goriely A.'', [http://www.biology-direct.com/content/2/1/2 Component retention in principal component analysis with application to cDNA microarray data], Biology Direct 2007, 2:2. [http://pca.narod.ru/ А также на сайте PCA].</ref>. Набор нормированных собственных чисел (<tex>\lambda_i / \tr C</tex>, <tex>i=1,...,n</tex>) сравнивается с распределением длин обломков трости единичной длины, сломанной в <tex>n-1</tex>-й случайно выбранной точке (точки разлома выбираются независимо и равнораспределены по длине трости). Пусть <tex>L_i</tex> (<tex>i=1,...,n</tex>) - длины полученных кусков трости, занумерованные в порядке убывания длины: <tex>L_1 \geq L_2 \geq \ldots \geq L_n</tex>. Нетрудно найти математическое ожидание <tex>L_i</tex>: | ||
| + | :<tex>l_i=\operatorname{E}(L_i)=\frac{1}{n}\sum_{j=i}^{n} \frac{1}{j}.</tex> | ||
| + | По правилу сломанной трости <tex>k</tex>-й собственный вектор (в порядке убывания собственных чисел <tex>\lambda_i</tex>) сохраняется в списке главных компонент, если | ||
| + | :<tex>\frac{\lambda_1}{\tr C}>l_1 \& \frac{\lambda_2}{\tr C}>l_2 \& \ldots \& \frac{\lambda_k}{\tr C}>l_k.</tex> | ||
| + | На Рис. приведён пример для 5-мерного случая: | ||
| + | :<tex>l_1</tex>=(1+1/2+1/3+1/4+1/5)/5; <tex>l_2</tex>=(1/2+1/3+1/4+1/5)/5; <tex>l_3</tex>=(1/3+1/4+1/5)/5; <tex>l_4</tex>=(1/4+1/5)/5; <tex>l_5</tex>=(1/5)/5. | ||
| + | Для примера выбрано | ||
| + | :<tex>\frac{\lambda_1}{\tr C}</tex>=0.5; <tex>\frac{\lambda_2}{\tr C}</tex>=0.3; <tex>\frac{\lambda_3}{\tr C}</tex>=0.1; <tex>\frac{\lambda_4}{\tr C}</tex>=0.06; <tex>\frac{\lambda_5}{\tr C}</tex>=0.04. | ||
| + | По правилу сломанной трости в этом примере следует оставлять 2 главных компоненты: | ||
| + | :<tex>\frac{\lambda_1}{\tr C}>l_1 \;; \; \frac{\lambda_2}{\tr C}>l_2 \;; \;\frac{\lambda_3}{\tr C}<l_3\;.</tex> | ||
| + | |||
| + | == Нормировка == | ||
| + | |||
| + | === Нормировка после приведения к главным компонентам === | ||
| + | |||
| + | ''После'' проецирования на первые <tex> k</tex> главных компонент с <tex>\lambda_1 \ge \lambda_2 \ge ... \ge \lambda_k > 0</tex> удобно произвести нормировку на единичную (выборочную) дисперсию по осям. Дисперсия вдоль <tex> i</tex>й главной компоненты равна | ||
| + | <tex>\lambda_i > 0 \; (1 \le i \le k</tex>), поэтому для нормировки надо разделить соответствующую координату на <tex> \sqrt{ \lambda_i}</tex>. Это преобразование не является ортогональным и не сохраняет скалярного произведения. Ковариационная матрица проекции данных после нормировки становится единичной, проекции на любые два ортогональных направления становятся независимыми величинами, а любой ортонормированный базис становится базисом главных компонент (напомним, что нормировка меняет отношение ортогональности векторов). Отображение из пространства исходных данных на первые <tex> k</tex> главных компонент вместе с нормировкой задается матрицей | ||
| + | |||
| + | : <tex>K=\left \{\frac{a_1}{\sqrt{ \lambda_1}},\frac{a_2}{\sqrt{ \lambda_2}},...,\frac{a_k}{\sqrt{ \lambda_k}} \right \}^T</tex>. | ||
| + | |||
| + | Именно это преобразование чаще всего называется преобразованием Кархунена-Лоэва. Здесь <tex> a_i</tex> — векторы-столбцы, а верхний индекс <tex> T</tex> означает транспонирование. | ||
| + | |||
| + | === Нормировка до вычисления главных компонент === | ||
| + | |||
| + | '''Предупреждение''': не следует путать нормировку, проводимую после преобразования к главным компонентам, с нормировкой и «обезразмериванием» при ''предобработке данных'', проводимой до вычисления главных компонент. Предварительная нормировка нужна для обоснованного выбора метрики, в которой будет вычисляться наилучшая аппроксимация денных, или будут искаться направления наибольшего разброса (что эквивалентно). Например, если данные представляют собой трёхмерные векторы из «метров, литров и килограмм», то при использовании стандартного евклидового расстояния разница в 1 метр по первой координате будет вносить тот же вклад, что разница в 1 литр по второй, или в 1 кг по третьей. Обычно системы единиц, в которых представлены исходные данные, недостаточно точно отображают наши представления о естественных масштабах по осям, и проводится «обезразмеривание»: каждая координата делится на некоторый масштаб, определяемый данными, целями их обработки и процессами измерения и сбора данных. | ||
| + | |||
| + | Есть три cущественно различных стандартных подхода к такой нормировке: на ''единичную дисперсию'' по осям (масштабы по осям равны средним квадратичным уклонениям — после этого преобразования ковариационная матрица совпадает с матрицей [[Коэффициент корреляции|коэффициентов корреляции]]), на ''равную точность измерения'' (масштаб по оси пропорционален точности измерения данной величины) и на ''равные требования'' в задаче (масштаб по оси определяется требуемой точностью прогноза данной величины или допустимым её искажением — уровнем толерантности). На выбор предобработки влияют содержательная постановка задачи, а также условия сбора данных (например, если коллекция данных принципиально не завершена и данные будут ещё поступать, то нерационально выбирать нормировку строго на единичную дисперсию, даже если это соответствует смыслу задачи, поскольку это предполагает перенормировку всех данных после получения новой порции; разумнее выбрать некоторый масштаб, грубо оценивающий стандартное отклонение, и далее его не менять). | ||
| + | |||
| + | Предварительная нормировка на единичную дисперсию по осям разрушается поворотом системы координат, если оси не являются главными компонентами, и нормировка при предобработке данных не заменяет нормировку после приведения к главным компонентам. | ||
| + | |||
| + | == Механическая аналогия и метод главных компонент для взвешенных данных == | ||
| + | |||
| + | Если сопоставить каждому вектору данных единичную массу, то эмпирическая ковариационная матрица | ||
| + | <tex> C</tex> совпадёт с [[Момент инерции#Тензор инерции и эллипсоид инерции|тензором инерции]] этой системы точечных масс (делённым на полную массу <tex> m</tex>), а задача о главных компонентых — с задачей приведения тензора инерции к главным осям. Можно использовать дополнительную свободу в выборе значений масс для учета важности точек данных или надежности их значений (важным данным или данным из более надежных источников приписываются бо́льшие массы). Если '''вектору данных <tex> x_l</tex> придаётся масса <tex> w_l</tex>,''' то вместо эмпирической ковариационной матрицы <tex> C</tex> получим | ||
| + | : <tex>C^w = [c^w_{ij}],\ c^w_{ij} = \frac{1}{\sum_{l} w_l} \sum_{l=1}^m w_l(x_{li}-\overline{X_{i}})(x_{lj}-\overline{X_{j}}).</tex> | ||
| + | Все дальнейшие операции по приведению к главным компонентам производятся так же, как и в основной версии метода: ищем ортонормированный собственный базис <tex> C^w</tex>, упорядочиваем его по убыванию собственных значений, оцениваем средневзвешенную ошибку аппроксимации данных первыми <tex> k</tex> компонентами (по суммам собственных чисел <tex> C^w</tex>), нормируем и т. п. | ||
| + | |||
| + | Более общий способ взвешивания даёт '''максимизация взвешенной суммы попарных расстояний'''<ref>''Koren Y., Carmel L.,'' Robust linear dimensionality reduction, IEEE Transactions on Visualisation and Computer Graphics, 10 (4) (2004), 459—470. [http://pca.narod.ru/ А также на сайте PCA]</ref> между проекциями. Для каждых двух точек данных, <tex>x_l , \ x_q</tex> вводится вес <tex>d_{lq}</tex>; <tex>d_{lq}=d_{ql}</tex> и <tex>d_{l}=\sum_{q=1}^m d_{lq}</tex>. Вместо эмпирической ковариационной матрицы <tex> C</tex> используется | ||
| + | : <tex>C^d = [c^d_{ij}],\ c^d_{ij} =\sum_{l=1}^m d_l (x_{li}-\overline{X_{i}})(x_{lj}-\overline{X_{j}}) -\sum_{l \neq q, \ l,q=1}^m d_{lq}(x_{li} - \overline{X_{i}})(x_{qj}- \overline{X_{j}}).</tex> | ||
| + | При <tex>d_{lq}>0</tex> симметричная матрица <tex>C^d</tex> положительно определена, поскольку положительна квадратичная форма: | ||
| + | :<tex>\sum_{ij} c^d_{ij}a_i a_j = \frac{1}{2}\sum_{lq}d_{lq}\left(\sum_ia_i(x_{li}-x_{qi})\right)^2.</tex> | ||
| + | Далее ищем ортонормированный собственный базис <tex> C^d</tex>, упорядочиваем его по убыванию собственных значений, оцениваем средневзвешенную ошибку аппроксимации данных первыми <tex> k</tex> компонентами и т. д. — в точности так же, как и в основном алгоритме. | ||
| + | |||
| + | Этот способ применяется ''при наличии классов'': для <tex>x_l , \ x_q</tex> из разных классов вес <tex>d_{lq}</tex> вес выбирается бо́льшим, чем для точек одного класса. В результате, в проекции на взвешенные главные компоненты различные классы «раздвигаются» на большее расстояние. | ||
| + | |||
| + | Другое применение — ''снижение влияния больших уклонений'' (оутлайеров, англ.[http://en.wikipedia.org/wiki/Outlier Outlier]), которые могут искажать картину из-за использования среднеквадратичного расстояния: если выбрать <tex>d_{lq}=1/ \| x_l -x_q \|</tex>, то влияние больших уклонений будет уменьшено. Таким образом, описанная модификация метода главных компонент является более [[Робастность в статистике|робастной]], чем классическая. | ||
| + | |||
| + | == Устойчивость главных компонент == | ||
| + | |||
| + | == Анализ соответствий == | ||
| + | |||
| + | [[анализ соответствий|Анализ соответствий]] (англ. [http://www.statsoft.com/textbook/stcoran.html Correspondence analysis])... | ||
| + | |||
| + | == Специальная терминология == | ||
| + | |||
| + | В статистике при использовании метода главных компонент используют несколько специальных терминов. | ||
| + | |||
| + | '''Матрица данных''' <tex>\mathbf{X}=\{x_1,... x_m\}^T</tex>; каждая строка — вектор ''предобработанных'' данных (''центрированных'' и правильно ''нормированных''), число строк — <tex>m</tex> (количество векторов данных), число столбцов — <tex>n</tex> (размерность пространства данных); | ||
| + | |||
| + | '''Матрица нагрузок''' (Loadings) <tex>\mathbf{P}=\{a_1,... a_k\}</tex>; каждый столбец — вектор главных компонент, число строк — <tex>n</tex> (размерность пространства данных), число столбцов — <tex>k</tex> (количество векторов главных компонент, выбранных для проецирования); | ||
| + | |||
| + | '''Матрица счетов''' (Scores) <tex>\mathbf{T}=[t_{ij}]; \; t_{ij}=(x_i,a_j)</tex>; каждая строка — проекция вектора данных на <tex>k</tex> главных компонент; число строк — <tex>m</tex> (количество векторов данных), число столбцов — <tex>k</tex> (количество векторов главных компонент, выбранных для проецирования); | ||
| + | |||
| + | '''Матрица Z-счетов''' (Z-scores) <tex>\mathbf{Z}=[z_{ij}]; \; z_{ij}=\frac{(x_i,a_j)}{\sqrt{ \lambda_j}}</tex>; каждая строка — проекция вектора данных на <tex>k</tex> главных компонент, нормированная на единичную выборочную дисперсию; число строк — <tex>m</tex> (количество векторов данных), число столбцов — <tex>k</tex> (количество векторов главных компонент, выбранных для проецирования); | ||
| + | |||
| + | '''Матрица ошибок''' (или '''остатков''') (Errors or residuals) <tex>\mathbf{E}=\mathbf{X}-\mathbf{T}\mathbf{P}^T</tex>. | ||
| + | |||
| + | Основная формула: <tex>\mathbf{X}=\mathbf{T}\mathbf{P}^T+\mathbf{E}.</tex> | ||
| + | |||
| + | == Пределы применимости и ограничения эффективности метода == | ||
| + | |||
| + | |||
| + | [[Изображение: BranchingPrincipalComponents.gif|thumb|250px| Построение ветвящихся главных компонент методом топологических грамматик. Крестики — точки данных, красное дерево с желтыми узлами — аппроксимирующий дендрит<ref name="TopGram">Описание метода можно найти в статье: ''Gorban A. N. , Sumner N. R., and Zinovyev A. Y.'', Topological grammars for data approximation, Applied Mathematics Letters, Volume 20, Issue 4 (2007), 382—386; или ''Gorban A. N. , Sumner N. R., and Zinovyev A. Y.'', [http://pca.narod.ru/contentsgkwz.htm Beyond The Concept of Manifolds: Principal Trees, Metro Maps, and Elastic Cubic Complexes] In: Gorban A. N. et al (Eds.), LNCSE 58, Springer, 2007 ISBN 978-3-540-73749-0; [http://arxiv.org/abs/0801.0176 а также в arXiv]</ref>.]] | ||
| + | |||
| + | Метод главных компонент применим всегда. Распространённое утверждение о том, что он применим только к [[Нормальное распределение|нормально распределённым]] данным (или для распределений, близких к нормальным) неверно: в исходной формулировке К. Пирсона ставится задача об ''аппроксимации'' конечного множества данных и отсутствует даже гипотеза о их статистическом порождении, не говоря уж о распределении. | ||
| + | |||
| + | Однако метод не всегда эффективно снижает размерность при заданных ограничениях на точность <tex> \delta_k</tex>. Прямые и плоскости не всегда обеспечивают хорошую аппроксимацию. Например, данные могут с хорошей точностью следовать какой-нибудь кривой, а эта кривая может быть сложно расположена в пространстве данных. В этом случае метод главных компонент для приемлемой точности потребует нескольких компонент (вместо одной), или вообще не даст снижения размерности при приемлемой точности. Для работы с такими «кривыми» главными компонентами изобретен метод главных многообразий<ref>С этой работы началось изучение главных многообразий. Диссертация ''T. Хасти'': ''Hastie T.'', [http://www.slac.stanford.edu/pubs/slacreports/slac-r-276.html Principal Curves and Surfaces], Ph.D Dissertation, Stanford Linear Accelerator Center, Stanford University, Stanford, California, US, November 1984. [http://pca.narod.ru/HastieThesis.htm А также на сайте PCA]</ref> и различные версии нелинейного метода главных компонент<ref>''Scholz M., Fraunholz M., Selbig J.'', [http://pca.narod.ru/contentsgkwz.htm Nonlinear Principal Component Analysis: Neural Network Models and Applications], In: Gorban A. N. et al (Eds.), LNCSE 58, Springer, 2007 ISBN 978-3-540-73749-0</ref><ref>''Yin H.'' [http://pca.narod.ru/contentsgkwz.htm Learning Nonlinear Principal Manifolds by Self-Organising Maps], In: Gorban A. N. et al (Eds.), LNCSE 58, Springer, 2007 ISBN 978-3-540-73749-0</ref>. Больше неприятностей могут доставить данные сложной топологии. Для их аппроксимации также изобретены различные методы, например [[Самоорганизующаяся карта Кохонена|самоорганизующиеся карты Кохонена]], [[нейронный газ]]<ref>''Martinetz, T.M., Berkovich, S.G., and Schulten K.J.'', [http://pca.narod.ru/MartinesShultenNeuralGas1993.pdf Neural-gas network for vector quantization and its application to time-series prediction.] IEEE Transactions on Neural Networks, 4 (1993) #4, 558—569. На сайте [http://pca.narod.ru/ PCA]</ref> или топологические грамматики<ref name="TopGram"/>. Если данные статистически порождены с распределением, сильно отличающимся от нормального, то для аппроксимации распределения полезно перейти от главных компонент к ''независимым компонентам''<ref>''Hyvdrinen A, Karhunen J., and Oja E.'', Independent Component Analysis, A Volume in the Wiley Series on Adaptive and Learning Systems for Signal Processing, Communications, and Control. — John Wiley & Sons, Inc., 2001. — XVI+481 pp. ISBN 0-471-40540-X</ref>, которые уже не ортогональны в исходном скалярном произведении. Наконец, для изотропного распределения (даже нормального) вместо эллипсоида рассеяния получаем шар, и уменьшить размерность методами аппроксимации невозможно. | ||
| + | |||
| + | == Примеры использования == | ||
| + | |||
| + | {{main|Применение метода главных компонент}} | ||
| + | |||
| + | Метод главных компонент — наиболее популярный метод сокращения размерности во многих приложениях, в том числе в следующих областях: | ||
| + | * Визуализация данных; | ||
| + | * Компрессия изображений и видео; | ||
| + | * Подавление шума на изображениях; | ||
| + | * Индексация видео; | ||
| + | * Биоинформатика; | ||
| + | * Хемометрика; | ||
| + | * Психодиагностика; | ||
| + | * Общественные науки (включая политологию); | ||
| + | * Сокращение размерности динамических моделей (в том числе — в вычислительной гидродинамике). | ||
== Литература == | == Литература == | ||
| - | |||
| - | |||
| - | |||
| - | |||
| - | == | + | === Классические работы === |
| - | * [http://pca.narod.ru/ Нелинейный метод главных компонент] | + | |
| + | * ''Pearson K.'', On lines and planes of closest fit to systems of points in space, Philosophical Magazine, (1901) 2, 559—572; [http://pca.narod.ru/ а также на сайте PCA]. | ||
| + | * ''Sylvester J.J.'', On the reduction of a bilinear quantic of the nth order to the form of a sum of n products by a double orthogonal substitution, Messenger of Mathematics, 19 (1889), 42—46; [http://pca.narod.ru/ а также на сайте PCA]. | ||
| + | * ''Frećhet M. '' Les élements aléatoires de nature quelconque dans un espace distancié. Ann. Inst. H. Poincaré, 10 (1948), 215—310. | ||
| + | |||
| + | === Основные руководства (стандарт де-факто) === | ||
| + | |||
| + | * ''Айвазян С. А., Бухштабер В. М., Енюков И. С., Мешалкин Л. Д.'' Прикладная статистика. Классификация и снижение размерности.— М.: Финансы и статистика, 1989.— 607 с. | ||
| + | * ''Рао С. Р.'', Линейные статистические методы и их применения.— М.: Наука (Физматлит), 1968.— 548 с. | ||
| + | * ''Jolliffe I.T.'' [http://www.springer.com/statistics/statistical+theory+and+methods/book/978-0-387-95442-4 Principal Component Analysis], Series: [http://www.springer.com/series/692 Springer Series in Statistics], 2nd ed., Springer, NY, 2002, XXIX, 487 p. 28 illus. ISBN 978-0-387-95442-4 | ||
| + | |||
| + | === Сборник современных обзоров === | ||
| + | |||
| + | * ''Gorban A. N., Kegl B., Wunsch D., Zinovyev A. Y.'' (Eds.), [http://www.springer.com/west/home/math/cse?SGWID=4-10045-22-173750210-0 Principal Manifolds for Data Visualisation and Dimension Reduction], [http://www.springer.com/west/home/math/cse?SGWID=4-10045-69-173622682-0 Series: Lecture Notes in Computational Science and Engineering] 58, Springer, Berlin — Heidelberg — New York, 2008, XXIV, 340 p. 82 illus. ISBN 978-3-540-73749-0 (а также [http://pca.narod.ru/ онлайн]). | ||
| + | |||
| + | == Ссылки == | ||
| + | |||
| + | * [http://www.snl.salk.edu/~shlens/pub/notes/pca.pdf A tutorial on Principal Components Analysis], Jonathon Shlens, 22, 2009; Version 3.01. | ||
| + | * [http://pca.narod.ru Нелинейный метод главных компонент] (сайт-библиотека) | ||
| + | * [http://ru.wikipedia.org/wiki/Метод_главных_компонент Метод главных компонент на wikipedia.org] | ||
| + | |||
| + | == Учебное програмное обеспечение == | ||
| + | |||
| + | Java-апплет «Метод главных компонент и самоорганизующиеся карты» (E.M. Mirkes, [http://www.math.le.ac.uk/people/ag153/homepage/PCA_SOM/PCA_SOM.html Principal Component Analysis and Self-Organizing Maps: applet]. University of Leicester, 2011). Свободно распространяемая программа с моделями метода главных компонент, [[Самоорганизующаяся карта Кохонена|самоорганизуюшихся карт]] (SOM) и растущих самоорганизующихся карт (Growing Self-Organized Maps, GSOM). Дано описание алгоритмов (англ.), приведены тьюториалы и некоторые публикации. Используется для выполнения небольших студенческих исследовательских работ по сравнению различных алгоритмов аппроксимации данных. | ||
| + | |||
| + | == Примечания == | ||
| + | <references/> | ||
| - | + | ''Незарегистрированные пользователи не видят примечаний и основных литературных ссылок (дефект системы). Зарегистрироваться безопасно и просто.'' | |
| + | [[Категория:Метод главных компонент]] | ||
[[Категория:Регрессионный анализ]] | [[Категория:Регрессионный анализ]] | ||
[[Категория:Интеллектуальный анализ данных]] | [[Категория:Интеллектуальный анализ данных]] | ||
[[Категория:Машинное обучение]] | [[Категория:Машинное обучение]] | ||
[[Категория:Энциклопедия анализа данных]] | [[Категория:Энциклопедия анализа данных]] | ||
| + | [[Категория:Популярные и обзорные статьи]] | ||
Текущая версия
Метод Главных Компонент (англ. Principal Components Analysis, PCA) — один из основных способов уменьшить размерность данных, потеряв наименьшее количество информации. Изобретен К. Пирсоном (англ.Karl Pearson) в 1901 г. Применяется во многих областях, таких как распознавание образов, компьютерное зрение, сжатие данных и т. п. Вычисление главных компонент сводится к вычислению собственных векторов и собственных значений ковариационной матрицы исходных данных или к сингулярному разложению матрицы данных. Иногда метод главных компонент называют преобразованием Кархунена-Лоэва (англ. Karhunen-Loeve)[1] или преобразованием Хотеллинга (англ. Hotelling transform). Другие способы уменьшения размерности данных — это метод независимых компонент, многомерное шкалирование, а также многочисленные нелинейные обобщения: метод главных кривых и многообразий, поиск наилучшей проекции (англ. Projection Pursuit), нейросетевые методы «узкого горла», самоорганизующиеся карты Кохонена и др.
Формальная постановка задачи
Задача анализа главных компонент, имеет, как минимум, четыре базовых версии:
- аппроксимировать данные линейными многообразиями меньшей размерности;
- найти подпространства меньшей размерности, в ортогональной проекции на которые разброс данных (т.е. среднеквадратичное уклонение от среднего значения) максимален;
- найти подпространства меньшей размерности, в ортогональной проекции на которые среднеквадратичное расстояние между точками максимально;
- для данной многомерной случайной величины построить такое ортогональное преобразование координат, что в результате корреляции между отдельными координатами обратятся в ноль.
Первые три версии оперируют конечными множествами данных. Они эквивалентны и не используют никакой гипотезы о статистическом порождении данных. Четвёртая версия оперирует случайными величинами. Конечные множества появляются здесь как выборки из данного распределения, а решение трёх первых задач — как приближение к «истинному» преобразованию Кархунена-Лоэва. При этом возникает дополнительный и не вполне тривиальный вопрос о точности этого приближения.
Аппроксимация данных линейными многообразиями
Метод главных компонент начинался с задачи наилучшей аппроксимации конечного множества точек прямыми и плоскостями (К. Пирсон, 1901). Дано конечное множество векторов . Для каждого
среди всех
-мерных линейных многообразий в
найти такое
, что сумма квадратов уклонений
от
минимальна:
-
,
где — евклидово расстояние от точки до линейного многообразия. Всякое
-мерное линейное многообразие в
может быть задано как множество линейных комбинаций
, где параметры
пробегают вещественную прямую
,
а
— ортонормированный набор векторов
-
,
где евклидова норма,
— евклидово скалярное произведение, или в координатной форме:
-
.
Решение задачи аппроксимации для даётся набором вложенных линейных многообразий
,
. Эти линейные многообразия определяются ортонормированным набором векторов
(векторами главных компонент) и вектором
.
Вектор
ищется, как решение задачи минимизации для
:
то есть
-
.
Это — выборочное среднее:
Фреше в 1948 году обратил внимание, что вариационное определение среднего (как точки, минимизирующей сумму квадратов расстояний до точек данных) очень удобно для построения статистики в произвольном метрическом пространстве, и построил обобщение классической статистики для общих пространств (обобщённый метод наименьших квадратов).
Векторы главных компонент могут быть найдены как решения однотипных задач оптимизации:
- 1) централизуем данные (вычитаем среднее):
. Теперь
;
- 2) находим первую главную компоненту как решение задачи;
-
.
- Если решение не единственно, то выбираем одно из них.
-
- 3) Вычитаем из данных проекцию на первую главную компоненту:
-
;
-
- 4) находим вторую главную компоненту как решение задачи
-
.
- Если решение не единственно, то выбираем одно из них.
- …
-
- 2k-1) Вычитаем проекцию на
-ю главную компоненту (напомним, что проекции на предшествующие
главные компоненты уже вычтены):
-
;
-
- 2k) находим k-ю главную компоненту как решение задачи:
-
.
- Если решение не единственно, то выбираем одно из них.
- …
-
На каждом подготовительном шаге вычитаем проекцию на предшествующую главную компоненту. Найденные векторы
ортонормированы просто в результате решения описанной задачи оптимизации, однако чтобы не дать ошибкам вычисления нарушить взаимную ортогональность векторов главных компонент, можно включать
в условия задачи оптимизации.
Неединственность в определении помимо тривиального произвола в выборе знака (
и
решают ту же задачу) может быть более существенной и происходить, например, из условий симметрии данных.
Поиск ортогональных проекций с наибольшим рассеянием
Пусть нам дан центрированный набор векторов данных (среднее арифметическое значение
равно нулю). Задача — найти такое ортогональное преобразование в новую систему координат, для которого были бы верны следующие условия:
- Выборочная дисперсия данных вдоль первой координаты максимальна (эту координату называют первой главной компонентой);
- Выборочная дисперсия данных вдоль второй координаты максимальна при условии ортогональности первой координате (вторая главная компонента);
- …
- Выборочная дисперсия данных вдоль значений
-ой координаты максимальна при условии ортогональности первым
координатам;
- …
Выборочная дисперсия данных вдоль направления, заданного нормированным вектором , это
(поскольку данные центрированы, выборочная дисперсия здесь совпадает со средним квадратом уклонения от нуля).
Формально, если ,
— искомое преобразование, то для векторов
должны выполняться следующие условия:
- Если решение не единственно, то выбираем одно из них.
- Вычитаем из данных проекцию на первую главную компоненту:
-
; в результате
;
- находим вторую главную компоненту как решение задачи
-
- Если решение не единственно, то выбираем одно из них.
- …
- Вычитаем проекцию на
-ю главную компоненту (напомним, что проекции на предшествующие
главные компоненты уже вычтены):
-
; в результате
;
- находим
-ю главную компоненту как решение задачи
-
- Если решение не единственно, то выбираем одно из них.
- ...
Фактически, как и для задачи аппроксимации, на каждом шаге решается задача о первой главной компоненте для данных, из которых вычтены проекции на все ранее найденные главные компоненты. При большом числе итерации (большая размерность, много главных компонент) отклонения от ортогональности накапливаются и может потребоваться специальная коррекция алгоритма или другой алгоритм поиска собственных векторов ковариационной матрицы.
Решение задачи о наилучшей аппроксимации даёт то же множество решений , что и поиск ортогональных проекций с наибольшим рассеянием, по очень простой причине:
и первое слагаемое не зависит от
. Только одно дополнение к задаче об аппроксимации: появляется последняя главная компонента
Поиск ортогональных проекций с наибольшим среднеквадратичным расстоянием между точками
Ещё одна эквивалентная формулировка следует из очевидного тождества, верного для любых векторов
:
В левой части этого тождества стоит среднеквадратичное расстояние между точками, а в квадратных скобках справа — выборочная дисперсия. Таким образом, в методе главных компонент ищутся подпространства, в проекции на которые среднеквадратичное расстояние между точками максимально (или, что то же самое, его искажение в результате проекции минимально)[1]. Такая переформулировка позволяет строить обобщения с взвешиванием различных парных расстояний (а не только точек).
Аннулирование корреляций между координатами
Для заданной -мерной случайной величины
найти такой ортонормированный базис,
, в котором коэффициент ковариации между различными координатами равен нулю. После преобразования к этому базису
-
для
.
Здесь — коэффициент ковариации.
Диагонализация ковариационной матрицы
Все задачи о главных компонентах приводят к задаче диагонализации ковариационной матрицы или выборочной ковариационной матрицы. Эмпирическая или выборочная ковариационная матрица, это
Ковариационная матрица многомерной случайной величины , это
Векторы главных компонент для задач о наилучшей аппроксимации и о поиске ортогональных проекций с наибольшим рассеянием — это ортонормированный набор собственных векторов эмпирической ковариационной матрицы
, расположенных в порядке убывания собственных значений
Эти векторы служат оценкой для собственных векторов ковариационной матрицы
. В базисе из собственных векторов ковариационной матрицы она, естественно, диагональна, и в этом базисе коэффициент ковариации между различными координатами равен нулю.
Если спектр ковариационной матрицы вырожден, то выбирают произвольный ортонормированный базис собственных векторов. Он существует всегда, а собственные числа ковариационной матрицы всегда вещественны и неотрицательны.
Сингулярное разложение матрицы данных
Математическое содержание метода главных компонент — это спектральное разложение ковариационной матрицы , то есть представление пространства данных в виде суммы взаимно ортогональных собственных подпространств
, а самой матрицы
— в виде линейной комбинации ортогональных проекторов на эти подпространства с коэффициентами
. Если
— матрица, составленная из векторов-строк центрированных данных, то
и задача о спектральном разложении ковариационной матрицы
превращается в задачу о сингулярном разложении (англ. Singular value decomposition) матрицы данных
.
Хотя формально задачи сингулярного разложения матрицы данных и спектрального разложения ковариационной матрицы совпадают, алгоритмы вычисления сингулярного разложения напрямую, без вычисления ковариационной матрицы и её спектра, более эффективны и устойчивы [1].
Теория сингулярного разложения была создана Дж. Дж. Сильвестром (англ. J. J. Sylvester) в 1889 г. и изложена во всех подробных руководствах по теории матриц [1].
Матрица преобразования к главным компонентам
Матрица преобразования данных к главным компонентам строится из векторов главных компонент:
. Здесь
— ортонормированные векторы-столбцы главных компонент, расположенные в порядке убывания собственных значений, верхний индекс
означает транспонирование. Матрица
является ортогональной:
.
После преобразования большая часть вариации данных будет сосредоточена в первых координатах, что даёт возможность отбросить оставшиеся и рассмотреть пространство уменьшенной размерности.
Остаточная дисперсия
Пусть данные центрированы, . При замене векторов данных
на их проекцию на первые
главных компонент
вносится средний квадрат ошибки в расчете на один вектор данных:
где собственные значения эмпирической ковариационной матрицы
, расположенные в порядке убывания, с учетом кратности.
Эта величина называется остаточной дисперсией. Величина
называется объяснённой дисперсией. Их сумма равна выборочной дисперсии. Соответствующий квадрат относительной ошибки — это отношение остаточной дисперсии к выборочной дисперсии (то есть доля необъяснённой дисперсии):
По относительной ошибке оценивается применимость метода главных компонент с проецированием на первые
компонент.
Замечание: в большинстве вычислительных алгоритмов собственные числа с соответствуюшими собственными векторами — главными компонентами
вычисляются в порядке «от больших
— к меньшим». Для вычисления
достаточно вычислить первые
собственных чисел и след эмпирической ковариационной матрицы
,
(сумму диагональных элементов
, то есть дисперсий по осям). Тогда
Оценка числа главных компонент по правилу сломанной трости
Целевой подход к оценке числа главных компонент по необходимой доле объяснённой дисперсии формально применим всегда, однако неявно он предполагает, что нет разделения на "сигнал" и "шум", и любая заранее заданная точность имеет смысл. Поэтому часто более продуктивна иная эвристика, основывающаяся на гипотезе о наличии "сигнала" (сравнительно малая размерность, относительно большая амплитуда) и "шума" (большая размерность, относительно малая амплитуда). С этой точки зрения метод главных компонент работает как фильтр: сигнал содержится, в основном, в проекции на первые главные компоненты, а в остальных компонентах пропорция шума намного выше.
Вопрос, как оценить число необходимых главных компонент, если отношение "сигнал/шум" заранее неизвестно? Одним из наиболее популярных эвристических подходов является правило сломанной трости (англ. Broken stick model)[1]. Набор нормированных собственных чисел (,
) сравнивается с распределением длин обломков трости единичной длины, сломанной в
-й случайно выбранной точке (точки разлома выбираются независимо и равнораспределены по длине трости). Пусть
(
) - длины полученных кусков трости, занумерованные в порядке убывания длины:
. Нетрудно найти математическое ожидание
:
По правилу сломанной трости -й собственный вектор (в порядке убывания собственных чисел
) сохраняется в списке главных компонент, если
На Рис. приведён пример для 5-мерного случая:
=(1+1/2+1/3+1/4+1/5)/5;
=(1/2+1/3+1/4+1/5)/5;
=(1/3+1/4+1/5)/5;
=(1/4+1/5)/5;
=(1/5)/5.
Для примера выбрано
=0.5;
=0.3;
=0.1;
=0.06;
=0.04.
По правилу сломанной трости в этом примере следует оставлять 2 главных компоненты:
Нормировка
Нормировка после приведения к главным компонентам
После проецирования на первые главных компонент с
удобно произвести нормировку на единичную (выборочную) дисперсию по осям. Дисперсия вдоль
й главной компоненты равна
), поэтому для нормировки надо разделить соответствующую координату на
. Это преобразование не является ортогональным и не сохраняет скалярного произведения. Ковариационная матрица проекции данных после нормировки становится единичной, проекции на любые два ортогональных направления становятся независимыми величинами, а любой ортонормированный базис становится базисом главных компонент (напомним, что нормировка меняет отношение ортогональности векторов). Отображение из пространства исходных данных на первые
главных компонент вместе с нормировкой задается матрицей
-
.
Именно это преобразование чаще всего называется преобразованием Кархунена-Лоэва. Здесь — векторы-столбцы, а верхний индекс
означает транспонирование.
Нормировка до вычисления главных компонент
Предупреждение: не следует путать нормировку, проводимую после преобразования к главным компонентам, с нормировкой и «обезразмериванием» при предобработке данных, проводимой до вычисления главных компонент. Предварительная нормировка нужна для обоснованного выбора метрики, в которой будет вычисляться наилучшая аппроксимация денных, или будут искаться направления наибольшего разброса (что эквивалентно). Например, если данные представляют собой трёхмерные векторы из «метров, литров и килограмм», то при использовании стандартного евклидового расстояния разница в 1 метр по первой координате будет вносить тот же вклад, что разница в 1 литр по второй, или в 1 кг по третьей. Обычно системы единиц, в которых представлены исходные данные, недостаточно точно отображают наши представления о естественных масштабах по осям, и проводится «обезразмеривание»: каждая координата делится на некоторый масштаб, определяемый данными, целями их обработки и процессами измерения и сбора данных.
Есть три cущественно различных стандартных подхода к такой нормировке: на единичную дисперсию по осям (масштабы по осям равны средним квадратичным уклонениям — после этого преобразования ковариационная матрица совпадает с матрицей коэффициентов корреляции), на равную точность измерения (масштаб по оси пропорционален точности измерения данной величины) и на равные требования в задаче (масштаб по оси определяется требуемой точностью прогноза данной величины или допустимым её искажением — уровнем толерантности). На выбор предобработки влияют содержательная постановка задачи, а также условия сбора данных (например, если коллекция данных принципиально не завершена и данные будут ещё поступать, то нерационально выбирать нормировку строго на единичную дисперсию, даже если это соответствует смыслу задачи, поскольку это предполагает перенормировку всех данных после получения новой порции; разумнее выбрать некоторый масштаб, грубо оценивающий стандартное отклонение, и далее его не менять).
Предварительная нормировка на единичную дисперсию по осям разрушается поворотом системы координат, если оси не являются главными компонентами, и нормировка при предобработке данных не заменяет нормировку после приведения к главным компонентам.
Механическая аналогия и метод главных компонент для взвешенных данных
Если сопоставить каждому вектору данных единичную массу, то эмпирическая ковариационная матрица
совпадёт с тензором инерции этой системы точечных масс (делённым на полную массу
), а задача о главных компонентых — с задачей приведения тензора инерции к главным осям. Можно использовать дополнительную свободу в выборе значений масс для учета важности точек данных или надежности их значений (важным данным или данным из более надежных источников приписываются бо́льшие массы). Если вектору данных
придаётся масса
, то вместо эмпирической ковариационной матрицы
получим
Все дальнейшие операции по приведению к главным компонентам производятся так же, как и в основной версии метода: ищем ортонормированный собственный базис , упорядочиваем его по убыванию собственных значений, оцениваем средневзвешенную ошибку аппроксимации данных первыми
компонентами (по суммам собственных чисел
), нормируем и т. п.
Более общий способ взвешивания даёт максимизация взвешенной суммы попарных расстояний[1] между проекциями. Для каждых двух точек данных, вводится вес
;
и
. Вместо эмпирической ковариационной матрицы
используется
При симметричная матрица
положительно определена, поскольку положительна квадратичная форма:
Далее ищем ортонормированный собственный базис , упорядочиваем его по убыванию собственных значений, оцениваем средневзвешенную ошибку аппроксимации данных первыми
компонентами и т. д. — в точности так же, как и в основном алгоритме.
Этот способ применяется при наличии классов: для из разных классов вес
вес выбирается бо́льшим, чем для точек одного класса. В результате, в проекции на взвешенные главные компоненты различные классы «раздвигаются» на большее расстояние.
Другое применение — снижение влияния больших уклонений (оутлайеров, англ.Outlier), которые могут искажать картину из-за использования среднеквадратичного расстояния: если выбрать , то влияние больших уклонений будет уменьшено. Таким образом, описанная модификация метода главных компонент является более робастной, чем классическая.
Устойчивость главных компонент
Анализ соответствий
Анализ соответствий (англ. Correspondence analysis)...
Специальная терминология
В статистике при использовании метода главных компонент используют несколько специальных терминов.
Матрица данных ; каждая строка — вектор предобработанных данных (центрированных и правильно нормированных), число строк —
(количество векторов данных), число столбцов —
(размерность пространства данных);
Матрица нагрузок (Loadings) ; каждый столбец — вектор главных компонент, число строк —
(размерность пространства данных), число столбцов —
(количество векторов главных компонент, выбранных для проецирования);
Матрица счетов (Scores) ; каждая строка — проекция вектора данных на
главных компонент; число строк —
(количество векторов данных), число столбцов —
(количество векторов главных компонент, выбранных для проецирования);
Матрица Z-счетов (Z-scores) ; каждая строка — проекция вектора данных на
главных компонент, нормированная на единичную выборочную дисперсию; число строк —
(количество векторов данных), число столбцов —
(количество векторов главных компонент, выбранных для проецирования);
Матрица ошибок (или остатков) (Errors or residuals) .
Основная формула:
Пределы применимости и ограничения эффективности метода
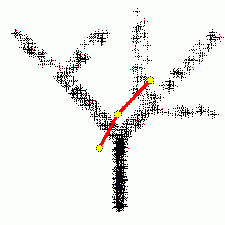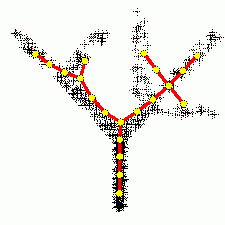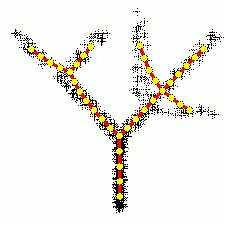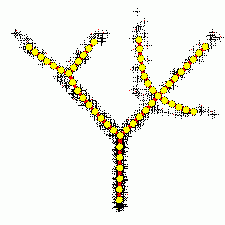
Метод главных компонент применим всегда. Распространённое утверждение о том, что он применим только к нормально распределённым данным (или для распределений, близких к нормальным) неверно: в исходной формулировке К. Пирсона ставится задача об аппроксимации конечного множества данных и отсутствует даже гипотеза о их статистическом порождении, не говоря уж о распределении.
Однако метод не всегда эффективно снижает размерность при заданных ограничениях на точность . Прямые и плоскости не всегда обеспечивают хорошую аппроксимацию. Например, данные могут с хорошей точностью следовать какой-нибудь кривой, а эта кривая может быть сложно расположена в пространстве данных. В этом случае метод главных компонент для приемлемой точности потребует нескольких компонент (вместо одной), или вообще не даст снижения размерности при приемлемой точности. Для работы с такими «кривыми» главными компонентами изобретен метод главных многообразий[1] и различные версии нелинейного метода главных компонент[1][1]. Больше неприятностей могут доставить данные сложной топологии. Для их аппроксимации также изобретены различные методы, например самоорганизующиеся карты Кохонена, нейронный газ[1] или топологические грамматики[1]. Если данные статистически порождены с распределением, сильно отличающимся от нормального, то для аппроксимации распределения полезно перейти от главных компонент к независимым компонентам[1], которые уже не ортогональны в исходном скалярном произведении. Наконец, для изотропного распределения (даже нормального) вместо эллипсоида рассеяния получаем шар, и уменьшить размерность методами аппроксимации невозможно.
Примеры использования
Метод главных компонент — наиболее популярный метод сокращения размерности во многих приложениях, в том числе в следующих областях:
- Визуализация данных;
- Компрессия изображений и видео;
- Подавление шума на изображениях;
- Индексация видео;
- Биоинформатика;
- Хемометрика;
- Психодиагностика;
- Общественные науки (включая политологию);
- Сокращение размерности динамических моделей (в том числе — в вычислительной гидродинамике).
Литература
Классические работы
- Pearson K., On lines and planes of closest fit to systems of points in space, Philosophical Magazine, (1901) 2, 559—572; а также на сайте PCA.
- Sylvester J.J., On the reduction of a bilinear quantic of the nth order to the form of a sum of n products by a double orthogonal substitution, Messenger of Mathematics, 19 (1889), 42—46; а также на сайте PCA.
- Frećhet M. Les élements aléatoires de nature quelconque dans un espace distancié. Ann. Inst. H. Poincaré, 10 (1948), 215—310.
Основные руководства (стандарт де-факто)
- Айвазян С. А., Бухштабер В. М., Енюков И. С., Мешалкин Л. Д. Прикладная статистика. Классификация и снижение размерности.— М.: Финансы и статистика, 1989.— 607 с.
- Рао С. Р., Линейные статистические методы и их применения.— М.: Наука (Физматлит), 1968.— 548 с.
- Jolliffe I.T. Principal Component Analysis, Series: Springer Series in Statistics, 2nd ed., Springer, NY, 2002, XXIX, 487 p. 28 illus. ISBN 978-0-387-95442-4
Сборник современных обзоров
- Gorban A. N., Kegl B., Wunsch D., Zinovyev A. Y. (Eds.), Principal Manifolds for Data Visualisation and Dimension Reduction, Series: Lecture Notes in Computational Science and Engineering 58, Springer, Berlin — Heidelberg — New York, 2008, XXIV, 340 p. 82 illus. ISBN 978-3-540-73749-0 (а также онлайн).
Ссылки
- A tutorial on Principal Components Analysis, Jonathon Shlens, 22, 2009; Version 3.01.
- Нелинейный метод главных компонент (сайт-библиотека)
- Метод главных компонент на wikipedia.org
Учебное програмное обеспечение
Java-апплет «Метод главных компонент и самоорганизующиеся карты» (E.M. Mirkes, Principal Component Analysis and Self-Organizing Maps: applet. University of Leicester, 2011). Свободно распространяемая программа с моделями метода главных компонент, самоорганизуюшихся карт (SOM) и растущих самоорганизующихся карт (Growing Self-Organized Maps, GSOM). Дано описание алгоритмов (англ.), приведены тьюториалы и некоторые публикации. Используется для выполнения небольших студенческих исследовательских работ по сравнению различных алгоритмов аппроксимации данных.
Примечания
Незарегистрированные пользователи не видят примечаний и основных литературных ссылок (дефект системы). Зарегистрироваться безопасно и просто.