Метод релевантных векторов

Материал из MachineLearning.

(Различия между версиями)

Текущая версия

Метод релевантных векторов (RVM, Relevance vector machine) — алгоритм классификации и восстановления регрессии, основанный на байесовском выводе второго уровня. В методе используется обобщенная линейная модель с введенной регуляризацией, которая, в Байесовкой интерпретации, равносильна введению априорных распределений на вектор параметров. Главной особенностью является то, что все параметры регуляризируются независимо.

Решаемая задача

Имеется выборка $\left(X,t\right) = \left{ \mathbf{x}_i ,t_i \right}^l_{i=1}$ , где вектор признаков $\mathbf{x}_i \in \mathbb{R}^m$ , а целевая переменная $t_i \in \mathbb {R}$ . Требуется для нового объекта $\mathbf{x}_*$ предсказать значение целевой переменной $t_*$
Предполагается, что $t=f(\mathbf{x})+\varepsilon$ , где $\varepsilon \sim \mathfrak{N}(\varepsilon|0,\sigma^2)$ , а

$f(\mathbf{x}) = \sum_{j=1}^m \omega_j\phi_j(\mathbf{x}) = \mathbf{\omega}^T\mathbf{\phi}(\mathbf{x})$

Подход к решению

Следуя байесовскому подходу, воспользуемся методом максимума апостериорной плотности:

$\mathbf{\omega}_{MP} = \arg\,\max_{\mathbf{\omega}}\,\,p(\mathbf{\omega} |X,\mathbf{t}) = \arg\,\max_{\mathbf{\omega}} \,\,p(\mathbf{t} |X,\mathbf{\omega}) p(\mathbf{\omega})$

Для получения разреженного решения введем в качестве априорного распределения на параметры $\mathbf{\omega}$ нормальное распределение с диагональной матрицей ковариации с различными элементами на диагонали:

$p(\mathbf{\omega} |\mathbf{\alpha}) = \mathfrak{N}(0,A^{-1})$

Здесь $A=\mbox{diag}\,(\alpha_1,\ldots,\alpha_m)$ . Такое априорное распределение соответствует независимой регуляризации вдоль каждого веса $\omega_i$ со своим параметром регуляризации $\alpha_i \ge 0$

Для обучения модели (настройки параметров $\mathbf{\omega} ,\sigma$ ) воспользуемся идеей максимизации обоснованности:

$p(\mathbf{t} |X,\mathbf{\alpha} ,\sigma^2) = \int p(\mathbf{t} |X,\mathbf{\omega}, \sigma^2)p(\mathbf{\omega} |\mathbf{\alpha} )d\mathbf{\omega} \to \max_{\mathbf{\alpha}, \sigma^2}$

Оптимизация обоснованности

Заметив, что обоснованность является сверткой двух нормальных распределений, можно представить подынтегральную функцию по формуле Тейлора в точке максимума правдоподобия. Обозначив $Q(\mathbf{\omega}) = p(\mathbf{t} |X,\mathbf{\omega}, \sigma^2)p(\mathbf{\omega} |\mathbf{\alpha} ) \mbox{, } H = \bigtriangledown\bigtriangledown\,\log Q(\mathbf{\omega}_{MP})$ , после некоторых преобразований получим:

$\int Q( \mathbf{\omega} )d\mathbf{\omega} = \sqrt{\left(2\pi\right)^m}\frac{Q(\mathbf{\omega} _{MP})}{\sqrt{\det(-H)}}$

Обозначив, для удобства, $\beta=\sigma^{-2}$ , и "в лоб" раскрывая предыдущее выражение, получим:

$p(\mathbf{t} |X,\mathbf{\alpha} ,\sigma^2) = \frac{1}{\sqrt{\left(2\pi\right)^m \det\left(\beta^{-1}I+\Phi A ^{-1}\Phi^T \right) }}\exp\left( -\frac{1}{2}\mathbf{t}^T \left( \beta^{-1} I + \Phi A ^{-1} \Phi^T \right)^{-1} \mathbf{t} \right)$ ,

где $\Phi$ — матрица обобщенных признаков.

Теперь, приравнивая нулю производные обоснованности по $\mathbf{\alpha},\,\beta$ , получим итерационные формулы для пересчета параметров:

$\alpha_i^{new} = \frac{\gamma_i}{\omega^2_{MP,i}$

$\gamma_i = \alpha_i^{old}\Sigma_{ii}$

$\beta_i^{new} = \frac{\textstyle{n-\sum_{i=1}^m\gamma_i}}{{\left\parallel \mathbf{t} - \Phi\mathbf{\omega} \right\parallel}^2}{\omega^2_{MP,i}$

Здесь $\Sigma = \left( \beta\Phi^T\Phi+A\right)^{-1}\mbox{, }\; \mathbf{\omega}_{MP} = \beta\Sigma\Phi^T\mathbf{t}$

Параметр $\gamma_i$ можно интерпретировать как степень, в которой соответствующий вес $\omega_i$ определяется данными или регуляризацией. Если $\alpha_i$ велико, то вес $\omega_i$ существенно предопределен априорным распределением, $\textstyle \Sigma_{ii} \simeq \alpha_i^{-1}$ и $\gamma_i \simeq 0$ . С другой стороны, для малых значений $\alpha_i$ значение веса $\omega_i$ полностью определяется данными, $\gamma_i \simeq 0$ .

Принятие решения

Зная значения $\mathbf{\alpha}_{MP},\,\sigma^2_{MP}$ можно вычислить апостериорное распределение целевой переменной:

$p(t_* |\mathbf{x}_*, X) = \int p(t_* |\mathbf{x}_*, \mathbf{\omega}, \sigma^2_{MP})p(\mathbf{\omega} |X, \mathbf{\alpha}_{MP}, \sigma^2_{MP})d\mathbf{\omega} = \mathfrak{N}(t_*|\mathbf{\omega}^T_{MP} \mathbf{\phi}(\mathbf{x}_*),\,\sigma^2_{MP} + \mathbf{\phi}(\mathbf{x}_*)^T \Sigma \mathbf{\phi}(\mathbf{x}_*))$

Обсуждение метода

Пример работы регрессии релевантных векторов для зашумленной функции sinc(x). Объекты, отвечающие релевантным базисным функциям, обведены

На практике процесс обучения обычно требует 20-50 итераций. На каждой итерации вычисляется $\mathbf{\omega}_{MP}$ (это требует обращения матрицы порядка $m\times m$ ), а также пересчитываются значения $\mathbf{\alpha},\,\beta$ (пратктически не требует времени). Как следствие, скорость обучения падает примерно в 20-50 раз по сравнению с линейной регрессией.
При использовании ядровых функций в качестве обобщенных признаков необходимо проводить скользящий контроль для различных значений параметров ядра. В этом случае время обучения возрастает еще в несколько раз.
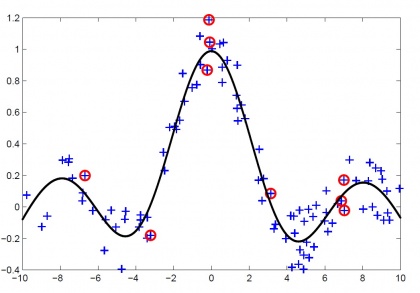
На выходе алгоритма получается разреженное решение, т. е. только небольшое подмножество исходной выборки входит в решающее правило.
Кроме значения целевой переменной, алгоритм выдает также и дисперсию прогноза.

Псевдокод алгоритма RVM

Вход: Обучающая выборка $\left{ \mathbf{x}_i ,t_i \right}^l_{i=1}$ , матрица обобщенных признаков $\Phi = \left{ \phi_j(\mathbf{x}_j) \right}^{n,m}_{i,j=1}$
Выход: Параметры решающего правила: $\mathbf{\omega},\,\Sigma,\,\beta$

Инициализация: $\alpha_i\,:=\,1;\;\beta\,:=\,1;\;\mathtt{AlphaBound}\,:=\,10^{12};\; \mathtt{WeightBound}\,:=\,10^{-6};\; \mathtt{NumberOfIterations}\,:=\,50;$

для $k=1,\ldots,\mathtt{NumberOfIterations}$ повторять

$A\,:=\,\mbox{diag}(\alpha_1,\ldots,\alpha_m);$

$\Sigma\,:=\,\left( \beta\Phi^T\Phi+A \right)^{-1};$

$\mathbf{\omega}_{MP}\,:=\,\Sigma\beta\Phi^T \mathbf{t};$

для $j=1,\ldots,m$ повторять

если $\omega_{MP,j}\, <\, \mathtt{WeightBound}$ или $\alpha_j\, > \,\mathtt{AlphaBound}$ , то

$\omega_{MP,j}\,:=\,0;\,\,\alpha_j\,:=\,+\infty;\,\,\gamma_j\,:=\,0;$

иначе

$\gamma_j\,:=\,\alpha_j^{old}\Sigma_{jj};\,\,\alpha_j\,:=\,\frac{\gamma_j}{\omega^2_{MP,j}$ $;$

$\beta_i\,:=\,\frac{\textstyle{n-\sum_{i=1}^m\gamma_i}}{{\left\parallel \mathbf{t} - \Phi\mathbf{\omega} \right\parallel}^2}{\omega^2_{MP,i}\,;$

См. также

Литература

Tipping M. The relevance vector machine // Advances in Neural Information Processing Systems, San Mateo, CA. — Morgan Kaufmann, 2000.

Данная статья была создана в рамках учебного задания.

Студент: Участник:Dimaleks

Преподаватель: Участник:Константин Воронцов

Срок: 7 января 2009, а сейчас 22 ноября 2024

В настоящее время задание завершено и проверено. Данная страница может свободно правиться другими участниками проекта MachineLearning.ru.

См. также методические указания по использованию Ресурса MachineLearning.ru в учебном процессе.

Источник — «http://machinelearning.ru/wiki/index.php?title=%D0%9C%D0%B5%D1%82%D0%BE%D0%B4_%D1%80%D0%B5%D0%BB%D0%B5%D0%B2%D0%B0%D0%BD%D1%82%D0%BD%D1%8B%D1%85_%D0%B2%D0%B5%D0%BA%D1%82%D0%BE%D1%80%D0%BE%D0%B2»

Категории: Байесовские методы | Линейные классификаторы | Регрессионный анализ

@@ Строка 1: / Строка 1: @@
-'''Метод релевантных векторов (RVM, Relevance vector machine)''' — алгоритм [[классификация|классификации]] и восстановления [[регрессия|регрессии]], основанный на [[байесовский вывод второго уровня|байесовском выводе второго уровня]]. В методе используется [[обобщенная линейная модель]] с введенной [[регуляризация|регуляризацией]], которая, в Байесовкой интерпретации, равносильна введению априорных распределений на вектор параметров. Главной особенностью является то, что все параметры регуляризируются независимо.
+'''Метод релевантных векторов (RVM, Relevance vector machine)''' — алгоритм [[классификация|классификации]] и восстановления [[регрессия|регрессии]], основанный на [[Связанный Байесовский вывод|байесовском выводе второго уровня]]. В методе используется [[обобщенная линейная модель]] с введенной [[регуляризация|регуляризацией]], которая, в Байесовкой интерпретации, равносильна введению априорных распределений на вектор параметров. Главной особенностью является то, что все параметры регуляризируются независимо.
 == Решаемая задача ==
@@ Строка 88: / Строка 88: @@
 [[Категория:Байесовские методы]]
 [[Категория:Линейные классификаторы]]
-[[Категория:Регрессия]]
+[[Категория:Регрессионный анализ]]